神经网络在风烟系统含氧量软测量中的应用
2019-04-08马良玉左晓桐王永军
马良玉,左晓桐,王永军
(华北电力大学控制与计算机工程学院,河北 保定 071003)
0 引言
火力发电厂中,锅炉燃烧状态的优劣直接影响机组煤耗。锅炉燃烧过程中,空气过剩系数α直接反映风煤比,间接反映燃烧是否处于最佳状态。因此,烟气含氧量是影响锅炉燃烧效率的一个重要参数[1]。传统火力发电厂大多采用氧化锆氧量分析仪、热磁式氧量分析仪测量烟气含氧量。但这些仪表测量精度低,维护成本高且使用寿命短,不利于实现长期实时监控。近年来,在过程控制和检测领域出现了一种间接测量参数的软测量技术,有效地解决了传统测量方法存在的问题[2]。本文以某1 000 MW锅炉机组的大量历史运行数据为样本,建立了基于反向传播(back propagation,BP)神经网络的烟气含氧量软测量模型,并通过仿真对比验证了该模型的精度,能够较准确地对氧量进行实时预测。
1 软测量技术
软测量作为一种新型的参数检测技术,为解决复杂工业过程的参数检测提供了一条有效的途径。近年来,软测量技术发展迅速,在理论研究和实际应用方面都取得了显著的成效。软测量模型是软测量技术的核心,它构建了易测过程变量(常称为辅助变量或二次变量)与难以直接测量的待测过程变量(常称为主导变量)之间的数学模型[2]。依据该模型,利用相关软件实现对待测变量的实时测量或估计。
目前,烟气含氧量的软测量方法主要有基于工艺机理分析的方法、基于过程对象动态数学模型的方法、基于人工神经网络的软测量建模方法和基于支持向量机回归的软测量方法[3]。
基于人工神经网络(artificial neural network,ANN)的软测量是过程控制领域发展快、研究多、应用广泛的一种软测量技术。它具有大规模并行处理能力、分布式存储能力、自适应能力以及适用于求解非线性、容错性和冗余性等问题,因而得到迅速发展[4],为解决复杂系统过程参数软测量提供了一种行之有效的方法。近年来,人工神经网络在建立软测量模型方面呈现出很大优势,有着广阔的应用前景。
2 BP神经网络及训练算法
2.1 BP神经网络
人工神经网络是一种对生物神经网络结构和功能进行某种模拟和简化而成的数学模型,其基本组成单位是神经元。BP神经网络是目前应用最为广泛和成熟的神经网络之一。典型的3层BP神经网络结构如图1所示。
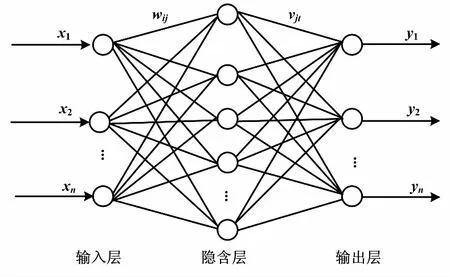
图1 3层BP神经网络结构图Fig.1 Three-layer BP neural network structure
BP神经网络是一个包含输入层、隐含层和输出层3层结构的多层前馈型神经网络,层与层之间通过权值连接,每层各个神经元之间相互独立、互不影响。网络学习过程包括信号的前向传播和误差的反向传播。采用梯度下降法,通过误差的反向传播及修正误差的方向不断调整各层权值和阈值,以期达到输出数据与期望数据的误差性能函数最小的目的[5-7]。
BP神经网络的权值和阈值包括隐含层与输出层神经元之间的权值Vjt、输出层的阈值γt以及隐含层与输入层神经元之间的权值Wij、隐含层的阈值θj,它们分别按照式(1)~式(4)进行调整。
输出层权值:
(1)
输出层阈值:
(2)
隐含层权值:
(3)
隐含层阈值:
(4)

上述误差反向传播算法作为神经网络训练的基本算法,存在收敛速度慢、容易陷入局部最小以及出现“过拟合”等问题。为克服BP神经网络的这些不足,相关研究人员提出了许多改进算法,例如附加动量法、牛顿法、自适应学习率法以及Levenberg-Marquardt(L-M)算法等[8]。
L-M算法在使用时不需要过多调整参数,具有较快的网络收敛速度和较高的网络训练精度。因此,本文采用L-M算法对神经网络进行训练。
2.2 L-M算法
L-M算法是一种求解非线性最小二乘问题的有效方法,它是改进的高斯-牛顿法,既有牛顿法的局部收敛性,又有梯度下降法的全局搜索特性,从而使网络能够有效收敛[9]。其基本原理如下所述[10-11]。
将BP神经网络各层权值和阈值用向量W表示,输出结果的误差性能函数如式(5)所示。
(5)
式中:ei(W)为误差;M为训练样本数。
设e(W)=[e1(W),e2(W),…,ei(W)]T,则:
ΔE(W)=JT(W)e(W)
(6)
式中:ΔE(W)为E(W)的梯度;J(W)为Jacobian矩阵。
(7)
式中:M为训练样本数;N为神经网络权值和阈值的个数。
对于L-M算法,网络权值和阈值的变化ΔWk为:
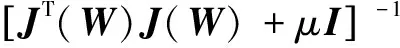
(8)
新的权值和阈值W为:
Wk+1=Wk+ΔWk
(9)
式中:I为单位矩阵;μ为常量系数。
当μ=0时,上式就变成了高斯-牛顿法;当μ值较大时,近似于梯度下降法。在迭代过程中,μ是一个变化的参数。对于给定的μ初始值,如果ΔWk可以使误差性能函数E(W)下降,则减小μ值;反之则增加μ值[6]。
L-M算法优化的BP神经网络实现步骤如下[11]。
①初始化网络的权值阈值,给定训练误差限定值ε、常量系数的初值μ0。令迭代次数k=0,μ=μ0。
②计算误差性能函数E(Wk)。
③如果E(Wk)≤ε,算法收敛,转到步骤⑧;否则转到步骤④。
④依据式(7)计算Jacobian矩阵J(Wk)。
⑤依据式(8)计算ΔWk。
⑥依据式(9)计算新的权值和阈值Wk+1,并以其计算误差性能函数E(Wk+1)。
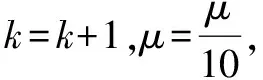
⑧算法结束。
3 1 000 MW火电机组烟气含氧量软测量模型
3.1 辅助变量选取
火电厂测量变量的类型、数目、测点的位置繁多且复杂,测量数据冗余且相关性强,因此需要对辅助变量进行选择。合理选择辅助变量不仅可以增强软测量的精度,而且还可以简化软测量模型,便于理解。影响风烟系统烟气含氧量的因素有很多,选择辅助变量的主要依据是对过程机理的分析。为了保证预测的精确性,应从可测变量中选取相关性强的信息变量。风烟系统烟气含氧量神经网络模型中的辅助变量要选择对烟气含氧量有直接或间接关系的可实时检测变量[12]。结合风烟系统的结构以及各变量参数之间的影响关系,确定网络模型的7个输入参数和1个输出参数。模型输入、输出参数如表1所示。

表1 模型输入、输出参数Tab.1 Model input and output parameters
3.2 数据的采集与处理
本研究采用的数据源自某1 000 MW超临界燃煤机组真实的分散控制系统(distributed control system,DCS)历史数据库。由于数据量巨大,因此依据负荷涵盖范围宽、氧量变化范围大等原则对原始数据进行一定的优选,最终选定了时间间隔为5 s的69 120组数据。以60 s为采样时间,均匀选取5 760组数据作为神经网络的训练样本完成模型的训练,随后从69 120组原始数据中按照一定的规则抽取若干数据段作为模型的测试样本。
从DCS中获取的数据由于有着不同的工程单位,各变量的大小在数值上相差几个数量级。为了预防因不同数据数量级相差较大而造成模型训练时各变量作用差异大,影响模型精度和泛化性能,需要提前对测量数据进行归一化处理,即进行适当的标度变换,将所有的数据都转换为[-1,1]之间的数。本文采用的归一化的公式为:
(10)
式中:y为原始数据x经过归一化后的数据;xmax和xmin分别为所有样本中x的最大值和最小值;ymax和ymin分别为归一化后的最大和最小值,本文分别选用1和-1。
采用归一化后的数据构建网络模型,最终得到的输出结果需要进行反归一化,这样才能得到实际工程单位的烟气含氧量[13]。
3.3 隐含层和初始权值阈值的确定
BP神经网络的设计主要包括输入层、隐含层以及输出层传递函数和节点数的确定。本文隐含层节点传递函数采用非对称型S函数,输出层节点传递函数采用线性函数。输入层和输出层节点数可分别确定为6和1,因此整个网络结构中只有隐含层节点数还有待确定。
目前,关于隐含层节点数并没有准确的确定方法。隐含层节点数对BP神经网络性能影响较大。若节点数过少,则网络不能充分描述输入参数和输出参数之间的关系;若节点数过多,则会延长网络学习时间,甚至出现“过拟合”现象。因此,通过试验,选用均方误差和决定系数作为评价指标[14],对比不同节点数对网络性能的影响,从而确定隐含层节点数。其计算公式分别如式(11)、式(12)。均方误差(mean square error,MSE)和决定系数R2的计算式为:
(11)
(12)

其中,均方误差越小,表示模型的性能越好。决定系数又称拟合优度,其数值在[0,1]之间,决定了曲线的相关程度。R2越接近1,表示相关曲线参考价值越高(模型性能好);反之,参考价值越低(模型性能差)。
在基于梯度下降法的神经网络含氧量软测量模型中,以10 000次为训练周期时,隐含层节点数对网络性能的影响如图2所示。从图2可以看出,当隐含层节点数为41时,均方误差最小,决定系数最接近1。因此,隐含层节点数确定为41。
由于风烟系统是复杂的非线性系统,权值和阈值的初始值对于神经网络学习是否能够收敛影响很大。通常情况要求初始权值在经过累加后能够使每个节点的输出值都趋近于零,因此初始权值和阈值一般取[-1,1]之间的随机数。同时,为消除初始权值和阈值的随机性对不同算法下烟气出口含氧量模型的影响,本文选用一组在[-1,1]之间的固定数值作为权值和阈值的初始值。

图2 隐含层节点数对BP神经网络性能的影响Fig.2 Influence of number of nodes in hidden-layer on the performance of BP neural network
4 模型验证与分析
根据上文所述,构建烟气含氧量软测量模型。为了评价不同算法的BP神经网络模型训练效果,分别采用梯度下降法和L-M算法对BP神经网络模型训练并对结果进行对比分析。
对选取的5 760组样本,分别用梯度下降法和改进的L-M算法对BP神经网络[21]进行训练。训练参数的设定值与实际值见表2,模型训练结果如图3所示。由图3可以看出,L-M算法网络模型可以达到期望误差。

表2 训练参数的设定值与实际值Tab.2 Set value and actual value of training parameters

图3 模型训练结果Fig.3 Training result of model
为测试模型的性能,从周期为5 s的69 120组数据中抽取17 280组作为测试样本,采用相对误差这个指标对软测量模型性能进行评价。测试结果对比与相对误差曲线如图4所示。
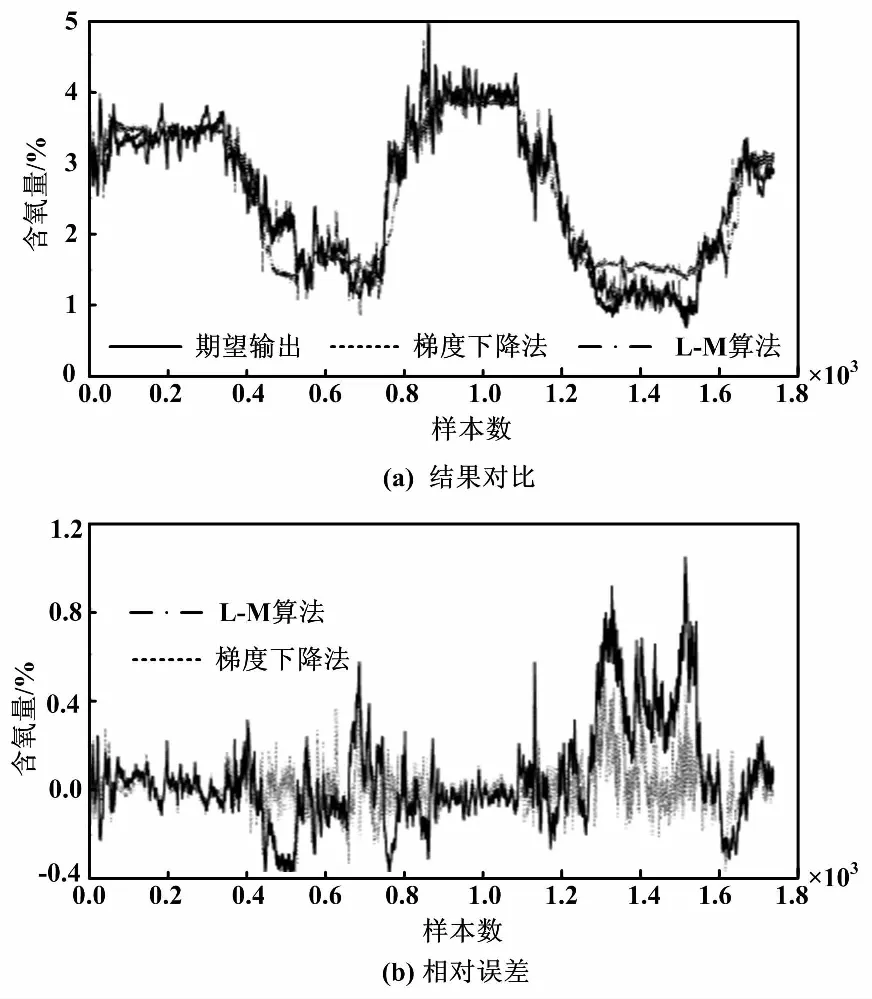
图4 测试结果对比与相对误差曲线Fig.5 Comparison and relative error curves of test result
从图4(a)可以看出,基于梯度下降法和L-M算法的BP神经网络模型都可以预测烟气出口含氧量,其预测值都能够较好地反映真实值的变化。图4(b)表明,两个模型的相对误差总体上都在零轴附近波动,而基于L-M算法训练得到的模型优于梯度下降法。
为了进一步验证模型的预测效果,从其他未经训练的运行数据中以5 s为周期抽取17 280组数据,对模型的预测性能进行测试。含氧测试输出与实际值曲线如图5所示。

图5 含氧测试输出与实际值曲线Fig.5 Test output and actual value curves
为分析两个模型的精度,采用绝对误差(absolute error,AE)和相对误差(relative error,RE)的最大值以及均方误差(mean square error,MSE)等三个评价指标对上述两个模型进行比较。不同训练算法神经网络模型精度对比如表3所示。

表3 不同训练算法神经网络模型精度对比Tab.3 Accuracy comparison of neural network models trained with different algorithm
表3表明,与梯度下降法相比,基于L-M算法的BP神经网络模型预测值更接近尾部烟气出口含氧量平均值,具有更高的预测精度。
5 结束语
近年来,软测量技术作为一种新型的过程变量检测技术,发展迅速且已经得到应用。它解决了传统测量方式的诸多问题,是一种实现在线测量变量的十分有效的检测方式。本文以火电厂风烟系统为研究对象,以某1 000 MW机组为对象,采用神经网络构建尾部烟气出口含氧量软测量模型,并应用火电厂真实历史数据对模型进行训练和验证,比较了基于梯度下降法和L-M算法的BP神经网络模型精度。验证结果表明,与梯度下降法相比,L-M算法网络模型可以更好地预测烟气含氧量,具有更高的预测精度。基于神经网络的烟气出口含氧量软测量为火电厂提供了一种较精确的氧量测量方式,便于运行人员得到良好的在线数据,从而进一步对锅炉燃烧系统进行优化。
