板球系统遗传神经网络PID控制器参数优化研究

王长正，向凤红，毛剑琳

(昆明理工大学信息工程与自动化学院，云南 昆明 650500)

0 引言

板球系统是一个典型的两输入两输出系统，其作为控制领域验证各种控制算法的基本对象，引起了很多学者的关注[1-5]。文献[6]将滑模控制与自适应模糊控制结合，利用蚁群算法优化系统参数，提高了板球系统的轨迹跟踪精度。文献[7]将自适应补偿、监督和间接模糊自适应3种控制算法相结合，提出了间接模糊自适应控制算法，减少小球误差至零邻域内。文献[8]在球杆系统上证明了粒子群算法对比例、积分 、微分(proportion integration differentiation，PID)参数优化的高效性。

PID控制器结构简单、易于操作，被广泛应用于自动化工业控制中[9]。本文提出径向基函数(radial basis funation,RBF)神经网络和遗传算法，结合PID控制器在GPB2001型板球系统上完成定位控制和轨迹跟踪试验。在震荡度、稳定时间和轨迹完成度等方面与RBF-PID控制算法作对比，以证明所提算法的优越性。

1 板球系统建模

选取固高科技公司研发的GBP2001型板球系统作为本文试验平台。板球系统实物模型如图1所示。表1为板球系统参数。

图1 板球系统实物模型Fig.1 Physical model of ball and plate system

表1 板球系统参数Tab.1 Parameters of ball and plate system

由于板球系统的复杂性，对模型进行简化和线性化，在建模过程中作以下4点假设。

①小球在平板上没有滑动和绕小球垂直中心轴旋转的运动[10]。

②不考虑板的角度和面积的限制。

③小球和平板始终接触。

④忽略小球和平板间所有摩擦。

板球系统动力学模型图2所示。

图2 板球系统动力学模型Fig.2 Kinetic model of ball and plate system

利用牛顿定律或拉格朗日方程对其完成分析，可得板球系统x轴和y轴的动力学方程分别如式(1)和式(2)所示：

(1)

(2)

式(1)、式(2)所建立的非线性模型在实际操作中难以实现。因此，我们需要用线性理论来实现模型的线性化，可得线性方程如式(3)、式(4)所示：

(3)

(4)

2 控制器设计

2.1 控制器结构设计

对PID控制器三个参数，即比例(proportion)、积分 (integration) 、微分(differentiation)，进行整定，可使系统达到稳定的控制效果。由于实际应用中系统的耦合性、非线性时变性，数学模型难以确立，传统的PID控制无法在板球系统中达到理想的控制效果[11]。设计的遗传神经网络PID控制器工作原理如下。

①利用遗传算法完成PID参数的经验积累过程。

②将PID参数送至神经网络训练，以实现PID参数的最优化。

③RBF神经网络对被控对象在线辨识，得到被控对象的灵敏度参数，提高控制器精度。

控制器由三部分组成。

①由单神经元PID控制器在闭环控制内控制被控对象，对Kp、Ki、Kd在线调整。

②遗传算法优化PID初始参数，利用RBF神经网络的逼近能力得到一组优化的PID参数值。

③被控对象由RBF神经网络完成在线辨识，同时RBF神经网络对控制对象持续监测，获得输出对输入的灵敏度信息。

遗传神经网络自适应PID控制系统结构如图3所示。

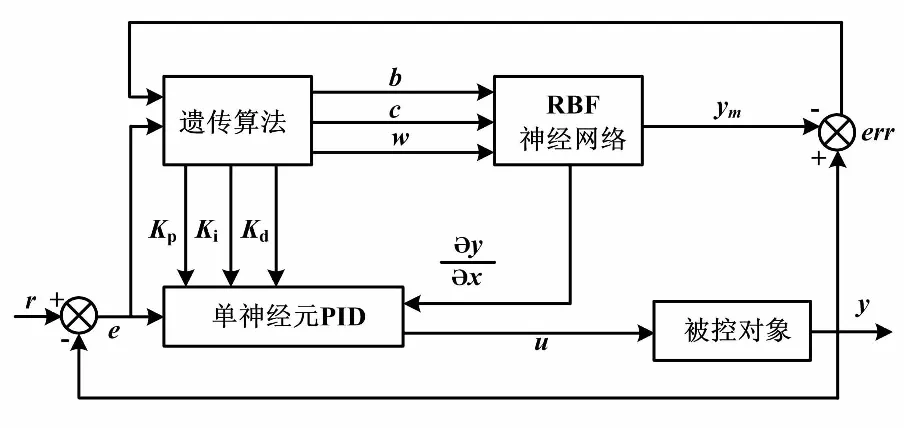
图3 遗传神经网络自适应PID控制系统结构图Fig.3 Structure diagram of genetic neural adaptive PID control system

2.2 单神经元自适应PID

单神经元结合PID，不仅结构简单，而且学习算法速度快。采用数字控制时：

(5)

式中:T为采样周期；u(k)为kT时刻的输入值;e(k)为kT时刻的误差。

单神经元作为构成神经网络的基本单位，是多输入单输出的非线性处理单元。神经元和PID相结合的控制方式，具有自适应性、结构简单、计算量小、权值学习速度快等优点。设：

(6)

(7)

(8)

式(8)与式(5)形式上一致，即神经元与PID结合。f(z)是输入变量x1、x2、x3和权重w1、w2、w3的非线性转移函数，f(z)取为Sigmoid 函数:

(9)

u(k)=Kp(k)f

(10)

在常规PID控制中：

u(k)=Kpz(k)

(11)

Kp、Ki、Kd通过在线学习的方式完成调整。神经网络学习算法选用梯度下降法这一无约束优化算法。梯度下降法沿着梯度负方向前进，权值的调整方向为目标函数梯度变化的反方向，实际输出与期望之间的误差呈减小趋势，即可实现控制的优化目的。

二次型的目标函数为:

(12)

Kp、Ki、Kd的学习算法：

Kx(k+1)=Kx(k)+ΔKx(k)

(13)

(14)

X=P、I、D，η为学习步长，描述如下：

(15)

(16)

(17)

3 遗传算法

3.1 遗传算法描述

遗传算法是一类针对优化问题编码空间的、具有导向的随机化优化搜索方法[12-13]。遗传算法在把握整体局势、优化系统性能方面具有优势，是一种全局搜索能力较强的自适应算法，其收敛性由交叉概率Pc和变异概率Pm的值共同决定。

3.2 基于遗传算法的PID参数优化策略

首先，遗传算法中种群的个体为Kp、Ki和Kd这3个参数，利用适应度函数计算每一组参数的适应度值；然后，在群体中进行选择、交叉和变异操作并不断地进化，直至发现群体中的最优目标，得到PID控制器的最优参数。

基于遗传算法的PID参数初始值优化步骤如下。

①参数用10位二进制编码来表示，确定参数范围，3个参数串接即成为个体，设定种群数量为30，迭代次数为20，交叉概率Pc=0.6，变异概率：

②随机产生初始状态的群体，并计算各个体的适应度值。

③若不需重新生成个体，直接执行步骤④，反之则保留最优个体的同时生成其余个体，并且对重新生成个体的适应度值完成计算，再执行步骤④。

④选择最优个体并存档，在其余个体中选择将要配对的个体。

⑤采用两点交叉和基本变异的方法，对配对完成的个体计算新一代解群中各个体的适应度值。

⑥完成以上步骤后检查解群是否达到终止条件，不满足则重新执行步骤③，满足则跳转至步骤⑦。

⑦最终的Kp、Ki、Kd值送至神经网络学习训练。

4 RBF神经网络

RBF神经网络模拟了人脑中局部调整、相互覆盖接受域的神经网络结构，已证明它能以任意精度逼近任意非线性函数[13]。控制系统的输入量有2个，分别为误差e(k)与误差变化率ec(k)、Kp(k)、Ki(k)、Kd(k)为系统输出量。RBF神经网络中：X=[x1,x2,…,xn]T为输入向量；hj为高斯基函数;H=[h1,h2,…,hm]T为RBF神经网络的径向基向量，即：

(18)

式中:Cj=[cj1,cj2,…,cjm]T为RBF神经网络的第j个节点的中心值向量。

RBF神经网络的宽度向量为：

B=[b1,b2,…,bm]T

(19)

式中：bj为节点j的宽度，bj>0。

W代表权值向量:

W=[w1,w2,…,wm]T

(20)

整个网络输出：

ym(k)=w1h1+w2h2+…+wmhm

(21)

性能指标函数为：

(22)

RBF神经网络可通过训练减小实际与模型期望之间误差，网络的权值学习方法、基宽参数优化算法和中心矢量迭代方法均采用梯度下降法，如式(23)～式(28)：

(23)

ω(k)=ω(k-1)+ω(k)+α[ω(k-1)-ω(k-2)]

(24)

(25)

bj(k)=bj(k-1)+ηΔbj+α[bj(k-1)+bj(k-2)]

(26)

(27)

cij(k)=cij(k-1)+ηΔbij+α[cij(k-1)+cij(k-2)]

(28)

式中:η为学习速率；η∈[0,1]；α为动量因子；α∈[0,1]。

(29)

式中：x1=u(k)。

Jacobian矩阵用来描述被控对象输出量和输入量之间的变化关系，RBF神经网络通过辨识Jacobian矩阵获取所需值。

5 板球系统试验

本文试验基于深圳固高科技公司研发的GBP2001型板球试验平台，按照图3所示的结构搭建控制系统，RBF神经网络的隐含层节点为数目为6。设定以上参数，利用本文设计的PID控制器对GBP2001型板球系统进行仿真试验。遗传算法优化PID参数迭代曲线如图4所示，系统阶跃响应变化曲线如图5所示。

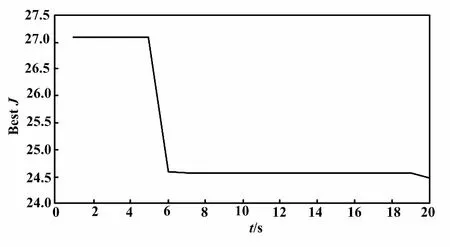
图4 遗传算法优化PID参数迭代曲线Fig.4 Iteration curve of PID parameter optimized by genetic algorithm

图5 系统阶跃响应变化曲线Fig.5 System step response curve

以定位小球于板的中心(0,0)为控制目标，RBF-PID控制输出误差和小球运动轨迹分别如图6和图7所示。可以看出小球在运动控制中已经触碰板的边缘且震荡误差较大，运动轨迹较为复杂，小球经过10 s运动后稳定于板的中心位置。

图6 RBF-PID控制器输出误差图Fig.6 RBF-PID controller output error

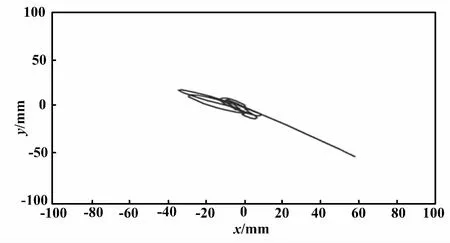
图7 RBF-PID控制小球运动轨迹Fig.7 Ball’s trajectory of RBF-PID control

设计GA_RBF-PID控制器，选择控制较优的试验并导出小球运行数据，在MATLAB中完成图形绘制。GA_RBF-PID控制器输出误差如图8所示。GA_RBF-PID控制为小球运动轨迹如图9所示。由图8和图9可知，小球在板上的位移偏差减小很多，小球整体的运动轨迹与RBF-PID控制的运动轨迹相比更加简洁，小球达到稳定状态(球板中心)的时间也缩短至约6.5 s。以上试验证明，GA_RBF-PID控制在板球系统定位试验中的控制效果优于RBF-PID控制。

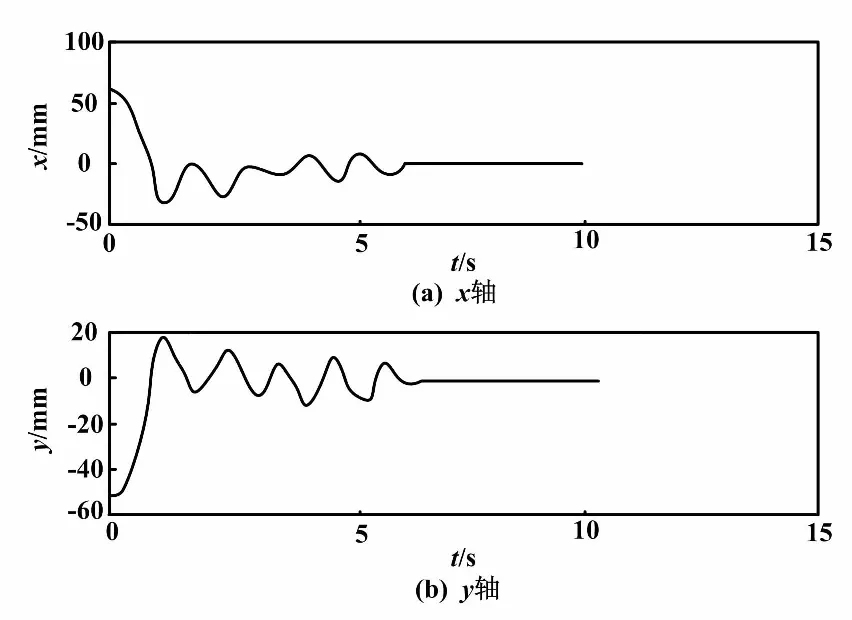
图8 GA_RBF-PID控制器输出误差图Fig.8 GA_RBF-PID controller output error

图9 GA_RBF-PID控制小球运动轨迹Fig.9 Ball’s trajectory of GA_RBF-PID control

RBF-PID控制结果与GA_RBF-PID控制结果具体数据对比见表2。从表2可以看出，GA_RBF-PID控制在精确度和时效性上都有一定的提高，并且使小球的稳定位置更接近于控制位置，有效减小了位置控制试验中的误差。

表2 控制结果对比Tab.2 Comparison of control results

采用RBF-PID和GA_RBF-PID控制完成GBP2001板球系统的轨迹跟踪控制试验。小球方形轨迹跟踪如图10所示。

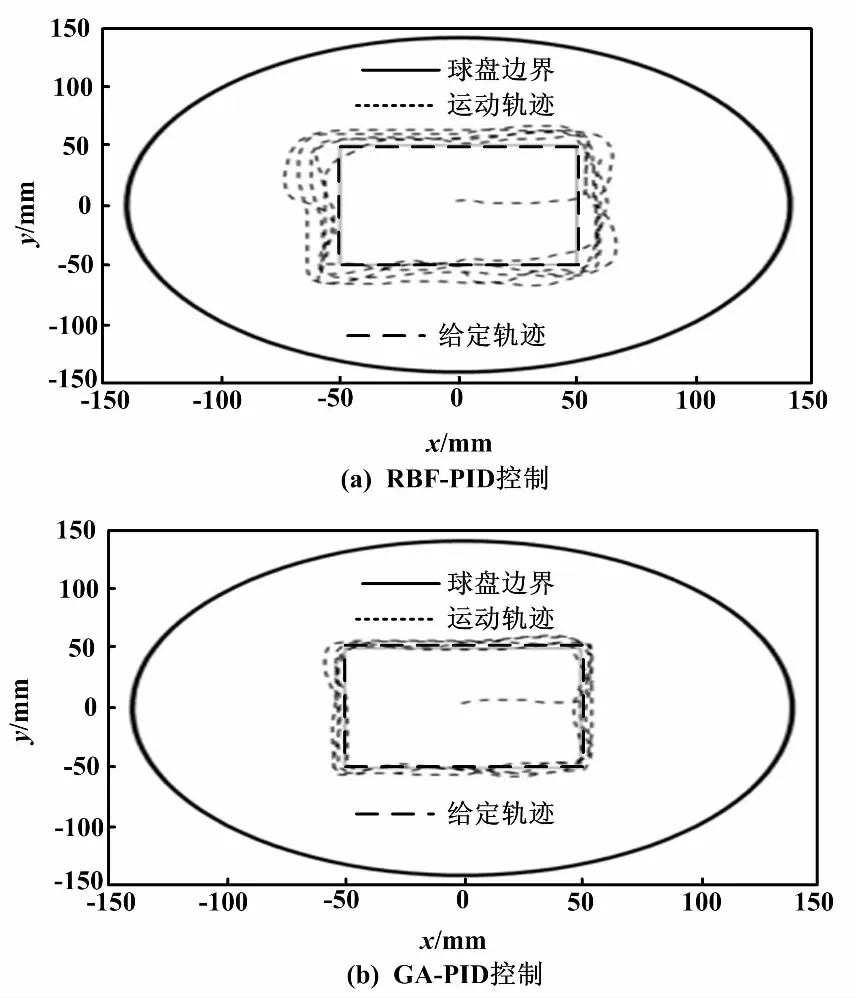
图10 小球方形轨迹跟踪Fig.10 Square trajectory tracking of ball

由图10可知，小球在球盘上运动过程中，在正方形四个顶点处小球的目标位置和小球的运动方向均要发生变化。由于小球的惯性产生系统响应延迟，在四个顶点位置后的一段轨迹波动较大。在RBF-PID控制过程中，小球的误差较大，运动曲线不够稳定，对于设定的方形轨迹不能精确复现。在GA_RBF-PID控制过程中，随着小球运动时间的增加，误差越来越小，轨迹跟踪精度越来越高，能够完成方形轨迹的精确跟踪。轨迹跟踪控制实际上可看成是连续的位置控制运动。试验结果证明，本文提出的GA_RBF-PID控制算法对板球系统的轨迹跟踪在误差允许的范围内可行、有效。

6 结束语

由于板球系统是一个多变量、不稳定、非线性耦合的开环控制系统，在高等院校、科研院所中应用广泛，定位控制和轨迹跟踪控制对于验证控制算法有效性有着重要意义。本文采用遗传神经自适应PID控制方法对板球系统进行定位控制和轨迹跟踪。试验结果表明，RBF-PID和GA_RBF-PID控制算法均完成了板球系统的定位跟踪和方形轨迹跟踪控制，GA_RBF-PID 控制算法在轨迹跟踪试验中轨迹的相似度较高，控制精度优于RBF-PID控制，加强了板球系统控制的实时性。下一步计划完善板球系统的数学模型，并在视觉检测方面，能够更快更准确地检测小球位置标信息，从而完成板球系统的高精度轨迹跟踪。