井壁失稳风险的可靠度理论评价方法

2019-04-08陈颖杰邓传光马天寿

天然气工业 2019年11期

陈颖杰邓传光马天寿

1. 中国石油西南油气田公司勘探事业部 2. “油气藏地质及开发工程”国家重点实验室·西南石油大学

0 引言

井壁失稳问题是钻井工程中非常棘手的井下复杂或事故，井壁失稳通常表现为井壁坍塌和井眼漏失，准确控制井筒压力高于坍塌压力并低于破裂压力，可以有效避免井壁失稳事故，还可以避免诱发产生的井喷、井漏、井塌、卡钻等井下复杂和事故[1-3]。

国内外学者针对井壁稳定问题已经开展了较为深入的研究，建立多种经验模型、解析模型和数值模拟方法[2-6]。研究的焦点主要集中于本构模型和破坏准则，本构模型方面已经形成了线弹性解析解、塑性模型、弹塑性模型、孔隙弹性模型、孔隙热弹性模型、化学孔隙弹性模型、化学孔隙热弹性模型等多种模型[6-17]，破坏准则方面已经形成了Mohr-Coulomb准则、Drucker-Prager准则、Mogi-Coulomb准则、修正Lade准则、修正Wiebols-Cook准则、Hoek-Brown准则等多种准则[18-20]。但是，由于深部地层地质条件的隐蔽性和不确定性，加之地球物理测井及其解释方法均存在一定误差，使得地层地质力学参数（地应力、孔隙压力）、岩石力学参数等呈现出较强的不确定性，进行井壁稳定分析时将难以确定准确的输入参数。若输入参数出现一定偏差，将导致井壁稳定分析结果出现偏差，甚至可能出现严重错误[4-5]。在国外，一些学者采用定量风险分析方法定量研究了输入参数不确定性特征，并且明确了输入参数不确定程度对井壁稳定分析结果的影响[21-25]；在国内，张立松等推导了煤层气直井坍塌压力可靠度计算公式[26]，魏凯等[27-28]建立了直井井壁失稳区域识别方法，可见国内针对输入参数不确定性及对井壁稳定分析结果影响的研究较少，参数不确定性对井壁稳定分析结果的影响尚不明确。为此，笔者基于可靠性理论，建立井壁稳定风险评价方法，定量评价直井井壁失稳的风险，并进行参数不确定性的影响分析与评价，以期为直井井壁稳定控制和措施的制定提供理论支撑。

1 井壁稳定力学模型

1.1 井壁应力分布

对于直井而言，在井眼圆柱坐标系(r，θ，z)中，井壁处的应力可取Kirsch方程中r=rw并整理得到[1-2]：

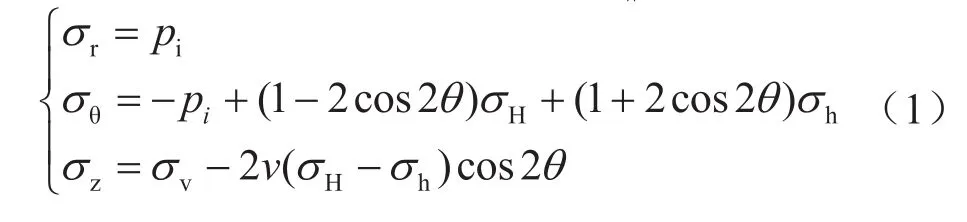
式中σr，σθ，σz分别表示井周径向、环向和轴向应力，MPa；σH，σh，σv分别表示最大、最小水平地应力和上覆岩层压力，MPa；pi表示井筒液柱压力，MPa；v表示泊松比；θ表示井壁任意位置对应的圆周角，( °)。

1.2 坍塌压力计算模型

强度准则的选取是井壁坍塌压力计算另一个非常重要的方面，最常用的强度准则是Mohr-Coulomb准则、Drucker-Prager准则、Hoek-Brown准则等。实践表明，对于比较坚硬的岩石，Mohr-Coulomb准则计算结果比较可靠，此处采用Mohr-Coulomb准则，即：

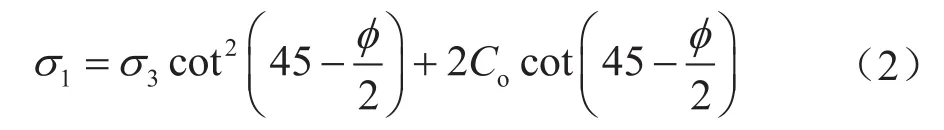
式中σ1，σ3分别表示最大、最小地应力，MPa；Co表示内聚力，MPa；表示内摩擦角，( °)。

岩石剪切破坏与否主要取决于所受的应力状态，最大、最小主应力差值越大，则井壁坍塌越容易发生。通常情况下，井壁处最大、最小主应力分别为环向应力和径向应力，即井壁是否坍塌主要取决于于井壁环向应力（σθ）和径向应力（σr）的差值。由式（1）不难看出：当井周角θ=±π/2时，环向应力达到最大值，而该处的差应力（σθ-σr）将达到最大值，说明井壁坍塌失稳的临界点位于θ=±π/2处，即井壁失稳的方位与最小水平地应力方向一致。若考虑岩石非线性特性和岩石孔隙中所作用的孔隙压力（pp），则井壁失稳临界点的最大和最小有效应力[2]：

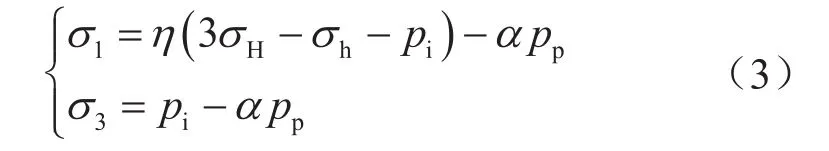
式中α表示Biot系数；pp表示地层孔隙压力，MPa；pi表示钻井液柱压力，MPa；η表示应力非线性修正系数，一般η=0.95。

于是，将式（3）带入式（2）得坍塌压力计算模型[2]：

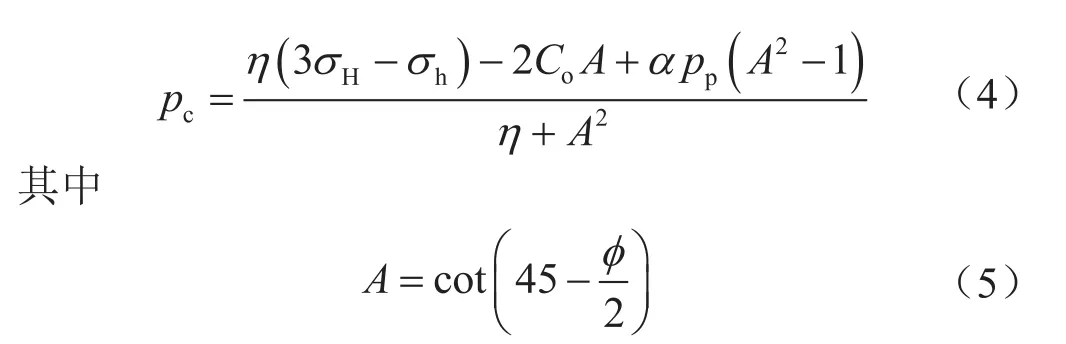
式中pc表示坍塌压力，MPa。

1.3 破裂压力计算模型

当井内的钻井液柱所产生的压力高到足以压裂地层，使其原有的裂隙张开延伸或形成新的裂隙时的井内流体压力称为地层的破裂压力（pf）。地层破裂是由于井内钻井液密度过大使岩石所受的周向应力达到岩石的抗拉强度而造成的，即

式中St表示岩石抗拉强度，MPa。

由式（1）不难看出：当井筒压力增大时，环向应力变小；当井筒压力增大到一定程度时，环向应力将变成负值，即岩石所受周向应力由压缩应力变为拉伸应力，当拉伸应力大到足以克服岩石的抗拉强度时，地层则产生破裂造成井漏。破裂发生在环向应力最小处，即井壁破裂的临界点位于θ= 0°或π处。若考虑岩石孔隙中所作用的pp，则井壁破裂临界点的最小有效应力为：

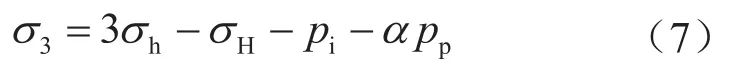
于是，将式（7）带入式（6）可得压裂井壁的临界压力值，即破裂压力[2]：

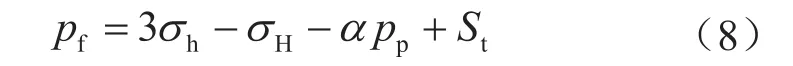
式中pf表示破裂压力，MPa。

2 井壁失稳风险可靠度评价方法构建

根据可靠性理论，假设井壁稳定的功能函数具有如下的一般形式：

将功能函数（Z）在均值点(称为中心点)处展开成Taylor级数并保留至一次项，即

根据相互独立正态分布随机变量线性组合的性质，则Z的均值和方差可分别表示如下[29]：

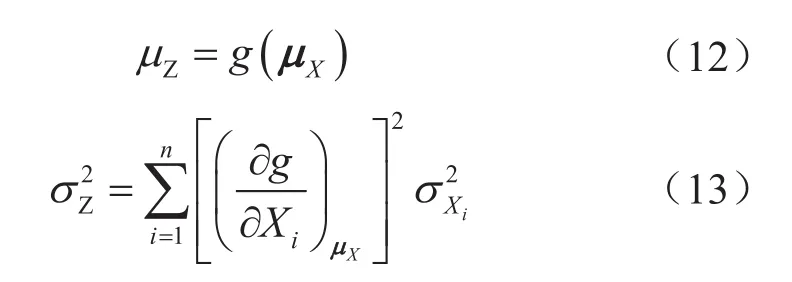
式中μZ表示功能函数Z的均值；σZ表示功能函数Z的方差。

根据可靠度指标的定义，由式(13)、(14)可得可靠度指标[29]：

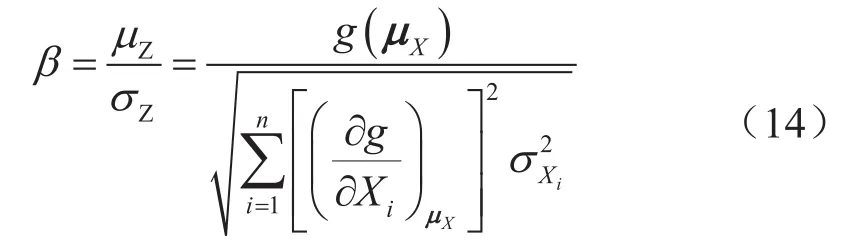
式中β表示可靠度指标。

上述方法将功能函数Z在随机变量的均值点展开成Taylor级数并取一次项，利用X的一阶矩（均值）和二阶矩（方差）计算Z的可靠度，所以又称为均值一次二阶矩方法[29]。当已知X的均值和方差时，可用此方法简便地估算可靠度指标。通常情况下，将功能函数处于失稳状态下的概率称为失稳概率，若功能函数符合正态分布，则井壁失稳的概率和井壁稳定的可靠度概率可表示[29]：

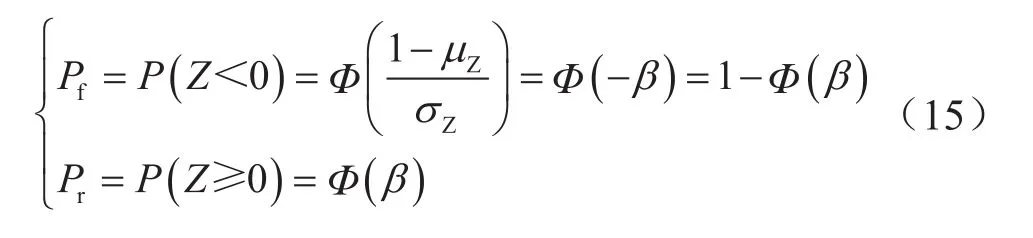
式中Pf表示井壁失稳的概率；Pr表示井壁稳定的概率；Φ表示标准正态分布函数。

因此，将式（10）带入式（12）～（13），计算井壁坍塌和破裂两种情况下功能函数（Z）的均值（μZ）和方差（σZ）；进一步，将功能函数（Z）的均值（μZ）和方差（σZ）带入式(14)，计算可靠度指标（β）；最后，将可靠度指标（β）带入式（15），可计算出井壁失稳和井壁稳定所对应的概率，此二者之和为1，从而可实现井壁失稳风险的定量评价。

3 应用分析

3.1 基础输入参数不确定性分析

井壁坍塌压力和破裂压力的计算主要涉及如下输入参数：井筒压力、最大水平地应力、最小水平地应力、孔隙压力、岩石强度（内聚力、内摩擦角和抗张强度）、应力非线性修正系数、Biot系数等，其中，井筒压力、应力非线性修正系数和Biot系数基本可以认为是确定输入参数，而最大水平地应力、最小水平地应力、孔隙压力、岩石强度(内聚力、内摩擦角和抗张强度)具有一定的不确定性。描述参数不确定性的数学方法主要有均匀分布、三角分布、正态分布、Beta分布、Weibull分布、Gamma分布等多种，通常这些参数基本上能够满足正态分布。

为了分析输入参数不确定性特征，以四川盆地X井为例进行分析，该井须家河组埋深介于4 200～4 500 m，测井和实钻资料表明，该井所在地区的上覆岩层压力梯度介于2.27～3.02 MPa/100 m、水平最大地应力梯度介于1.85～2.59 MPa/100 m、水平最小地应力梯度介于1.55～2.16 MPa/100 m、地层孔隙压力梯度介于1.17～1.45 MPa/100 m、地层岩石内聚力介于14.25～22.25 MPa，岩石内摩擦角介于31.25°～35.46°，岩石抗张强度介于4.65～7.48 MPa。根据测井解释结果给定各参数的均值，参考现场各种测试方法计算相关参数可能的误差范围[14]设定各参数的标准差和变异系数（标准差与均值的比值），给定各参数的不确定性统计结果如表1所示，通过蒙特卡洛模拟得到的地应力、岩石强度等参数分布拟合结果如图1所示。不难看出，各参数的不确定分布规律满足正态分布规律；变异系数越高，则样本数据的不确定性越强，参数的分布越广泛，对井壁稳定分析结果的影响将更加显著；反之亦然。可见这种强烈的参数不确定性势必会对井壁稳定性分析结果产生显著影响。

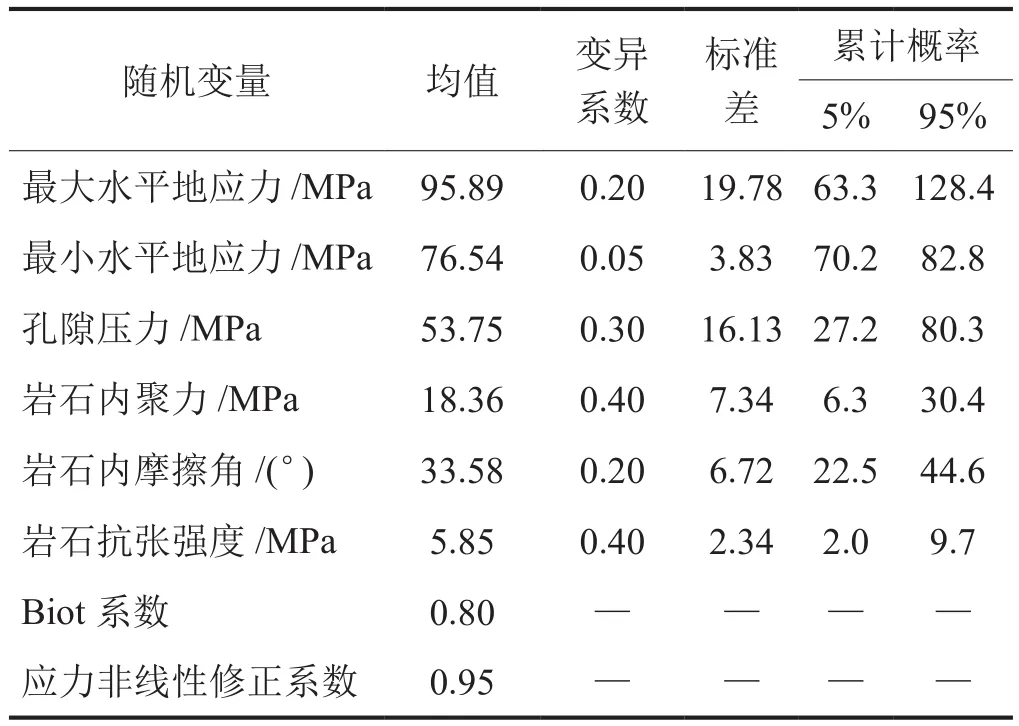
表1 输入参数不确定性特征统计表

3.2 不同钻井液当量密度下可靠度评价结果

为了计算不同井筒压力下井壁稳定的可靠度概率，取不同井筒钻井液当量密度值，按第2节所述的方法计算了不同钻井液当量密度下防止井壁坍塌和井壁破裂的可靠概率，如图2所示。

由图2可知，随着井筒钻井液当量密度的增加，井壁坍塌条件所对应的可靠概率逐渐增加，而井壁破裂条件所对应的可靠概率逐渐降低。这充分说明，随着井筒钻井液当量密度的增加，一方面井壁坍塌的风险逐渐降低，因而井壁保持稳定的概率逐渐增加；另一方面井壁破裂的风险又逐渐增加，使得井壁被压漏的概率逐渐增加。因此，需要寻找一个合适的井筒钻井液当量密度，使得防止井壁坍塌和漏失的可靠概率均保持在较高的概率。通常情况下，井壁坍塌和井壁破裂可靠概率曲线都会存在一个交点，该交点的意思是井壁坍塌和井壁破裂为等概率事件，在低于该交点对应的概率情况下将能够找到一个合适的安全窗口、而高于该交点将不存在安全窗口。图2中标出了3种典型的情况，这3种情况可以分为两类，第一类是要求比较高的可靠概率(90%)，由于井壁坍塌和井壁破裂可靠概率曲线的交点出现在当量密度为1.65 g/cm3，而此时对应的坍塌压力和破裂压力当量密度分别为1.78 g/cm3和1.45 g/cm3，这二者之间并没有安全窗口，说明此时难以在该类地层中实现这一目标；第二类为了能够在较为安全的概率下成功钻穿该地层，可以适当的选择恰当的可靠概率，比如将可靠概率定为80%或70%，这两种情况对应的安全窗口分别介于1.58～1.73 g/cm3和1.45～1.92 g/cm3，可靠概率80%对应的安全窗口明显小于可靠概率70%的情形，这说明适当地选择工程上可以接受的概率范围，可以在更宽的安全窗口内设计井筒钻井液密度。但是，工程上通常需要将可靠概率控制在80%以上，这样钻穿该地层的成功率将会达到比较理想的效果。

3.3 输入参数不确定程度的影响

3.3.1 地应力的影响

地应力不确定性对井壁稳定分析结果的影响可以分为两个主要的方面，一方面是最大水平地应力的影响，另一方面是最小水平地应力的影响。为了明确这两方面因素的影响规律，计算了最大和最小水平地应力在变异系数分别为0、0.1、0.2、0.3、0.4这5种情况下不同当量密度所对应的井壁稳定可靠度概率，结果如图3所示。

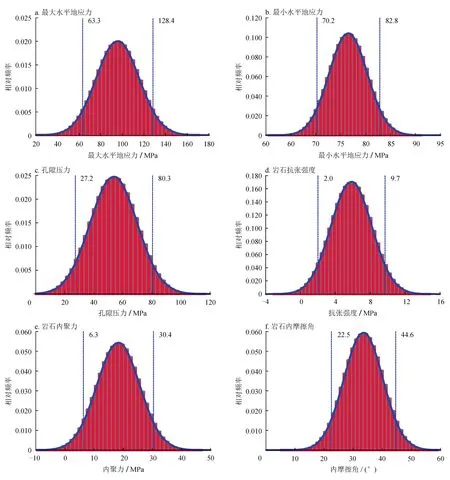
图1 基本输入参数正态分布特征图

由图3可知，①随着水平地应力变异系数的增加，井壁坍塌和井壁破裂可靠概率曲线的交点下降，②图3-a显示出现的位置基本上在当量密度为1.65 g/cm3，5种情况下交点对应的可靠概率下降，分别为93.3%、90.2%、83.5%、78.0%和73.5%；③图3-b显示交点出现的位置随变异系数的增加而逐渐向左移动，且5种情况下交点对应的可靠概率也逐渐降低，分别为 85.7%、80.5%、73.4%、68.5% 和 64.8%；④图3-b还显示井壁坍塌可靠概率曲线受到的最小水平地应力变异系数影响较小。综上所述，地应力不确定性对井壁稳定影响显著，其中，最大水平地应力不确定程度对井壁坍塌和井壁破裂均有显著影响，而最小水平地应力不确定程度主要影响井壁破裂。井壁稳定分析中需要准确确定地应力的大小，不确定程度越低，则井壁稳定分析结果的可信度越高，所确定的井壁稳定安全窗口也将更加准确。

3.3.2 孔隙压力的影响

地层孔隙压力对井壁稳定分析结果也具有显著的影响，为了明确这方面因素的影响规律，计算了孔隙压力在变异系数分别为0、0.1、0.2、0.3、0.4这5种情况下不同当量密度所对应的井壁稳定可靠度概率，结果如图4所示。

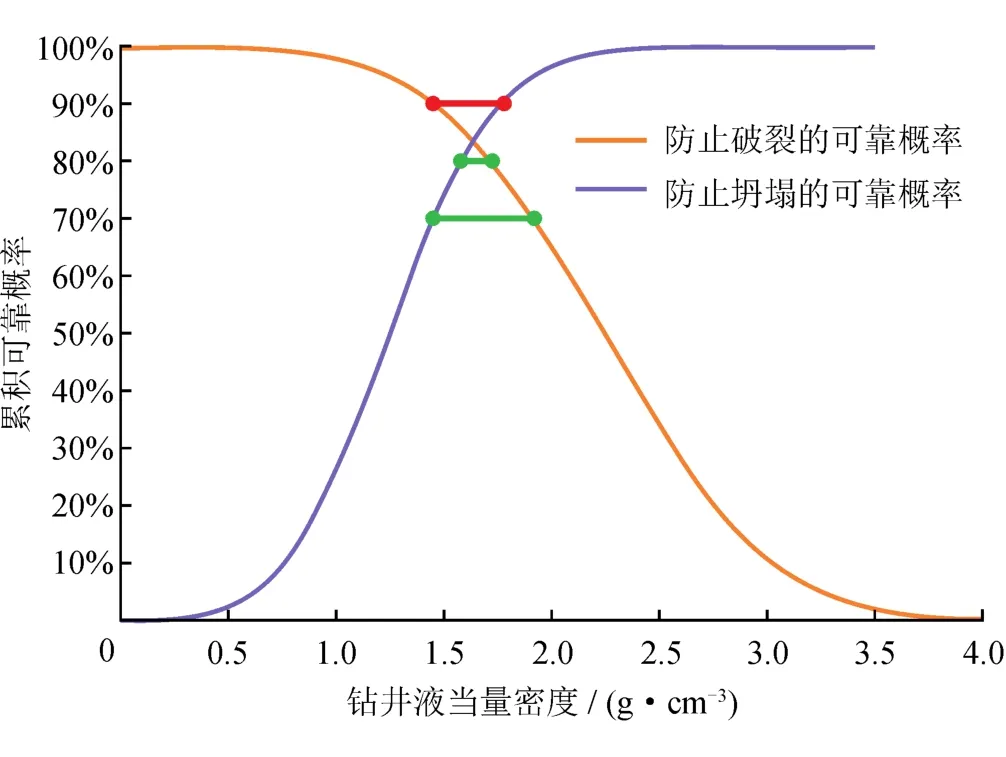
图2 不同当量密度下的井壁稳定可靠度概率图

由图4可知，随着孔隙压力变异系数的增加，井壁坍塌和井壁破裂可靠概率曲线的交点出现的位置出现在1.64～1.66 g/cm3，但这5种情况下交点对应的可靠概率略微降低，分别为87.5%、86.6%、85.7%、83.5%和82.5%，井壁坍塌和井壁破裂可靠概率曲线反映出对井壁稳定安全窗口不如地应力的影响显著，但对于一些窄安全密度窗口地层，其影响将不容忽视。

3.3.3 岩石强度的影响

地层岩石强度对井壁稳定分析结果也具有一定的影响，为了明确这方面因素的影响规律，计算了岩石内聚力、内摩擦角和抗张强度在变异系数分别为0、0.1、0.2、0.3、0.4这5种情况下不同当量密度所对应的井壁稳定可靠度概率，岩石强度参数不确定程度对井壁稳定分析结果的影响如图5所示。

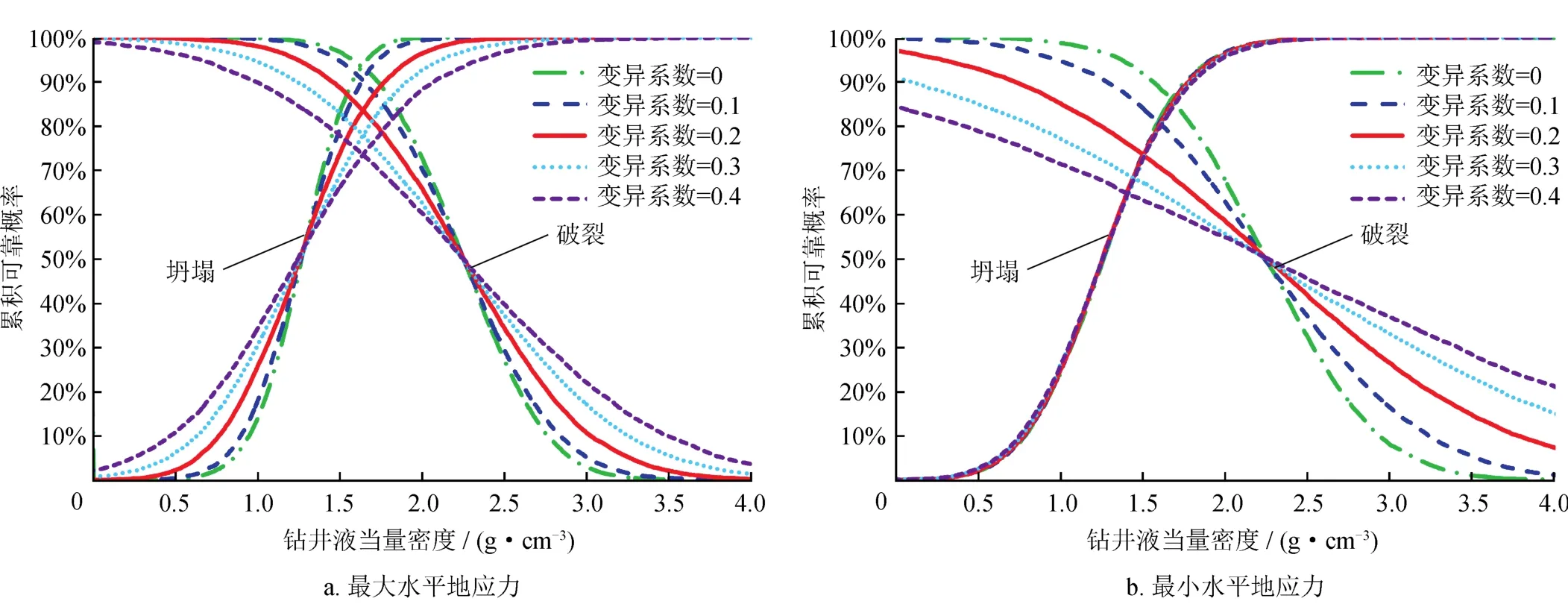
图3 最大、最小水平地应力不确定程度对井壁稳定分析结果的影响图

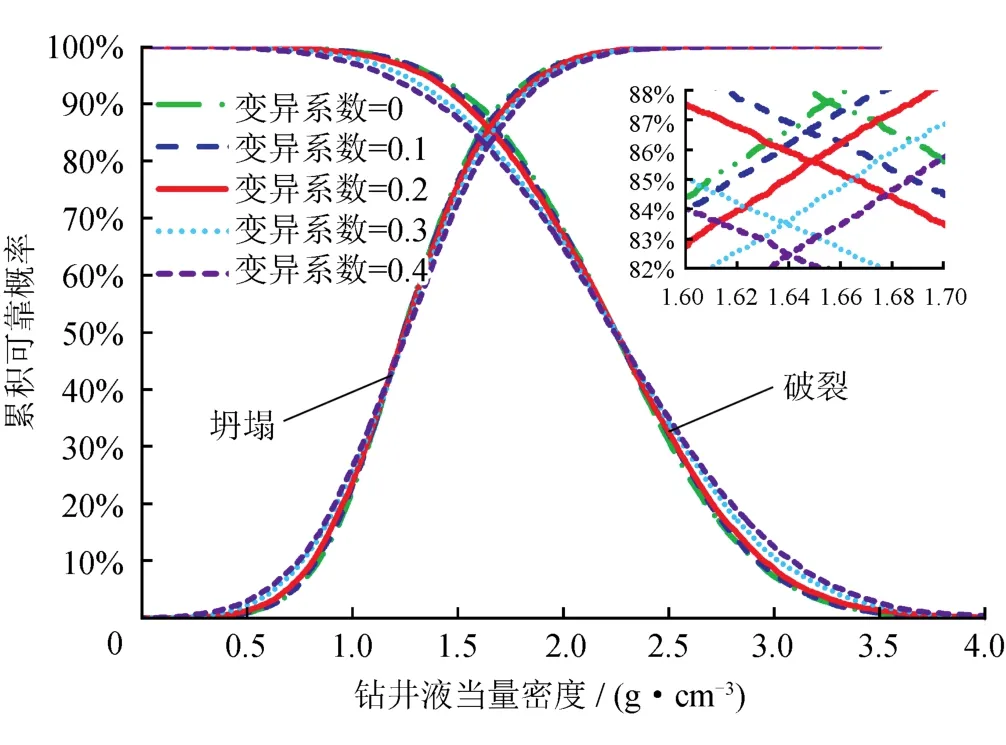
图4 孔隙压力不确定程度对井壁稳定分析结果的影响图

1）对于岩石内聚力和内摩擦角而言，①随着内聚力和内摩擦角变异系数的增加，井壁坍塌可靠概率曲线受到了一定程度的影响，其受影响程度与地应力相比较小，但井壁破裂可靠概率曲线并未受到影响；②在岩石内聚力变异系数由0增加至0.4的过程中，井壁坍塌和井壁破裂可靠概率曲线的交点出现的位置随变异系数的增加而逐渐向右移动，但基本上都在当量密度为1.62～1.65 g/cm3的范围内，而且这5种情况下交点对应的可靠概率也略微降低，分别为84.8%、84.7%、84.6%、84.5%和83.9%；③在岩石内摩擦角变异系数由0增加至0.4的过程中，井壁坍塌和井壁破裂可靠概率曲线的交点出现的位置也随变异系数的增加而逐渐向右移动，但基本上都在当量密度为1.62～1.68 g/cm3的范围内，而且这5种情况下交点对应的可靠概率也略微降低，分别为84.6%、84.6%、83.8%、83.5%和82.7%。

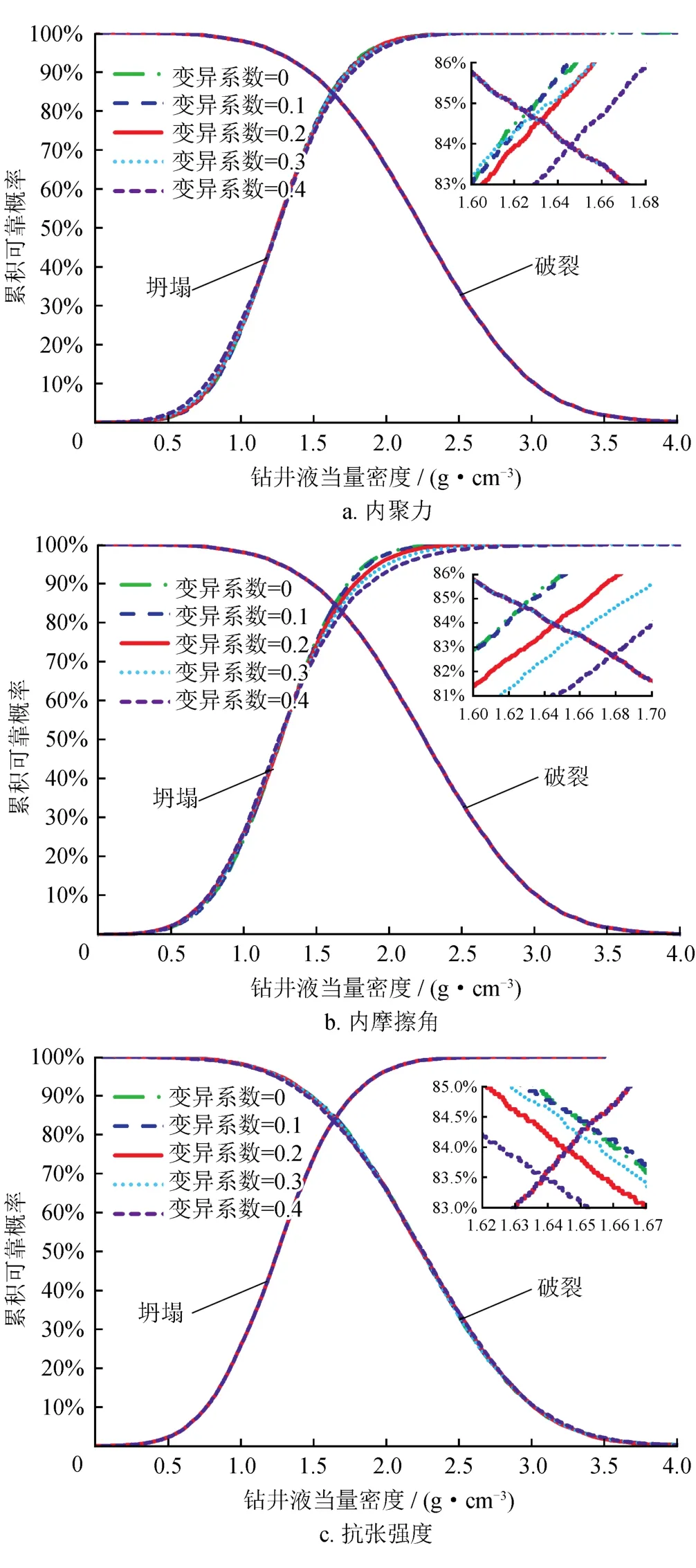
图5 岩石强度参数不确定程度对井壁稳定分析结果的影响图

2）对于岩石抗张强度而言，①随着抗张强度变异系数的增加，井壁破裂可靠概率曲线受到了一定程度的影响，其受影响程度与地应力相比较小，但井壁坍塌可靠概率曲线并未受到影响；②在岩石抗张强度变异系数由0增加至0.4的过程中，井壁坍塌和井壁破裂可靠概率曲线的交点出现的位置随变异系数的增加而逐渐向左移动，但基本上都在当量密度为1.63～1.66 g/cm3的范围内，而且这5种情况下交点对应的可靠概率也略微降低，分别为84.3%、84.3%、84.2%、84.0%和83.5%。因此，岩石强度的不确定性对井壁稳定的安全窗口分析结果具有一定影响，尽管对井壁稳定安全窗口分析结果影响并不显著，但对于一些窄安全密度窗口地层，其影响将不容忽视。