双相钢DP780在高应变速率下的力学本构表征研究

项正波，方 刚

（1.麦格纳卫蓝新能源汽车技术（镇江）有限公司 上海分公司，上海 201821；2.中国汽车工程研究院，重庆 401122）

随着汽车轻量化与安全法规的要求日趋严格，尤其对于新能源汽车，高强度钢在车身结构上的应用也越来越广泛。计算机辅助工程（Computer Aided Engineering，CAE）技术作为一种在汽车安全性能开发过程中的重要方法，相比传统的碰撞试验，具有缩短研发周期、节约开发成本、提高工作效率等优势。

准确的CAE分析离不开精确的材料力学行为表征，即材料在高应变速率下应力-应变行为的数学描述[1]。金属材料在拉伸试验中主要经历3个阶段，即弹性阶段、塑性阶段和损伤阶段（表现为缩颈断裂），其中，弹性阶段和塑性阶段的转折点为塑性起始点，一般用塑性准则进行表征。材料的本构关系是在大量的试验基础上，采用数学-物理模型建立材料本构方程。通常材料在静态和动态条件下的力学行为表现差异很大，最直观的表现为材料应变速率敏感性[2]。材料的应力与应变、温度、应变率都密切相关，其力学行为一般用热粘塑性本构模型来描述。在较早的研究中，相关学者已经提出了一些用于描述多晶材料高应变速率下塑性变形的本构模型，常用的模型有：

Johnson-Cook（JC）模型[3]。

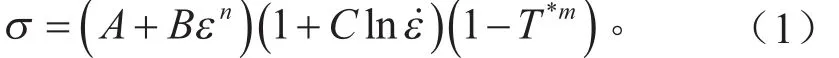
式中：σ为Mises流动应力；ε˙)为等效塑性应变；˙)为无量纲塑性应变率；A，B，C，n和m为材料常数；T* = (T−Tr) /(Tm−Tr)，T为试验温度，Tr为室温，Tm为材料的熔点。

Cowper-symonds（Cs）模型[4]。

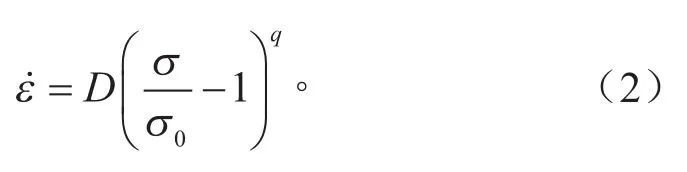
式中：σ0为准静态应力；D，q为常数。

针对体心立方体（Body-centered Cubic structure，BCC）金属的Zerilli-Armstrong（ZA）模型[5]。

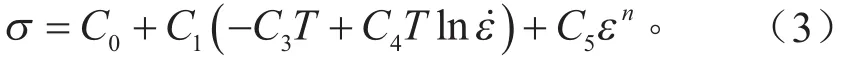
式中：C0，C1，C2，C3，C4，C5和n为常数；T为绝对温度。

JC模型和Cs模型是基于加工硬化和应变敏感性的数学表达，它们在数学上表达形式是乘积的关系。如图1a所示，不同应变速率时计算得出的应力-应变关系表现为发散形式。ZA模型的数学表达为累加关系，在不同应变速率条件下的应力-应变关系表现为平行形式，如图1b所示。

YAN等[6]在研究中发现，一些高应变速率试验结果是发散的。而CADY等[7]在研究某些汽车高强度钢的高速应变行为时发现，高应变时流变应力达到饱和，如图1c所示的收敛的应力-应变曲线。研究DQsK钢在室温下3种应变速率的力学特征时，其试验数据与JC模型计算结果存在巨大差异，特别是在准静态或低应变速率条件下，如图2所示。因此，由JC模型、Cs模型和ZA模型预测的应力-应变关系，不能完全包含各类材料在高速应变速率下所有的真实数据状态。

为了表示图1中可能出现的3种状况，需要扩充新的材料本构模型。新的本构模型基于传统JC模型，称为“修正JC模型”。

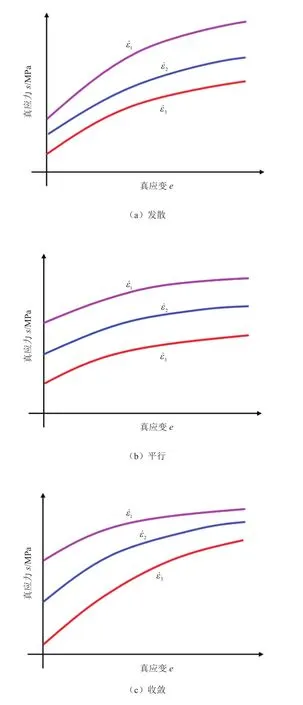
图1 各种形式的应力-应变曲线（＞ ˙＞ ）

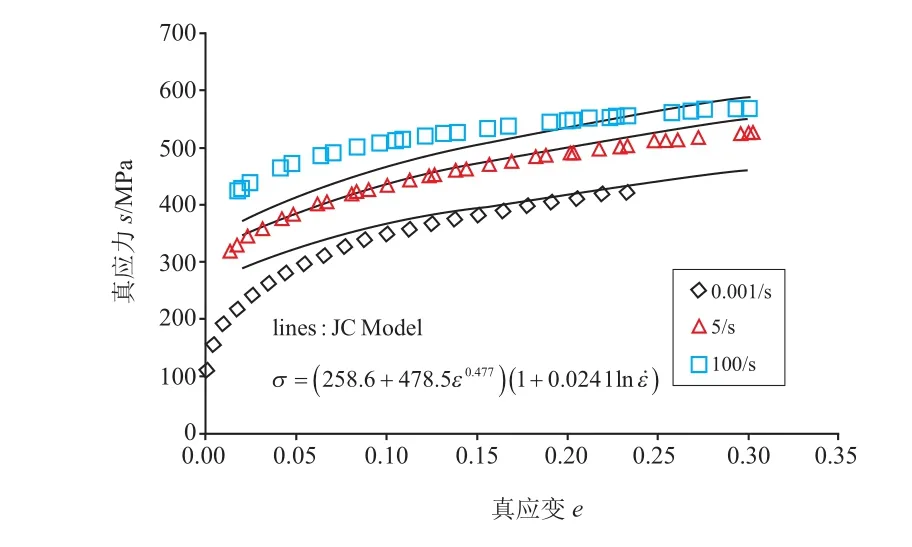
图2 JC模型结果和试验数据的巨大差异[6,8]

1 修正JC模型

材料动态力学性能数据在整车安全CAE分析中，通常只关注材料在室温条件下的结果。因此，修正JC模型不考虑材料对温度的依赖性，其数学表达式如下。

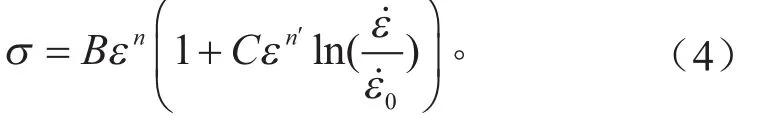
式中：B，C，n和n'为材料常数。当时，B和n通过静态应力-应变数据拟合得到。

修正JC模型与传统JC模型的差异讨论如下。

（2）修正JC模型中，指数εn使模型适用于不同的应力-应变行为形式：当n+n'＞0，模型可以描述发散；当n+n'=0，模型可以描述平行；当n+n'＜0，模型可以描述收敛。

2 动态力学性能试验

2.1 试验材料

本试验的试验材料为DP780，材料厚度为1.6 mm，取样方向为沿轧制方向，样品尺寸如图3所示。

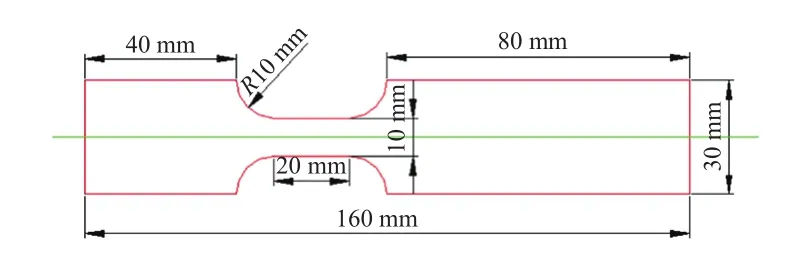
图3 材料动态力学性能试验样品尺寸

2.2 试验设备

试验在中国汽车工程研究院ZWICK HTM 5020高速拉伸试验机上进行，应变测量采用全应变场光学测量系统，如图4所示。试验过程中，应变速率在0.001/s、1/s、100/s条件下，载荷使用设备自带载荷传感器进行采集；应变速率在500/s条件下，载荷使用（在试验样品加持部分弹性变形区域贴应变片）应变片进行采集；在所有应变速率条件下的变形均采用全场应变采集系统进行采集，并采用VIC-2D软件进行应变分析。

图4 材料高速拉伸试验机及全应变场光学测量系统

2.3 试验条件

试 验 参 照 IsO 26203—2、sEP1230、T/CsAE 52—2016执行，分别在应变速率为0.001/s、1/s、100/s、500/s条件下进行材料力学性能试验。数据处理过程中，各参量物理意义及计算方法如下。

（1）真实应变：εT=ln(1 +ε)，ε为工程应变。

（2）真实应力：σT=σ× (1 +ε)，σ、ε分别为工程应力应变。

（3）真塑性应变：εplastic=εT−σT/E，E为弹性模量。

试验结果如图5所示。

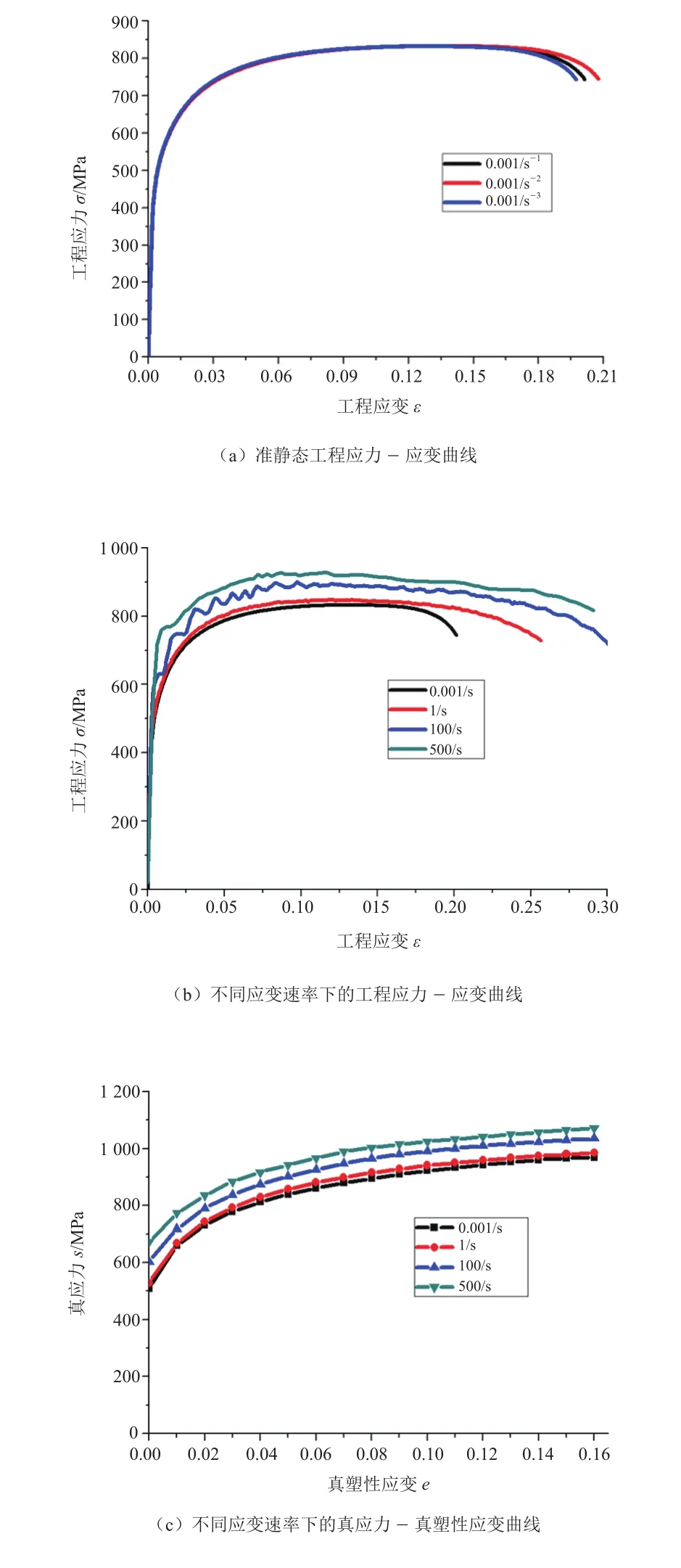
图5 材料力学性能试验结果

3 数据分析与讨论

为了更好地获得双相钢在不同应变速率条件下的本构表征，分别采用传统JC模型和修正JC模型对试验结果进行拟合，拟合结果如图6～7所示。

由图6～7可知，对于相同的双相钢DP780试验数据，修正JC模型能更好地表征不同应变速率条件下材料的力学行为。修正JC模型中各参数拟合值分别为：B=1 299.43，C=0.004 8，n=0.15，n'=-0.18，由于n+n'＜0，所以对双相钢DP780而言，修正JC模型对试验数据有更好的表征（能够有效地反映曲线的收敛）。

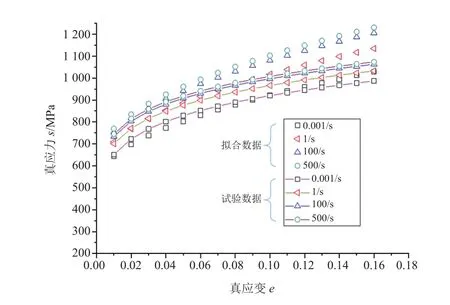
图6 基于传统JC模型的数据处理曲线

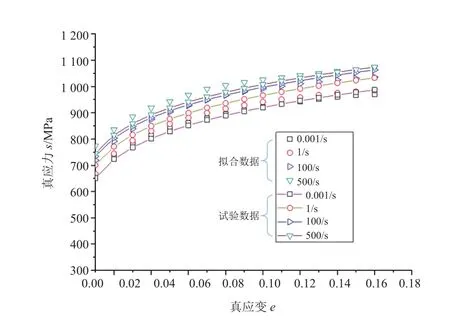
图7 基于修正JC模型的数据处理曲线

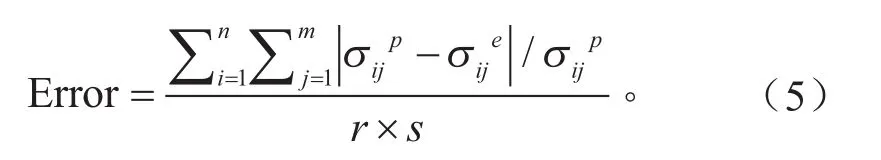
利用预测值与1%应变间隔计算所得试验数据差值的百分数，对拟合质量进行评估，误差计算方法如下。和分别为试验和拟合得到的等效应力；s为动态应力-应变曲线的数量；r为每条动态应力-应变曲线上的数据点数。

图6～7中，传统JC模型平均误差为6.43%，修正JC模型平均误差为2.21%；修正JC模型的平均误差率比传统JC模型缩小4.22%，其精度提高了65.7%。修正JC模型和传统JC模型在收敛应力-应变曲线下的对比，如图8所示。

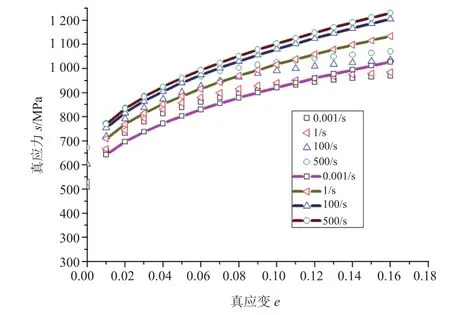
图8 修正JC模型和传统JC模型在收敛应力-应变曲线下的对比曲线

4 结论

（1）本文对双相钢DP780在高应变速率下的试验数据进行研究，试验获得的双相钢DP780在高应变速率下的应力-应变曲线表现为收敛关系，且采用修正JC模型能准确地进行表征。

（2）通过修正JC模型得到的双相钢DP780在高应变速率下的应力-应变数据，与传统JC模型相比，其精度提升约65%。

本文仅针对双相钢DP780的动态力学行为进行了修正JC模型和传统JC模型的比对分析，双相钢通常为两相组织，修正JC模型能否有效表征软钢、单一马氏体钢在动态条件下的力学行为仍需进一步研究[9]。同时，相比传统JC模型，修正JC模型不能够表征材料的屈服强度，其完善工作仍需进一步研究和探讨。