土壤侵蚀临界切应力的计算研究评述

(汕头大学环境与土木工程系 广东 汕头 515063)

一、前言

土壤侵蚀一直都是世界范围内影响人类生存和发展环境的重要问题之一，由于土壤侵蚀导致的水土流失已成为限制许多地方经济发展的主要障碍。从20世界30年代开始，国内外的学者们对土壤可蚀性的研究经历了从研究某种单一因素[1]～[3]到确立可蚀性因子(K)评价指标[4]，最终建立图解法(诺谟图)[5]、经验土壤理化性质测定法[6]或各类预测模型公式[7]～[9]并在实际中加以运用的过程，经典的USLE模型[7]、RUSE模型[8]、EPIC模型[9]等都是对于该问题的重要研究成果。

随着众多学者不断深入地研究侵蚀机理及计算机技术的快速进步，土壤侵蚀预报研究也由一般的因子相关分析向以土壤侵蚀发生过程为基础的过程模型发展。人们以泥沙动力学及河床演变理论为依据，分析侵蚀发生过程中各因子间的力学关系，用较为严密的控制方程计算土壤侵蚀量，出现了一些具有一定物理意义的土壤侵蚀预报模型和实验装置[10]～[12]。

本文从土壤侵蚀模型的重要参数之一——临界剪切应力τc着手，介绍了目前侵蚀测算和泥沙动力学中对该参数的不同理论与计算方法，综合分析现有方法的不足，并指出可能的研究方向及重点领域，以期能为今后的土壤水动力学研究起到一定的借鉴和帮助。

二、临界切应力的概念及其计算

对于土壤，侵蚀的过程就是土壤颗粒在外营力(水力、风力、融冻等)的作用下，分离、搬运、沉积的过程[13]。当土颗粒与土体开始分离的临界状态时，由水体施加给土体的切应力即是临界切应力，以τc表示。

Shields[14]在分析了床面上泥沙颗粒的受力平衡条件后，推导出无粘性均匀沙的临界切应力公式，并在此基础上得出无因次切应力Θc与沙粒雷诺数Re*的关系曲线，其值范围为0.040～0.060[14]。后来学者在Shields的研究基础上陆续提出了一些改进型经验公式，比如Briaud[10]在这基础上通过力学分析和实验，认为τc与平均粒径D50成线性关系，为简化运算在应用中可将τc近似取值为平均粒径D50；美国80年代开始着手研发的被称为WEPP(Water Erosion Prediction Project)[11]的新一代土壤水蚀预报模型最早将临界剪切力(τc)作为直接的参数之一，在模型中使用时通过简单的公式推算取值；Hanson等[12]的JETs实验也提出了基于其实验装置对τc的经验计算方式。

(一)EFA实验

Briaud在文章中指出，只有在水流切应力大于高于临界剪切应力时土颗粒才会发生分离并能观测到一定的冲刷速率[15]，在此分析基础上，Briaud提出将与标准化的小侵蚀速率相对应的剪应力作为临界剪切应力τc的一个可接受的新定义。他定义使用erosion function apparatus(EFA)装置进行为期一周的水波冲刷而仅造成168mm侵蚀时，1mm/hr的速率即是该侵蚀速率标准阈值[15]。

Briaud[16]以理论分析砂和砾石的情况下，冲刷过程是由颗粒的重量控制的，计算τc可看做直接计算克服两个颗粒间摩擦力所需的水流切应力。水平方向受力平衡方程为

τcAe=Wtanφ

其中Ae为水流作用在颗粒上的有效面积；W为土颗粒在水中的重量；φ为两颗粒间的界面摩擦角。若将土壤颗粒视作球形(图3(a))，公式可写作

或

式中α=有效摩擦面积与球形颗粒最大横截面之比，约6.14；D50为代表土壤粒径分布的平均粒径，mm；ρs、ρw为土颗粒的密度，水的密度，g/cm3。

图3 冲刷过程中作用于土颗粒上的力

对于情形如图3(b)时，水对土壤颗粒所施加的合力是平行于侵蚀表面的剪切力，相邻的颗粒不会阻碍这一过程，旋转是围绕着与底层颗粒的接触点进行的。由于分析是针对砂颗粒进行的，因此忽略了颗粒间的电磁力和静电力。在开始运动时，接触点O附近的力矩平衡

τcAea=Wb

或化简可得

对滑动和滚动机制的简单分析有助于阐明影响粗粒土初期运动的重要因素，可以看出临界剪应力τc与平均粒径成线性关系，且其比例系数可能取决于相对密度。这与希尔兹[14]对平坦砂层做一系列水槽实验后所画出的结果图形(the Shields diagram)相一致。通过对于实验数据的对比分析，在粗粒土中临界剪应力τc可以经验性地视作平均粒径D50。

EFA实验是一种简单高效的测试方法，可用标准的取样进行原位测试，但应用范围仅限于侵蚀率在1mm/d(软岩)至数m/h(干净细沙)范围且流速0.1m/s—0.6m/s的情况，实验给出的临界切应力对应于运动的开始和超过这一点的侵蚀率，侵蚀率切(mm/h)切应力(N/m2)的相对误差在10%左右，并不适用于精度要求较高的侵蚀测量或预测使用。

(二)WEPP模型

WEPP模型中，将土壤可蚀性进一步划分为细沟间(interrill)可蚀性(ki)、细沟(rill)可蚀性(kr)和土壤临界切应力τc。其中的细沟侵蚀，就是指由于水流的冲刷力大于临界剪切力而造成的土体分离[17]。Gilley[18]等人通过实验统计了细沟侵蚀与剪切应力之间的经验数据，在对临界剪切应力和土壤特性进行逐步多元回归分析后，发现二者具有显著的线性相关。

对于粘土含量小于7.5%的土壤(soil with water dispersible clay content of less than 7.5%)，

τc=0.216Cla-183(coefficientoflinearextensibility)+0.412ω1.5MPa+0.780

式中Cla为粘粒含量,%；ω1.5MPa为1.5MPa条件下土壤的含水率，%。

对于粘土含量大于等于7.5%的土壤(soils with water dispersible clay content of 7.5% or greater)，

τc=0.296CECCa+1.53Fe+7.75C-11.4CECK-0.535Sand-0.208

式中CECCa为钙含量，cmol/kg；Fe为铁含量，%；C为有机碳含量，%；CECK为钾含量，cmol/kg；Sand 为细沙含量，%。

这种以两个经验公式推算不同土壤临界切应力τc的方法并不是一种基于机理分析而是实验数据分析。事实上为了得到WEPP模型的可蚀性参数，1987年和1988年[19]在全美24个州做了2年人工降雨和放水冲刷试验，但结果并不理想。因为试验得到的土壤流失量难于区分是分离的结果还是搬运的结果。

此后，雷廷武[20]等曾在理论分析的基础上设计了一种测量临界剪切应力的实验装置，用于测量沉积疏松土壤中细沟再生的力学参数并得到与沟坡相关的临界剪切应力测量值。张晴雯[21]利用室内细沟侵蚀模拟冲刷实验，由实验来直接计算细沟侵蚀可蚀性参数及土壤临界抗剪切应力。其认为，对于细沟侵蚀产沙数学模型[22]：

式中Dr为细沟剥蚀分散率，kg·m-2·s-1；Kr为单位宽度上的细沟可蚀性参数，kg·N-2·s-1；τ、τc为水流剪切应力和土壤临界剪切应力，N·m-2；q为流量，m2·s-1；c为泥沙含量，kg·m-3；Tc为水流的输沙能力，kg·m-1·s-1。

当水流中的含沙量c=0时，细沟侵蚀过程具有最大可能剥蚀分散率Dr，max

Dr,max=Kr(τ-τc)

可以看出概念上WEPP基于物理过程，且在计算侵蚀时几乎涵盖了影响土壤侵蚀的各种因素，但一些过程的表达仍是经验公式，对侵蚀机理仍需要进一步研究和验证。WEPP中所需输入的参数τc的确定尚必须采用非测量的“估算”方法，多数情况下需要采用经验数据对所得参数进行率定和修正。因此，在加强典型区域的侵蚀研究的同时，还需要强化土壤侵蚀模型中参数区域规律的研究，建立多重尺度上的模型参数与其相关环境因子的关系。

(三)JET实验

JET(Jet Erosion Test)是一种可用于现场和实验室评估土壤可蚀性的通用实验[23]。Hanson等认为土壤侵蚀速率ε与有效剪切应力τe和临界剪切应力τc的差值成正相关[24]。

ε=Kd(τe-τc)

式中ε为可蚀性系数，m3/N-s；τe为有效剪切应力，Pa；τc为临界剪切应力，Pa。

图2 JET实验示意图与参数定义

实验中，临界剪切应力τc主要是根据平衡冲刷深度Je确定的，其表达式为:

式中τ0为喷嘴处射流速度引起的最大应力，Pa；Jp为等速核长度，m；Jp为平衡冲刷深度，m；U0为喷嘴处的速度，m/s；g为重力加速度常数，m/s2；h为水头差，m。通过实验测量所需数据，代入式中即得出侵蚀的临界剪切应力[24]。

综上所述，不论是哪种预测模型，在计算土壤侵蚀率或可蚀性时临界切应力τc作为一种计算可蚀性的必要参数，在对其进行处理时，都是以实验回归分析和实验经验分析得出，并简化了坡度、颗粒均匀性等因素的影响。最终计算出的土壤可蚀性与真实结果有着一定的误差，需要在每次不同的实际应用时进行相应的模型修正。

三、临界切应力的理论分析计算方法

在泥沙动力学中，泥沙颗粒由静止进入运动状态的过程称为泥沙的起动[25]，是泥沙动力学研究的基本问题之一，对于临界切应力τc又被称为起动切应力[26]，在国内外学者中都有广泛的研究。

Engelund[27]在研究水流阻力时得到的规律

Θ′=0.06+0.4Θ2

其中Θ′与Θ分别是沙粒阻力与总阻力有关的无因次切力，随着Θ的减小，Θ′趋向于定值0.06，因此Θc=0.06可认为相当于泥沙的起动条件，此时的水流切应力即为临界切应力τc。

叶基阿扎洛夫[28]对Shields的结果作了论证，建立颗粒的平衡条件，并假设泥沙起动时，颗粒的作用流速等于颗粒的自由沉降速度，公式变换可得

对于粗泥沙，粗糙紊流，χ=1，颗粒绕流阻力系数CD=0.4。取Ks=d，y=0.63d，代入上式可得Θc=0.0616≐0.06。

爱因斯坦在研究推移质输沙率时[29]，将上举力看做随机变量，泥沙起跳概率即是上举力FL大于颗粒重力W的概率P(W/FL<1)，颗粒的起跳条件公式可改写为

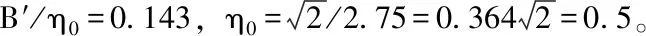
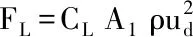
τc=0.715(γs-γ)d

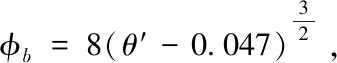
当gb=0时或φb=0时，得θ′=Θc=0.047。这一结果已为许多研究者所引用，如格斯勒在研究非均匀沙的起动条件时[31]，取个别颗粒的起动条件是Θc=0.047；万兆惠在研究泥沙起动条件时也采用了这一结果[32]。

相对于国外的研究，国内学者起步较晚。褚君达[33]对国内外数十种不同形式的泥沙起动公式进行了分析，统一转化为无量纲起动切应力Θc=τc/(γs-γ)D(τc为水流施加的临界切应力，γs和γ分别为泥沙、水的容重，D为泥沙粒径)的形式，并计算得出无粘性均匀沙的Θc为0.0231～0.0716；何文社[34]从推移质泥沙起动的特点出发，引入附加质量力，采用滚动起动模型推导出了泥沙起动无因次切应力起动公式，结果表明弱动(个别运动)情况下无因次切应力为0.0291～0.0582，中动(少量运动)的情况下为0.353～0.706；

解刚等[35]考虑了水流条件及床沙组成对泥沙起动的影响，采用滚动起动模型推导出了非均匀沙分级起动的切应力公式:

式中di为分级粒径，mm；α为系数，可取α=2/3；η为床面起动流速与切应力间的关系系数，可取η=7.055；dm为平均粒径。

黄伟[36]等以长江口取样的细颗粒泥沙为样本进行了环形水槽起动试验，给出3组不同中值粒径泥沙的起动流速和临界起动切应力公式，同时用湍动能法估算了不同含沙量水体的床面切应力，给出了泥沙起动过程中床面切应力与含沙量之间的关系式，得出中值粒径为0.082mm、0.035mmhe 0.008mm的泥沙起动流速分别为0.29m/s、0.55m/s和0.78m/s，临界切应力分别为0.19Pa、0.34Pa、0.46Pa。可见中值粒径在0.1mm以下的细颗粒泥沙，临界切应力和起动流速随着粒径的增大反而减小(即粒径越大，越容易起动)。

四、结论与展望

(1)目前在计算土壤侵蚀时，工程应用中对于土壤侵蚀的临界切应力计算主要是利用经验公式或实验模型进行，因此方法本身存在一定的误差，对于如何找到更准确表征临界切应力的计算方法将是一项长期任务。

(2)相对于各类侵蚀预测模型的经验计算方法，泥沙动力学中对于临界切应力的研究更注重侵蚀过程的机理分析，但主要是借鉴明渠水流参数进行。由于坡面侵蚀发生条件及过程复杂，径流特征与明渠水流存在较大差异，研究结果带有一定的不确定性。未来研究中影响因素设定有复杂化、全面化的趋势，从而以更准确的径流水动力机制的角度解释土壤侵蚀的发生和发展。

(3)目前大多研究所获得的结论都是整个坡面的平均状况，对于复杂坡面侵蚀演化过程中的分布规律及其特性研究十分稀少，是今后研究中的重要内容。

(4)加强解析计算方法与实际工程的结合，特别是应加强土壤侵蚀水动力学特性的原位研究，以更好地揭示土壤侵蚀水动力特性的变化规律。