主成分分析方法在煤灰特性分析能力验证结果综合评价中的应用

(中国船舶重工集团公司第七二五研究所(洛阳船舶材料研究所)，洛阳 471023)

1 引言

随着检验检测行业迈入高质量、快速、健康发展的新时代，行业监管愈发严格，市场竞争愈发激烈，促使各检验检测机构愈发重视内外部的质量控制，更加积极、主动地参与国内外实验室间比对活动。能力验证是实验室间比对活动的典型代表，既是确保实验室检测能力与质量水平的有效手段，也是申请和维持中国计量认证(CMA)、中国合格评定国家认可委员会(CNAS)、美国“国家航空航天和国防合同方授信项目”(NADCAP)等国内外实验室认证认可检验检测资质的基本要求。

目前，能力验证通常采用Z比分数评价单一参数的测量值与实验室间统计平均值(公认值)的一致性，缺乏行业公认的多参数检测能力综合评价的方法和手段。能否采用各参数的Z比分数的平均值来进行综合评价呢？由于具体参与实验室在参加多参数的能力验证试验过程中，或采用同一标准方法、检测设备、测量程序来测量数个相似的参数，其引入的误差可能具有同向性，从而使这些参数的Z比分数存在一定程度的相关性。在参数间存在较强相关性时，若不考虑参数间相关性引起的权重差异，对多参数的Z比分数通过简单加和或平均的方法评价实验室的综合检测能力是不科学的。

主成分分析是应用统计学中常用的多元统计分析方法[1]，广泛应用于环境污染评价[2-4]、区域社会经济评估[5，6]、产品特性分析[7]等领域的多参数综合评价。为解决能力验证活动多参数综合评价的问题，文献[8-10]分别以食品检测[8]、小麦品质检验[9]、钛合金成分分析[10]三个能力验证活动为例，引入主成分分析法对参与实验室的检测能力进行综合排序，为多参数能力验证结果的综合评价提供了新的研究思路。

本文以煤灰特性分析能力验证为例，采用SPSS 21.0软件，探讨了主成分分析法在多参数能力验证结果综合评价中的具体应用，以期为能力验证提供商和参与实验室进行全面、科学的综合评价提供参考案例。

2 材料和方法

2．1 材料

数据来源于CNAS T0517煤灰特性分析能力验证中的10项化学成分与4项温度性能测量参数。不考虑缺项实验室，仅对全部参与上述14项常规测量参数的24家实验室(依序命名为L01～L24)的测量结果进行主成分分析与综合检测能力评价。

能力验证常采用标准化后的测量结果(Z比分数)作为单个测量参数检测能力水平的评价指标，越接近0表示检测能力越好。国内的主流评价原则如下[11]：|Z|≤1表示测量结果有很好的准确度；1<|Z|≤2表示测量结果有较好的准确度；2<|Z|<3表示有问题结果；|Z|≥3表示“不满意”结果(离群值)。根据上述评价原则，暂不考虑正负符号的影响，将Z比分数取绝对值(|Z|)作为主成分分析的数据来源，详见表1。表中DT、ST、HT、FT分别为变形温度、软化温度、半球温度、流动温度。

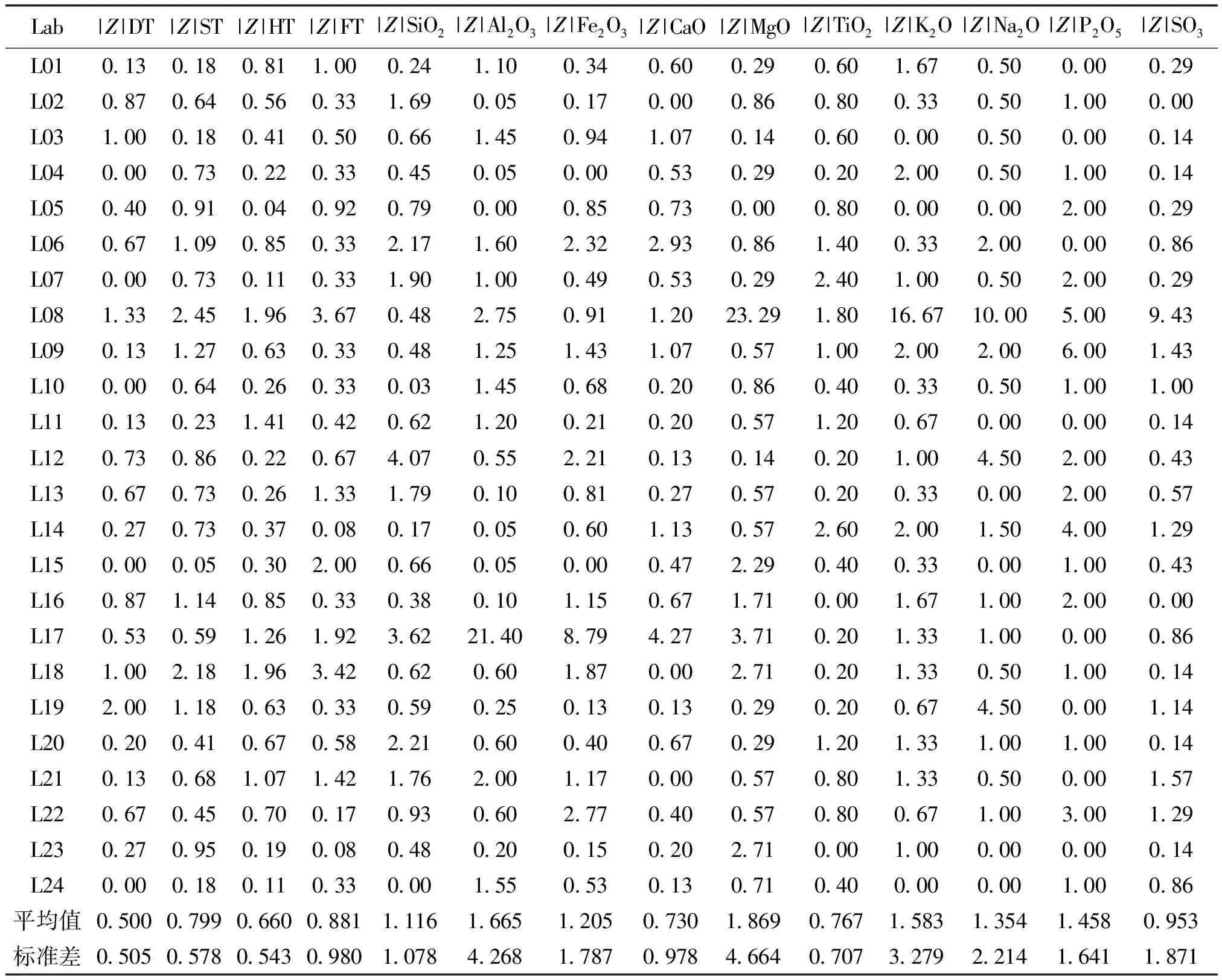
表1 24家实验室的|Z|比分数

2.2 方法

主成分分析利用正交变换将可能存在相关性的一组变量通过线性组合，转换为线性不相关的一组变量(主成分)，并确定各原始变量及主成分的权重系数。通过m个主成分代替p个原始变量的信息(m≤p)，从而排除原始变量中重叠(相关)的信息(部分)，实现数据降维、识别关键因子的目的。

基本步骤如下：(1)标准化原始数据，以消除量纲因素的影响(本文采用Z比分数，不涉及此步骤)。(2)计算各原始参数的相关性矩阵，并执行KMO检验和Bartlett球形检验，以确定该系列数据是否适用于主成分分析。(3)计算主成分分析方差分解表，确定保留的m个主成分数量。m取值一般符合以下两个条件：所提取m个主成分的特征值的方差累积贡献率应≥80%，特征值λi宜≥1。(4)进一步计算主成分的旋转后因子载荷矩阵(采用最大方差法)获得各参数载荷值(权重系数)。(5)对m个主成分进行加权求和，并对各参数的权重系数进行归一化，得到综合主成分F的计算模型。

本文利用SPSS 21.0“降维-因子分析”功能进行主成分分析。主要过程及参数设置如下：(1)描述：统计量显示原始分析结果，计算相关矩阵系数，执行KMO和Bartlett的球形度检验；(2)抽取：方法选择主成分，分析相关性矩阵，基于特征值大于1抽取主成分；(3)旋转：选择最大方差法，输出旋转解。其中，最大收敛性迭代次数设定为25。

3 结果与分析

3.1 适用性分析

利用SPSS计算表1数据中各参数间的相关系数，列于表2。由表2，91个相关系数中(不含自相关系数)有35个相关系数大于0.4，表明这些变量有正相关性，其中14个相关系数大于0.6，表明这些变量存在强正相关性，存在很大程度的信息重叠。

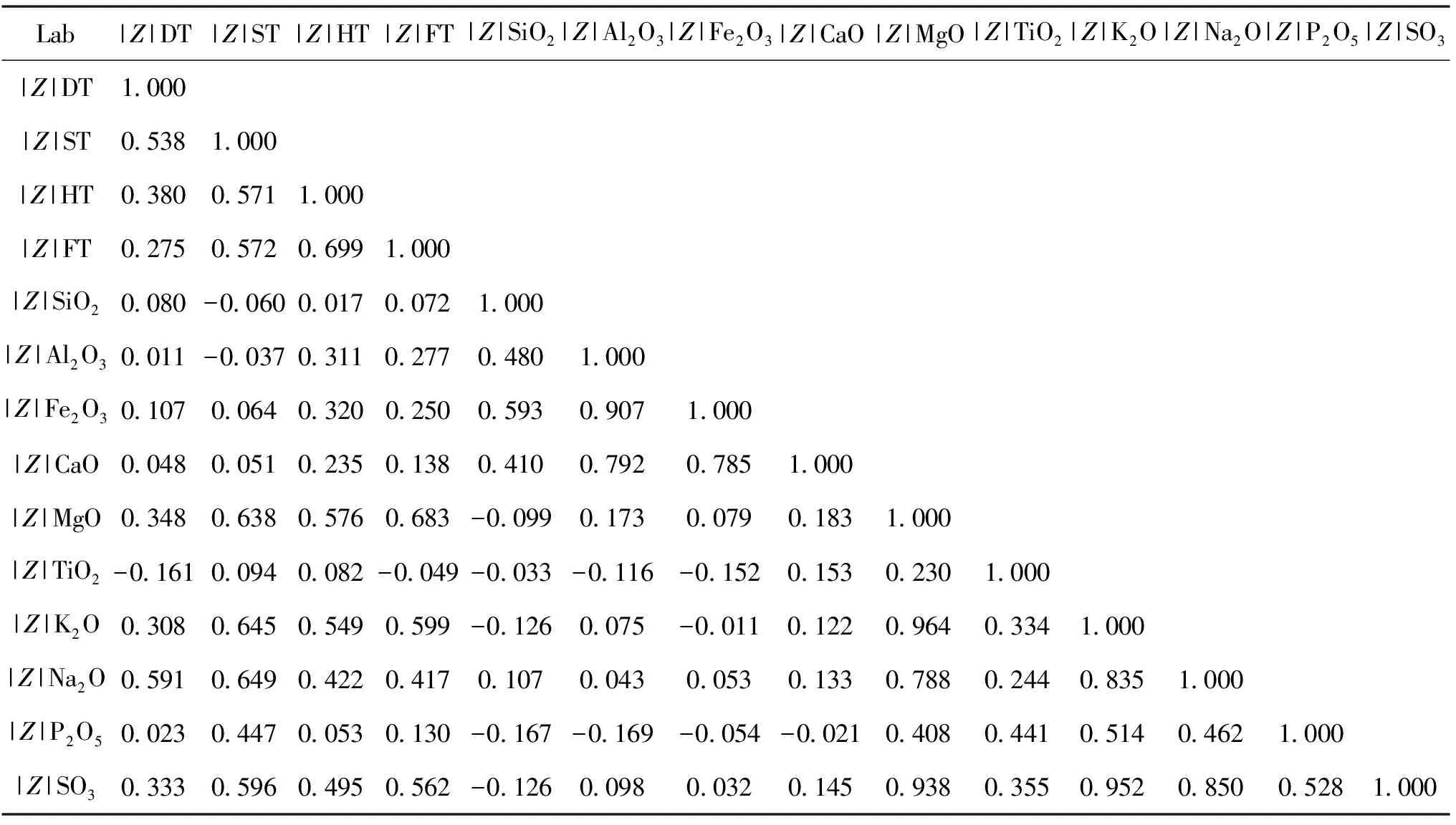
表2 13个参数的相关系数矩阵

执行KMO检验和Bartlett球形检验，结果见表3。KMO统计量为0.664，Bartlett球形检验显著性(sig.)小于0.01。综上，原始变量适合主成分分析。

表3 KMO统计量和Bartlett检验表

3.2 主成分的确定

利用SPSS执行因子分析，计算主成分分析方差分解表(表4)，并绘制碎石图(图1)。由表4，前4个主成分的特征值均大于1，方差累积贡献率达81.2%，原有变量的信息丢失较少，因子分析效果较理想。结合图1曲线斜率变化，前4个主成分的坡度较大，后逐渐趋于平缓。综上，保留前4个主成分。

表4 主成分的特征值、方差率(贡献率)和累积贡献率

图1 主成分特征值随主成分数的变化关系图

3.3 线性表达式

采用最大方差法进一步计算主成分的旋转后因子载荷矩阵(表5)。

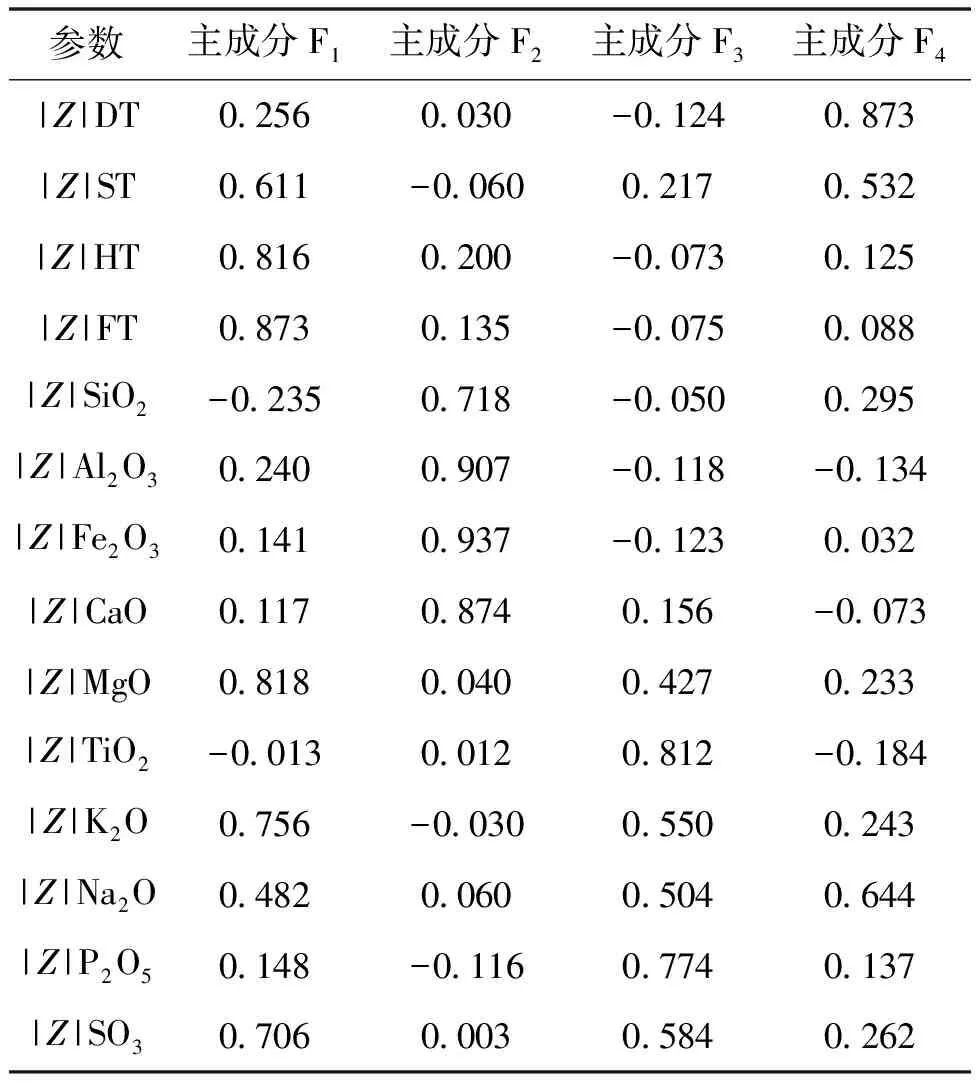
表5 保留主成分对应的载荷矩阵

由表5，得到4个主成分的线性表达式(公式1～4)：

F1=0.256ZDT+0.611ZST+0.816ZHT+0.873ZFT-0.235ZSiO2+0.240ZAl2O3+0.141ZFe2O3+0.117ZCaO+0.818ZMgO-0.013ZTiO2+0.756ZK2O+0.482ZNa2O+0.148ZP2O5+0.706ZSO3

(1)

F1=0.030ZDT-0.060ZST+0.200ZHT+0.135ZFT+0.718ZSiO2+0.907ZAl2O3+0.937ZFe2O3+0.874ZCaO+0.040ZMgO+0.012ZTiO2-0.030ZK2O+0.060ZNa2O-0.116ZP2O5+0.003ZSO3

(2)

F1=-0.124ZDT+0.217ZST-0.073ZHT-0.075ZFT-0.050ZSiO2-0.118ZAl2O3-0.123ZFe2O3+0.156ZCaO+0.427ZMgO+0.812ZTiO2+0.550ZK2O+0.504ZNa2O+0.774ZP2O5+0.584ZSO3

(3)

F1=0.873ZDT+0.532ZST+0.125ZHT+0.088ZFT+0.295ZSiO2-0.134ZAl2O3+0.032ZFe2O3-0.073ZCaO+0.233ZMgO-0.184ZTiO2+0.243ZK2O+0.644ZNa2O+0.137ZP2O5+0.262ZSO3

(4)

3.4 主成分的实际意义

该煤灰的SiO2、Al2O3、Fe2O3、CaO、MgO、TiO2、K2O、Na2O、P2O5、SO3含量统计中位值分别为47.97%、21.11%、24.50%、2.20%、0.74%、0.86%、0.84%、0.34%、0.24%、0.39%，结合表5、公式1～4归纳得出4个主成分所能代表的典型参数(表6)。

表6 主成分对应的典型评价参数表

3.5 综合排序

按各主成分Fi所对应的特征值λi占所提取的全部4个主成分特征值之和的比例作为权重对4个主成分进行加权求和(公式5)，得到(归一化前)综合主成分F′的线性表达式(公式6)。

(5)

F1=0.197ZDT+0.365ZST+0.464ZHT+0.471ZFT+0.100ZSiO2+0.342ZAl2O3+0.315ZFe2O3+0.314ZCaO+0.498ZMgO+0.091ZTiO2+0.465ZK2O+0.383ZNa2O+0.159ZP2O5+0.456ZSO3

(6)

进一步令所有参数的权重之和为1，对各参数的权重系数进行归一化，得到(归一化后)综合主成分F的线性表达式(公式7)。其中，HT、FT、MgO、K2O、SO3的权重较大。

F1=0.043ZDT+0.079ZST+0.100ZHT+0.102ZFT+0.022ZSiO2+0.074ZAl2O3+0.068ZFe2O3+0.068ZCaO+0.108ZMgO+0.020ZTiO2+0.101ZK2O+0.083ZNa2O+0.034ZP2O5+0.099ZSO3

(7)

按公式7计算各实验室的综合主成分得分及排序，数据见表7。综合主成分F代表了参与实验室的综合检测能力，F越接近于0，表示综合检测能力越强。由表7，参考Z比分数的评判原则[11]统计综合主成分得分的分布情况，上述24家实验室的综合主成分得分F≤1、1

表7 24家实验室的主成分得分与综合能力排序表

4 结论与讨论

本文以煤灰特性分析能力验证为例，探讨了主成分分析在多参数能力验证果综合评价中的应用。在基本保留原有数据信息的基础上，通过合理降维，将10项化学成分、4项温度性能共14个具有潜在相关性的Z比分数提取为4个相互独立的主成分，并进一步加权求和获得综合主成分的线性表达式，计算了24家实验室的综合主成分得分与排序。主成分分析依据各参数自身数据的相关性和变异性客观的赋予各参数权重，具有较好的科学性和严谨性，是现行能力验证单参数评价方法的有效补充。

由于多参数能力验证综合评价的复杂性，主成分分析综合评价方法亦存在部分未能解决的问题[10]。例如：(1)缺项实验室的综合能力尚缺乏科学有效的评估方法；(2)文中采用绝对值化的|Z|统计量，丢失了多参数Z比分数的正、负符号信息，无法评估误差的性质及潜在的系统误差的方向性差异。该问题的解决尚需要进一步研究与发展更加科学、全面的多参数能力验证综合评价方法；(3)本文仅考虑“纯粹”的检测能力，将各参数的社会、经济、工程价值或意义视为“同等地位”，而忽略了其实际应用价值或意义的差异性；必要时应结合“专家调查权重法”对原始变量参数的权重进行适当的调整。

综上所述，主成分分析在一定程度上为多参数能力验证提供了较科学、客观的综合评价方法，建议经过更广泛的探讨和研究后，酌情纳入多参数能力验证评价体系。