Improved adaptive filter and its application in acoustic emission signals

Wang Jiajun Xu Feiyun

(School of Mechanical Engineering, Southeast University, Nanjing 211189, China)

Abstract：In order to de-noise and filter the acoustic emission (AE) signal, the adaptive filtering technology is applied to AE signal processing in view of the special attenuation characteristics of burst AE signal. According to the contradiction between the convergence speed and steady-state error of the traditional least mean square (LMS) adaptive filter, an improved LMS adaptive filtering algorithm with variable iteration step is proposed on the basis of the existing algorithms. Based on the Sigmoid function, an expression with three parameters is constructed by function translation and symmetric transformation.As for the error mutation, e(k) and e(k-1) are combined to control the change of the iteration step. The selection and adjustment process of each parameter is described in detail, and the MSE is used to evaluate the performance. The simulation results show that the proposed algorithm significantly increases the convergence speed, reduces the steady-state error, and improves the performance of the adaptive filter. The improved algorithm is applied to the AE signal processing, and the experimental signal is demodulated by an empirical mode decomposition (EMD) envelope to obtain the upper and lower envelopes. Then, the expected function related to the AE signal is established. Finally, the improved algorithm is substituted into the adaptive filter to filter the AE signal. A good result is achieved, which proves the feasibility of adaptive filtering technology in AE signal processing.

Key words：acoustic emission;adaptive filtering; envelope demodulation; least mean square (LMS) algorithm; variable iteration step

The phenomenon of rapid release of local energy in materials is called acoustic emission (AE). The deformation and crack expansion of the material under stress are the important mechanisms of structural failure.Acoustic emission technique (AET) is a detection technique[1], which uses sensors to collect acoustic emission signals, and uses instruments to analyze and process acoustic emission signals and to infer the position and state of an acoustic emission source. It is advanced nondestructive testing technology, and has been applied in the petroleum chemical industry, power industry, aerospace, transportation and so on.Acoustic emission detection technology involves acoustic emission sources, wave propagation, and the conversion of the signal and data acquisition. Through the acquisition of acoustic emission signals, the characteristics of acoustic emission sources and the development of generation and movement of the materials can be obtained. The acoustic emission signals are usually collected using the sensors, and the noise interference in the acquisition process will have a great influence on the detection result[2], so it is necessary to filter the noise of the acoustic emission signal collected.

In the field of acoustic emission, the common filtering techniques are hardware filtering and software digital filtering[3].Hardware filtering means inserting filters in the proper location of the whole circuit system, such as the main amplifier, to select the appropriate “frequency window”. The characteristic of software digital filter is that it is flexible and convenient to use and powerful. Wavelet transform plays an important role in acoustic emission signal filtering and noise reduction. Zhao et al.[4]used wavelet analysis to reduce noise interference and improve the ability to identify and judge the nature of acoustic emission sources. In terms of the fact that the traditional linear filtering method is not ideal, Zhou et al.[5]proposed an improved method using Donoho to produce the threshold of de-noising. The software filter and the hardware filter are, respectively, used to de-noise the AE signals.Aimed at the problems of noise polymorphism and randomness during the transmission and acquisition of acoustic emission signals, the combination of morphological filtering and the ensemble empirical mode decomposition (EEMD) are proposed by Xi et al.[6], which de-noise signals from different angles in space and time domains.On the basis of the minimum entropy deconvolution (MED) and the maximum correlated kurtosis deconvolution (MCKD), an improved MCKD noise reduction method[7]based on a bidirectional cyclic restructure filtering criterion is proposed.

Adaptive filtering technology also plays an important role in acoustic emission signal processing. An adaptive filter is a filter that can be adjusted adaptively by a parameter (or coefficient), so that the filter output can minimize a particular target function containing the reference signal as far as possible. The common adaptive filtering algorithms[8]contain the LMS algorithm, LMS Newton algorithm, normalized LMS algorithm and recursive least square (RLS) algorithm.

In this paper, an improved variable iteration step LMS algorithm is proposed and used to process acoustic emission signals. At the same time, its performance in the simulation function and AE signals is compared in order to show its feasibility and advantages.

1 Principle and Performance Analysis of LMS Algorithm

1.1 Principle of classical LMS algorithm

The LMS algorithm is a search algorithm which modifies the parameters by objective function to simplify the computation of gradient vectors. Djendi et al.[9]focused on the application of adaptive filter based on the LMS algorithm. Zhu et al.[10]used the LMS algorithm to solve the problem of stereophonic echo cancellation field (SAEC). Kay[11]realized the adaptive filter using a linear combiner, and the optimal solution of the parameters under the condition of multiple input signals was derived. This solution minimized the mean square error when estimating the reference signald(k). The optimal Wiener solution is

w0=R-1p

(1)

whereR=E[X(k)XT(k)]andp=E[d(k)X(k)], so the main flow of the LMS algorithm is

(2)

1.2 Convergence properties of LMS algorithm

For a FIR filter with unknown coefficient vectors, the convergence of the filter[12]can be obtained as

(3)

whereλmaxis the maximum eigenvalue ofR. The more iterations there are, the closer to the Wiener solution the solution will be.

1.3 Principle of variable iteration step LMS algorithm

The traditional LMS algorithm is the most classic and widely used algorithm in the field of application, but there is a great contradiction between the steady state error and the convergence speed. The smaller iteration step can obtain a small steady state error, but the convergence speed is slow, and the larger iteration step can obtain a larger convergence speed, but the steady-state error cannot be guaranteed. Therefore, many improved LMS algorithms have been proposed by scholars at home and abroad. Qin et al.[13]proposed a variable iteration step LMS algorithm based on Sigmoid function, but it is not perfect, and the change of step size is more obvious.

(4)

The normalized LMS algorithm[14]adjusts the iteration step through a certain normalized function form of the input signal. Its iterative formula is

(5)

where ‖x(k)‖2represents the square norm of the input signal. Paleologu et al.[15]proposed a bilinear form for the normalization algorithm. Batista et al.[16]applied the NLMS algorithm to sparse interpolation, and it achieved good results. Chen et al.[17]proposed an improved algorithm based on Sigmoid function,

(6)

It has greatly improved the convergence speed, convergence accuracy, steady state error and the anti-noise performance, but it increases the computational complexity and the algorithm complexity.In Ref.[18], an improved LMS algorithm, RELMS algorithm, is proposed. The following formula is used to improve the convergence accuracy and steady state error of the LMS algorithm by using the adjacent error as the update iteration basis.

w(k+1)=w(k)+2β[1-exp[-αe(k)e(k-1)]]

(7)

Zhang et al.[19]proposed an algorithm on the basis of the SVSLMS algorithm. By establishing a new iteration step and the nonlinear function model of error, five parameters are introduced to make the iteration step controllable.However, the error mutation is not taken into account.

(8)

On the basis of the MVSS-LMS algorithm, Lü et al.[20]increased the forgetting weighting and estimation of historical errors and controlled the update of the iteration step. At the same time, the improved algorithm dynamically controls the updating range of the iteration step, and reduces the computational complexity by using the sliding window forgetting weighting.

(9)

μ(k+1)=λμ(k)+γ[e(k)e(k-1)+p2(k)]2

(10)

The above algorithms improve iteration performance to a certain extent, but the applicability and iteration speed are not so good, and the flexibility of parameter adjustment is not good enough. In order to process more complex signals and to cope with sudden error changes, an improved variable iteration step LMS algorithm is proposed.

2 Improved Variable Iteration Step LMS Algo-rithm

2.1 Principle of the algorithm

It can be seen from Fig.1 that the value of the function increases with the increase of the absolute error value, which is in agreement with the expectation of the larger iteration step when the error is larger in the LMS algorithm. That is, the iteration step will increase accordingly when the error is large.

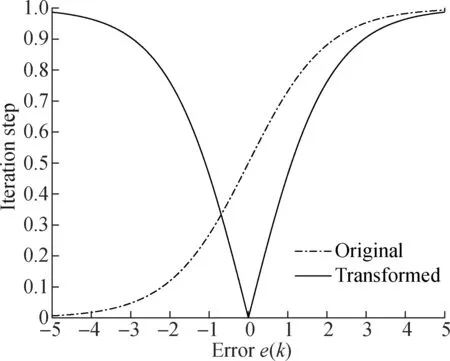
Fig.1 Transform of Sigmoid function

In order to make the nonlinear function of the iteration step and error more variable and adjustable,parametersα,β,γare introduced into it to control the shape of the function.γis a parameter introduced to avoid large changes in the step size when the function converges, and the odd number is taken by default.On this basis, the errore(k) is combined withe(k-1) to change the size of the iteration step. Therefore, an improved variable iteration step LMS algorithm is proposed as

(11)

2.2 Performance analysis

First, the influence of each parameter is studied. From Fig.2, we can clearly see that the range ofβcontrols the iteration step. The value of iteration step function increases with the increase ofβ. Therefore, the largerβcan obtain a faster convergence rate. Fig.3 shows the influence ofα.

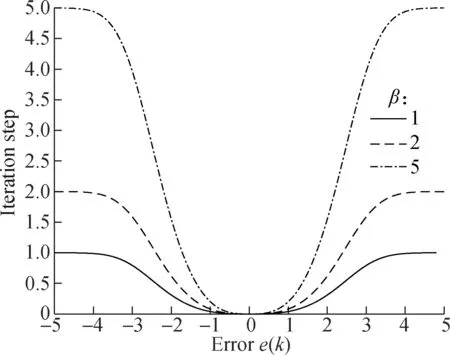
Fig.2 The effect of β

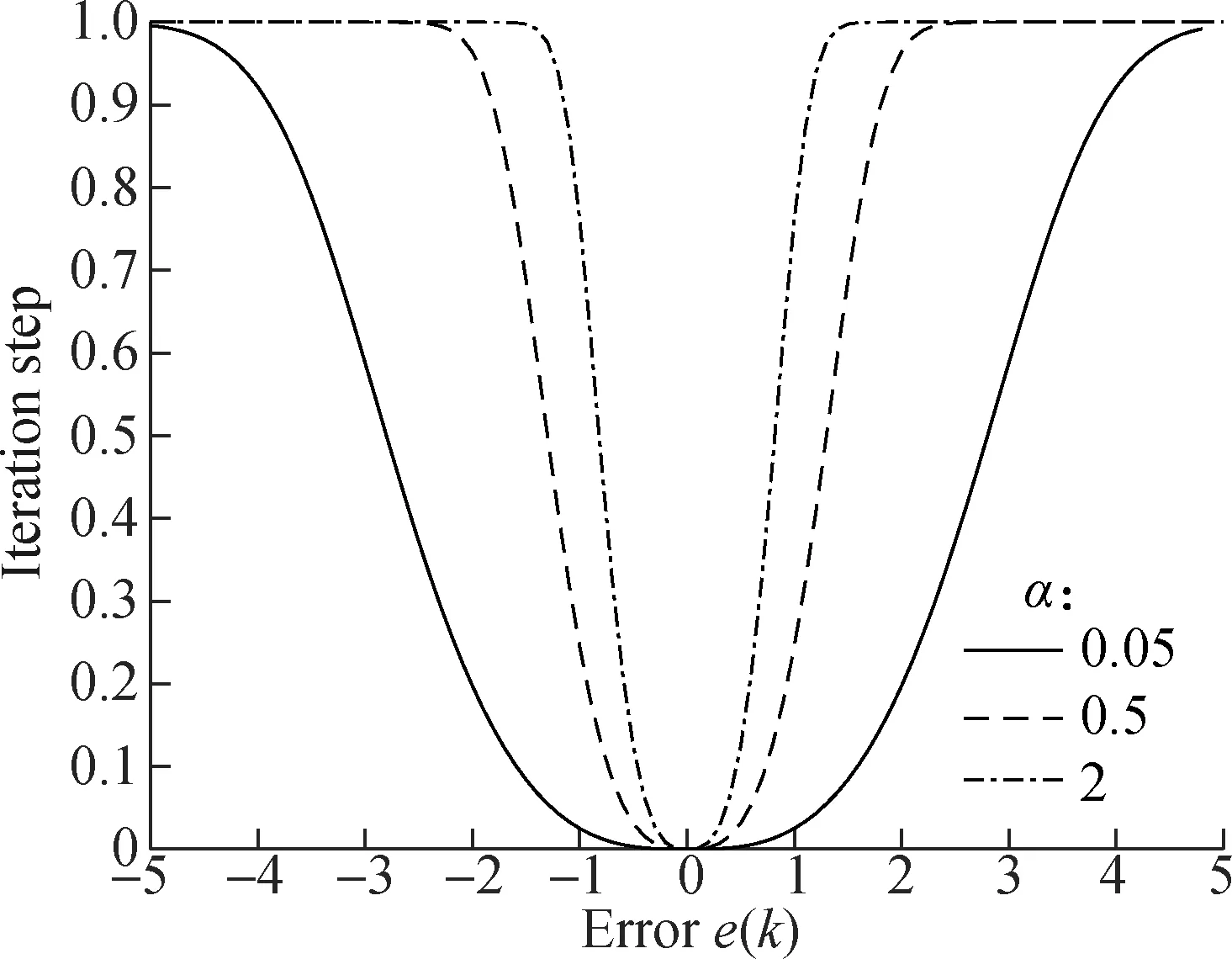
Fig.3 The effect of α

It can be clearly seen from Fig.3 thatαcontrols the shape of the function. The oversize value will lead to the iteration step approaching to 1, which is not conducive to the adaptive-adjustment of the iteration step. Therefore,αshould be kept within a small range. Fig.4 shows the influence ofγ.

Fig.4 The effect of γ

From Fig.4, it is clear that the performance of the iteration step function is the best when the value ofγis 3. With the change in the error, the iteration step function can be changed as well, thus avoiding the large change of the iteration step when the function converges.

2.3 Simulation analysis

Simulation function is constructed as

y=sin(2π10t)+sin(2π20t)+sin(2π30t)+n(t)

(12)

In order to better distinguish the filtering effect of the variable iteration step LMS algorithm, the amplitude of the first half of the white noise is 2, the second half is uniform white noise, and the simulation analysis is carried out through MATLAB. The performance of the algorithms is measured by comparing the MSE (mean square error). First, the algorithm is compared with the traditional LMS algorithm. The simulation results are shown in Fig.5.

(a)

(b)

(c)

Then, the algorithm is compared with the current algorithms (Algorithms in Refs.[17-19]). We use the signal-noise ratio (SNR) and MSE to describe the performance of the algorithm. The SNR of each algorithm is shown in Tab.1.

The MSE of learning curve is shown in Fig.6. From Tab.1 and Fig.6, we can clearly see that the SNR of the improved variable iteration step LMS algorithm is the largest of the algorithms. The algorithm is equivalent to the other algorithms in the convergence speed, but it has obvious advantages over the other three algorithms in MSE. For this reason, the improved iteration step LMS algorithm is effective. It can improve the convergence rate and reduce the steady-state error of the iteration.

Tab.1 Comparison of SNR dB

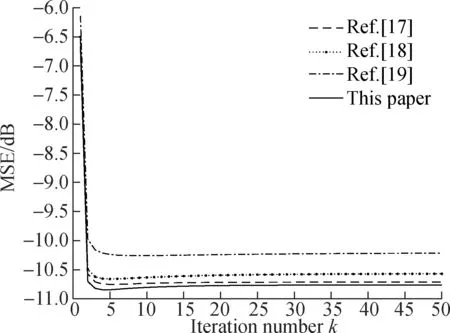
Fig.6 Comparison of the learning curve>

3 Adaptive Filter of Acoustic Emission

3.1 Construction of expectation function

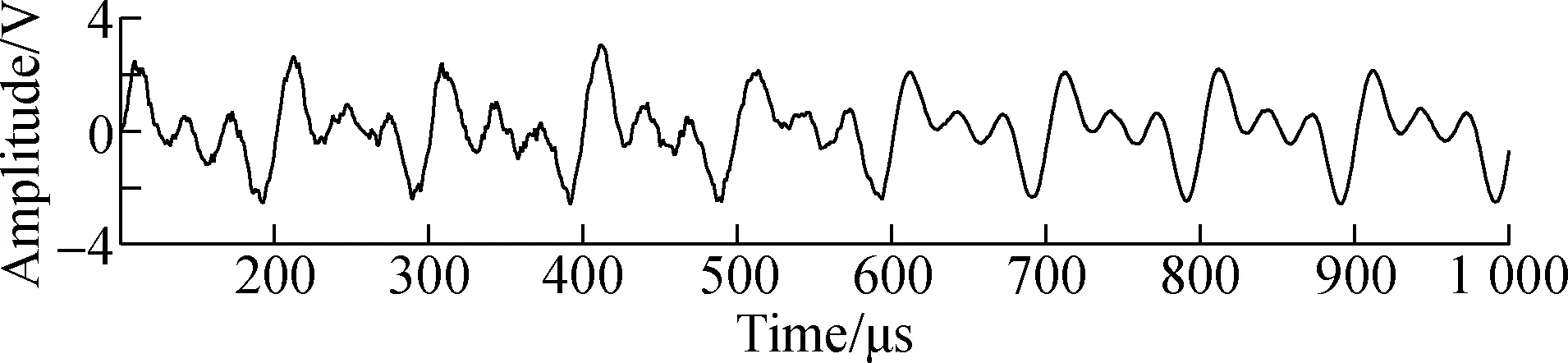
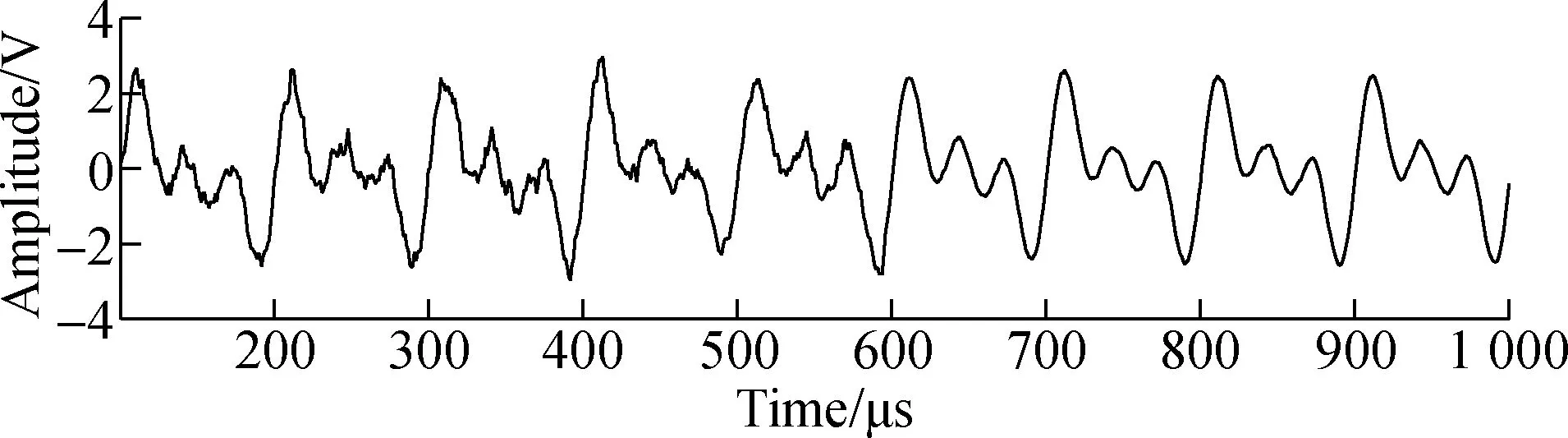
The process of signal processing mainly includes signal preprocessing, sound source positioning, acoustic emission feature extraction and pattern recognition. For this purpose, some redundant noise signals are removed, so that it has good performance in frequency domain processing, thus better source location has become the focus of research. Adaptive filtering technology can filter different acoustic emission characteristics according to different acoustic emission signals. From the time domain morphology of acoustic emission signals, it is generally divided into two basic types: Burst acoustic emission signal and continuous acoustic emission signal. Burst signals are separable waves in the time domain, and are usually separated into acoustic emission signals and noise signals. At present, most of the acoustic emission signals are burst signals. Only when the frequency of acoustic emission signals cannot be separated in the time domain, will it be displayed by continuous signals.A typical burst acoustic emission signal is shown in Fig.7.

From Fig.7, we can observe that the acoustic emission signal is a kind of constant attenuation signal in the time domain. To this end, a desired function with attenuation characteristics can be constructed by the acoustic emission signal, and the acoustic emission signal is filtered by adaptive filtering technology.In view of this characteristic of acoustic emission, we construct the expected functions of the adaptive filter by constructing the corresponding envelope curve and envelope demodulation, so as to realize the filtering processing of the acoustic emission signal.

Fig.7 Acoustic emission signal

The empirical mode decomposition EMD algorithm is a new method for nonlinear and non-stationary data analysis proposed by Huang[21]. This paper uses EMD envelope demodulation to construct the upper and lower envelopes of acoustic emission signals.The steps are as follows：

1) Calculate all local extremum points ofx(t).

2) Work out the upper envelopeu(t) and the lower envelopev(t).

3) Work out the meanm(t)=(u(t)+v(t))/2 and the differenceh(t)=u(t)-v(t).

4) Judge whetherh(t) satisfies two properties of intrinsic mode function (IMF)[22]. If so,h(t) becomes IMF, else repeat steps 1) to 3) untilh(t) satisfies the properties of IMF, then it is recorded asc1(t).

5) Taker1(t)=x(t)-c1(t), repeat steps 1) to 4) untilrn(t) is a monotone signal or the value ofrn(t) is less than the given threshold.x(t) can be shown as

(13)

Through the above EMD method, the upper and lower envelopes of acoustic emission signals can be obtained. A new method for constructing the expected function of acoustic emission signals is established. When the amplitude is greater than 0, the upper envelope curve is used as the expected functiond(k). When the amplitude is less than 0, the lower envelope curve is used as the expected functiond(k).

3.2 Experimental analysis

The experimental data is provided by the Donghua Special Equipment Research Institute. The condition is shown in Tab.2. The arrangement of sensors is shown in Fig.8.

Tab.2 Experimentalconditions

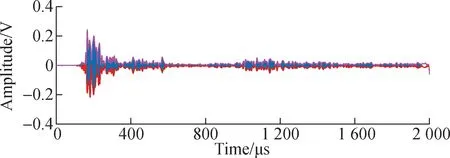
Single strike is the generation of AE signal.The distance from the sensors is 150 mm.Then the experimental original signal is obtained, and its envelope demodulation and adaptive filtering are carried out, in which the adaptive filter parametersα=5,β=0.2,γ=3. The results are shown in Fig.9. The learning curve of the experimental signal is shown in Fig.10.

Fig.8 Sensors arrangement

(a)

(b)

(b) Adaptive filtering signal

Fig.10 Learning curve

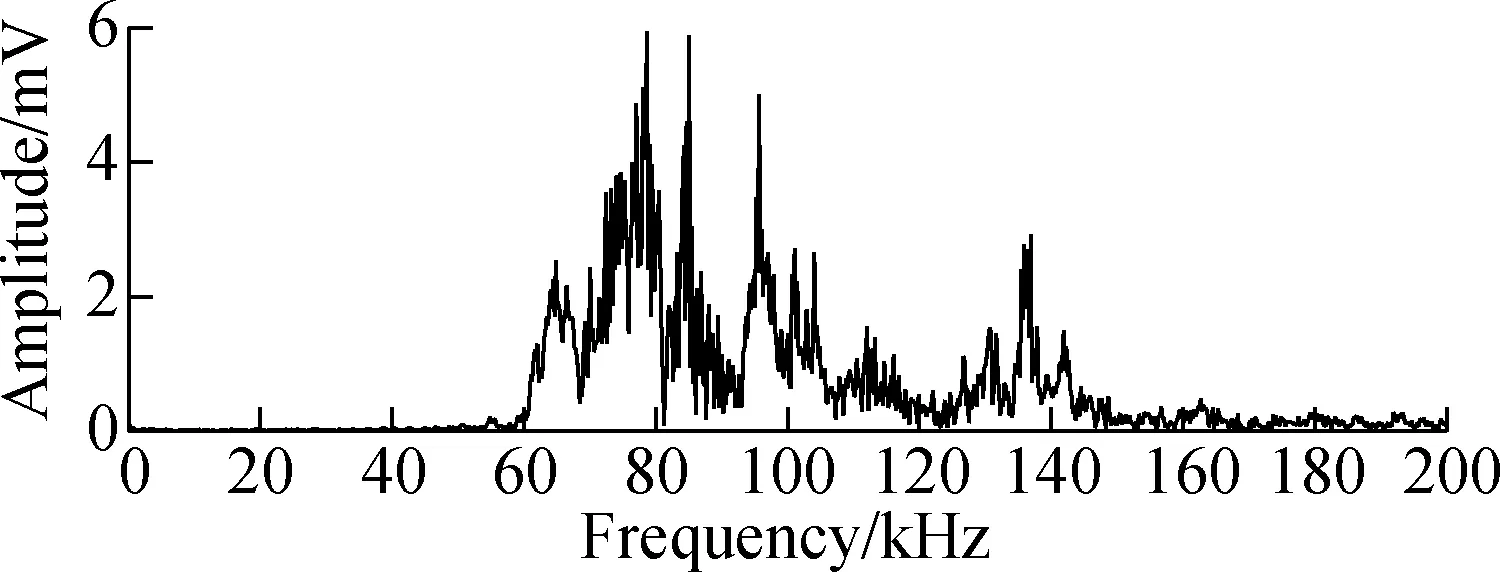
In the frequency domain, it can be seen from Fig.11 that the algorithm weakens the sub peaks on the edges of the main edges of the spectrum,so we can clearly find the main peak(around 80 kHz).

3.3 Performance of the algorithm applied to acoustic emission signals

3.3.1 Influence of the parameters on the learning curve

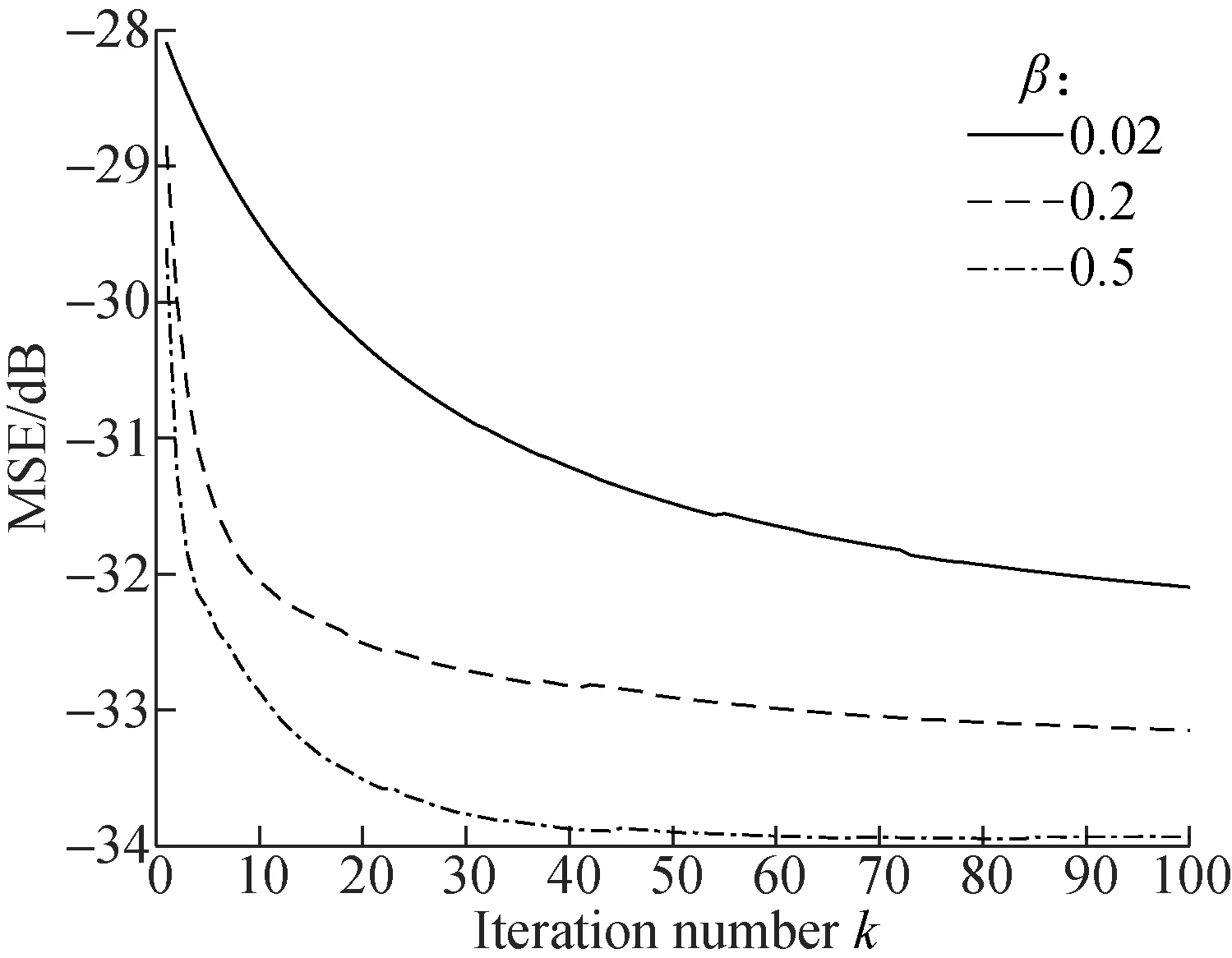
From Figs.12(a),(b),(c), it can be seen thatβcontrols the range of the iteration step. The largerβcan accelerate the convergence speed and converge after 30 to 40 iterations. The largerαcan also speed up the convergence speed, and the largerγcan also speed up the convergence speed. Therefore, the parameters of the adaptive filtering areα=5,β=0.2,γ=5.

(a)

(b)

Fig.11 Spectrum comparison. (a) Spectrum of original signal;(b) Spectrum of adaptive filtering signal

(b)

(d)

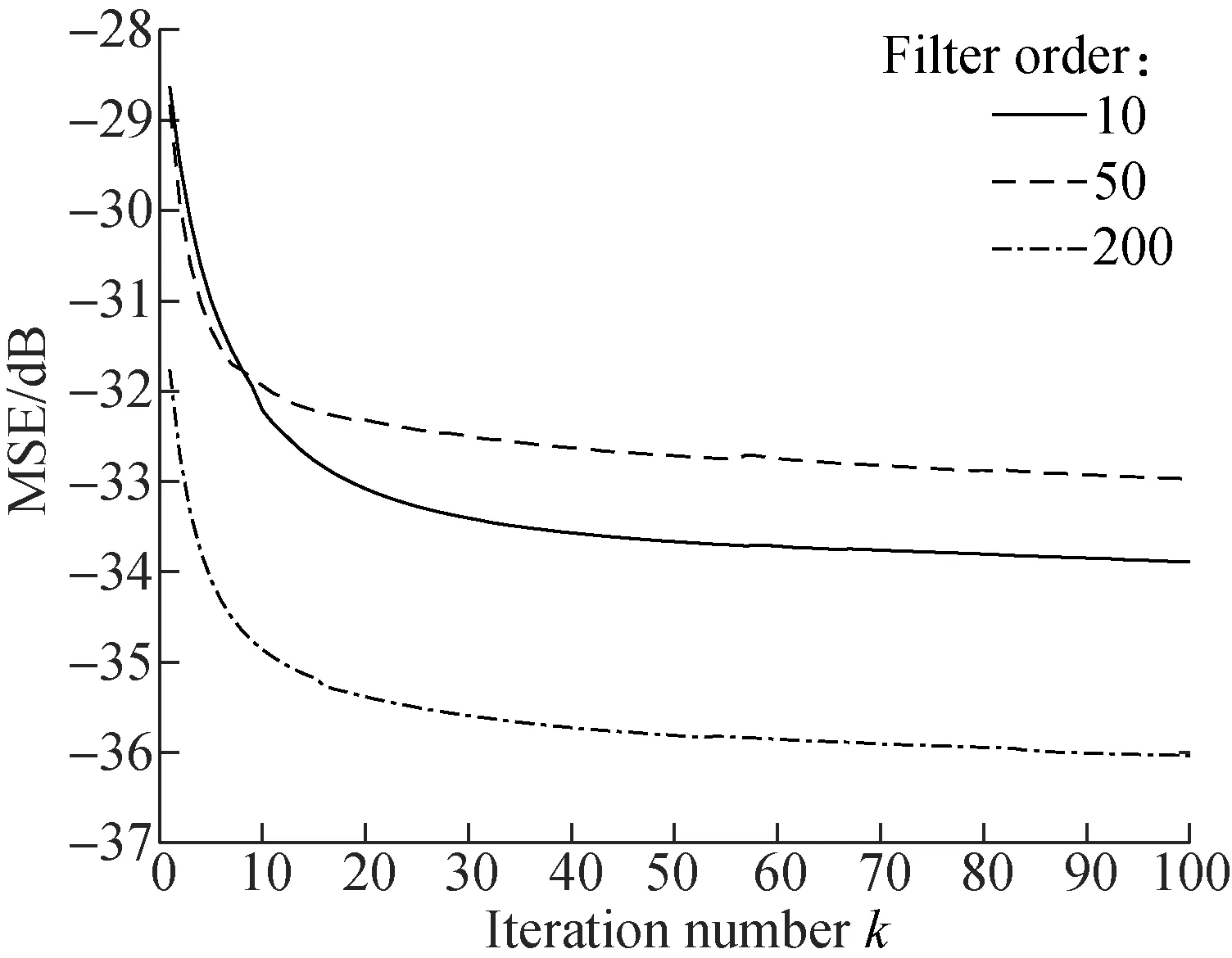
The filter order is also important in the adaptive filter. The filter order is set to be 10, 50, 200, and the results are shown in Figs.12(d). We can see that the larger filter order can accelerate the convergence speed and reduce the steady-state error.

3.3.2 Comparison with the existing algorithms

In order to find the superiority of the algorithm in this paper, the MSE of these algorithms are compared in the following figures. The parameters are set to beα=5,β=0.2,γ=3 andα=5,β=0.2,γ=5.

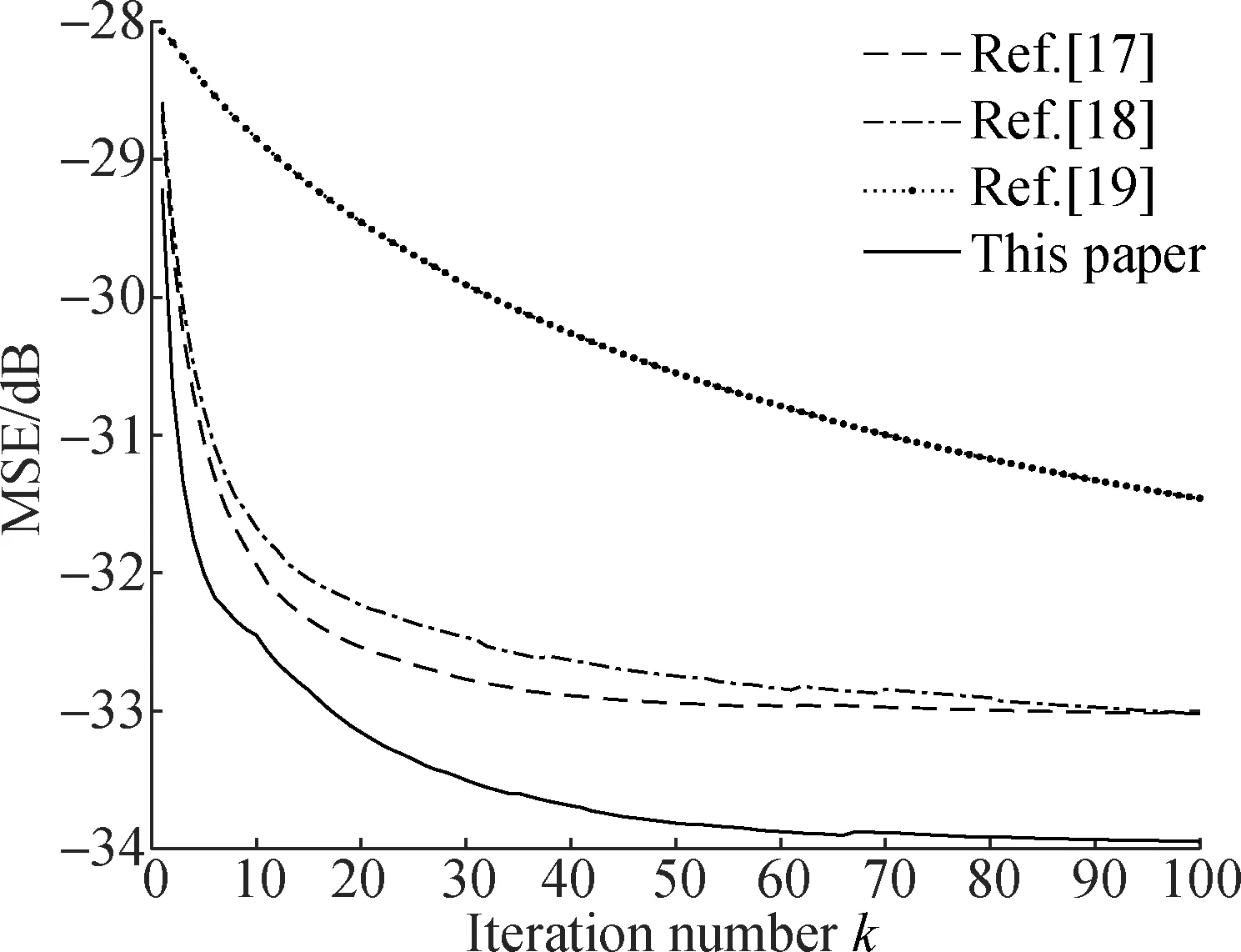
It can be seen from Fig.13 that in the case ofγ=3 andγ=5, the convergence speed of this algorithm is higher than those in other literature, and the steady-state error is relatively small. Therefore, it also illustrates the superiority of the algorithm in dealing with the contradiction between the convergence speed and the steady-state error which the traditional adaptive filter needs to solve, and also further explains the advantages of the algorithm, the feasibility and convenience of adaptive filtering technology in the field of acoustic emission.

Meanwhile, the spectrum of each algorithm after adaptive filtering is analyzed. The results are shown in Fig.14.

According to the experimental analysis,we can see that the peak spectrum of acoustic emission waveform is about 80 to 100 kHz. This algorithm has an obvious effect in reducing the high frequency noise signal(mainly mechanical vibration and environment noise), and it has the same performance as the existing algorithm. It is easy to see from Tab.1 that the SNR of the improved algorithm is relatively greater than others. At the same time, this algorithm weakens the peak spectrum of the main peak, and lays a foundation for the acoustic emission source positioning technology based on the waveform analysis.

(a)

(b)

(a)

(b)

(d)

Fig.14 Comparison in the spectrum of each algorithm. (a) The algorithm in Ref.[17]; (b) The algorithm in Ref.[18]; (c) The algorithm in Ref.[19]; (d) The algorithm of this paper>

4 Conclusions

1) An improved variable iteration step LMS adaptive filtering algorithm is proposed,which includes three parametersα,β,γand combinese(k) withe(k-1) in order to cope with error mutation. This algorithm improves the convergence speed and reduces the steady-state error.It has an obvious advantage over other existing algorithms.

2) In view of the special attenuation characteristics of the burst AE signal,adaptive filtering is applied to acoustic emission signal processing. A new method of constructing expectation function is proposed for acoustic emission signals, which is suitable for acoustic emission signals.

3) It is found that the improved algorithm also has a certain filtering effect in the frequency domain, which reduces the high frequency noise signal and makes the main frequency bands more prominent, and it has achieved a good filtering effect. It has a good application prospect in the field of AE signal processing especially in the source positioning of AE signals.