利用结构等效转换的空间可展机构装配误差建模与灵敏度分析

2019-04-04余德文赵强强陈飞飞郭俊康洪军

西安交通大学学报 2019年4期

余德文,赵强强,陈飞飞,郭俊康,洪军

(1.西安交通大学现代设计及转子轴承系统教育部重点实验室,710049,西安;2.上海宇航系统工程研究所,201109,上海)

由于运载火箭容积限制以及航天领域对空间天线性能要求的提高,大口径、高精度的空间可展机构一直是空间技术的研究热点。对于卫星天线来说,装配精度很大程度上决定着工作性能。在实际工程中,由于受到杆件加工误差、铰链装配误差的影响,空间可展机构装配精度往往达不到设计要求,为此工程人员经常在地面装配过程中对其支撑杆件进行尺寸调整。然而,由于不清楚误差源与装配精度之间的关系,航天企业目前采用测量、调整、测量的纯经验盲调模式。因此,从提高装配精度和实现定量装调的角度出发,一套行之有效的装配精度分析方法,对于保障空间可展机构装配质量和提高卫星天线服役性能显得尤为重要。

作为空间可展机构的典型代表,星载SAR天线空间可展机构备受学者关注。早期关于该类空间可展机构的研究主要集中在构型优化设计[1-5]和运动机理分析[6-11]上。继Campbell等发明可展支撑桁架结构[12]后,又经设计人员的不断改进[13-15],星载SAR天线空间展开机构已成功应用于美国SEASAT卫星[16]、欧空局ERS系列卫星[17]、加拿大RADARSAT系列卫星[18]、日本ALOS卫星[19]以及我国高分三号卫星[20]。

随着运动控制趋于成熟,该类可展机构的拓扑结构也逐渐定型,具有杆件与环约束多、环约束互相耦合等特点,给几何精度分析带来了极大困难,目前只有少数学者进行了相关探索。Hedgepeth提出以天线平面节点偏差均方根为评价指标进行型面精度分析[21];Greene建立了一种基于有限元分析的评估杆件单元长度不确定性对天线性能影响的方法[22];Mobrem进一步总结出分析空间可展机构杆长对天线性能影响的蒙特卡罗法、逆频率平方法、直接法与正则模法[23];受此启发,吴建云等利用蒙特卡洛法,研究了可展机构中铰链锁定位置偏差对展开精度的影响[24]。

上述精度分析方法是建立在关键设计参数随机分布的假设之上,结果无法指导具体产品的装调[21-24]。另外,由于星载SAR天线空间可展机构在理想情况下,构型关于展开方向与天线板垂线方向所构成的平面对称,因此一些研究者在分析其几何精度时按平面连杆机构简化处理。例如,文献[25-26]构建了单杆件固定、双杆件连接和多余杆件连接3种装配单元的误差模型,进而提出了多环闭链可展机构的精度预测算法,此模型对三维构型装配误差分析具有借鉴意义。文献[27]从几何误差角度求解了极恶劣工况下的指向误差。此外,张武翔等以结构势能最小为目标函数,建立了空间可展机构尺寸调整的数学模型[28],然而定义的综合调整量没有真实的物理含义,并且去掉了可展机构中的部分支撑杆件,减少了实际存在的环约束,因此工程应用具有较大局限性。

本文提出了一种空间可展机构装配误差建模和灵敏度分析方法。首先,通过空间可展机构的等效转换将其分为两部分,基于闭环矢量与虚位移法,分别建立这两部分结构的装配误差模型,经线性叠加后,全面表征出天线板位姿误差与误差源的函数关系,实现整个空间可展机构的几何精度预测。在此基础上,运用偏微分法分析装配精度受误差源的影响情况,从而识别出关键误差源,并通过具体数值算例验证所提方法的有效性。

1 问题描述

图1给出了星载SAR天线空间可展机构的展开构型,主要由天线内板、天线外板、支撑杆件、90°锁定铰链和180°锁定铰链组成。天线内板通过两个90°锁定铰链与星体连接,天线外板通过两个180°锁定铰链与天线内板连接,天线内外板依靠支撑杆件增强与星体的连接刚度。可以看出,空间可展机构实质上是一个超静定过约束机构。

图1 星载SAR天线空间可展机构

在实际装配过程中,空间可展机构调不准的顽疾至今仍未根除。因此,本文所需解决的问题是:如何从几何角度出发,构建空间可展机构装配精度与误差源的函数关系,并找出影响装配精度的关键杆件,以实现空间可展机构的装配误差预测和精准定量装调。

2 装配误差建模

2.1 结构等效转换

如前文所述,空间可展机构的展开构型属于典型超静定结构。在不考虑变形且不影响装配精度的前提下,必须进行结构等效转换以消除过约束。为此,将空间可展机构分为图2所示的两部分。第一部分由外撑杆、中撑杆、内撑杆及天线面板组成的不含星体连接杆的支撑结构;第二部分由星体连接杆与虚拟杆件(连接撑杆交汇中心O与90°锁定铰链几何对称中心B的假想杆件,其简要表征不含星体连接杆的支撑结构)组成的双杆件连接结构。

上述转换的理由如下:由于SAR天线内外板间180°锁定铰链的间隙十分微小,并且铰链锁定后的结构刚度较大,因此两板原有的平面度在整个装调过程中保持不变,从而可把内外板视为一块整板。不同于180°锁定铰链的是,连接星体与天线内板的90°锁定铰链间隙相对较大,容许天线面板一定范围内的装配误差。综上所述,将空间可展机构分成两部分结构具有合理性。

图2 空间可展机构等效转换模型

2.2 不含星体连接杆的支撑结构误差建模

将支撑结构第一部分视作6-SPS(S-球铰副,P-移动副)结构。一方面,杆长调整(加减垫片)的过程类似于移动副的直线运动,实质均是沿特定方向的特征尺寸发生改变;另一方面,由于天线面板位姿变化空间十分微小,且铰链转动副间存在径向间隙,因此球铰副代替转动副为工程所接受。

如图3所示,在6杆交汇中心的位置O建立局部坐标系O1-x1y1z1,x1轴正向沿天线面板长度方向并远离星体,y1轴正向沿天线面板宽度方向且竖直向下,z1轴正向由右手法则确定。此外,在天线面板的几何中心A建立局部坐标系O2-x2y2z2,该坐标系与坐标系O1-x1y1z1平行。

图3 不含星体连接杆的支撑结构

在第i个封闭环O-A-Ai-O(i=1,2,3,4,5,6)中,满足闭环矢量方程[29]

liui=r+Rai

(1)

式中:ui为由O指向Ai的单位矢量;li为杆件OAi名义长度;r为坐标系O1-x1y1z1下由O指向A的矢量;R为坐标系O2-x2y2z2到坐标系O1-x1y1z1的齐次变换矩阵;ai是Ai在O2-x2y2z2坐标系下的坐标。对式(1)两边全微分,有

dliui+lidui=dr+dRai+Rdai

(2)

(3)

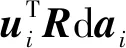
(4)

(5)

在式(3)中,与名义杆长相比,杆长误差均可视作无穷小量,即dli=Δli,dr=Δr,dai=Δai。接着,把式(4)带入式(3)中,整理后可得

(6)

式(6)的矩阵表达形式如下

(7)

6个封闭环O-A-Ai-O均满足等式(7),将其完全组合有

ΔL=JvΔV+JbΔB

(8)

式中:ΔL=[Δl1,Δl2,Δl3,Δl4,Δl5,Δl6]T,分别对应6杆的长度误差;ΔB=[Δa1,Δa2,Δa3,Δa4,Δa5,Δa6]T,分别为6个铰链的安装位置误差,有Δai=[Δxi,Δyi,Δzi];ΔV=[Δr,Δθ]T,Δr、Δθ分别为天线板相对于坐标系O1-x1y1z1的位置误差、姿态误差;Jv、Jb为ΔV、ΔB相应的系数矩阵,其具体表达式如下

(9)

由式(8)可得到不含星体连接杆的支撑结构装配误差的正解方程

(10)

至此,式(10)表达了天线面板位姿误差与6个杆长误差、6个铰链安装位置误差的函数关系,而该位姿误差是在坐标系O1-x1y1z1下衡量的。只要进一步得到坐标系O1-x1y1z1与全局坐标系的相对位姿关系,便能在全局坐标系下求解出天线面板的装配误差。

2.3 含星体连接杆的支撑结构误差建模

如图4所示,全局坐标系Og-xyz的原点为两个90°锁定铰链理论安装位置的几何对称中心B,x轴正向为沿天线面板长度方向并远离星体,y轴正向为沿天线面板宽度方向且竖直向下,z轴正向根据右手法则确定。在全局坐标系Og-xyz中,局部坐标系O1-x1y1z1坐标原点O(O1)受星体连接杆影响,名义位置与实际位置之间存在装配误差。因此,下面将构建双杆件连接装配误差模型,并确定O点位置误差对空间可展机构几何装配精度的影响。

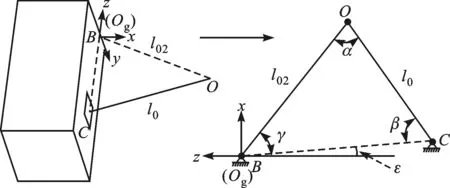
图4 双杆件连接结构及其平面表征

由于全局坐标系Og-xyz和局部坐标系O1-x1y1z1完全平行,星体连接杆CO和虚拟杆BO都在xz平面,因而投影至平面表征出如图4所示的双杆件连接结构。在图4情况下,O点的装配位置误差由杆件BO、CO的杆长误差与铰链连接处B、C的位置误差造成。因此,O点位置误差可以表示为

ΔO=μ1Δl+μ2ΔB+μ3ΔC

(11)

式中:ΔO表示O点位置误差;Δl=[Δl02,Δl0]T,Δl02、Δl0分别为BO、CO的杆长误差;ΔB=[ΔzB,ΔxB]T,ΔzB、ΔxB分别表示B在全局坐标系下沿z轴、x轴的位置误差;与ΔB类似,ΔC=[ΔzC,ΔxC]T表示铰链C处的位置误差;μ1、μ2、μ3分别为相应误差系数矩阵,且定义如下

(12)

图5 系数矩阵部分表达式计算原理图

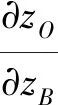
(13)

通过构造与图5相似的结构可以求解系数矩阵的其它比值,由此得到的3个系数矩阵具体为

(14a)

μ2=

(14b)

μ3=

(14c)

式中:α、β、γ为名义尺寸下各铰接点所组成三角形的内角;ε为BC连线与z轴负方向的夹角。

需要特别指出的是,利用式(11)求解O点的装配位置误差时,两个90°锁定铰链理论安装位置的几何对称中心B点作为基准点,其装配误差为0。另外,虚拟杆件BO在理想条件下的矢量表达式为

l02=r+l01

(15)

(16)

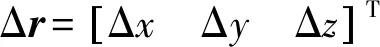
Δl02=((rx+Δx-l01)2+(ry+Δy-δzl01)2+

(17)

将式(17)(14)带入式(11),可计算出O点的装配误差。注意到ΔO只在xz平面,不影响绕x方向和z方向的转动偏差,而所引起空间可展机构绕y轴的转动偏差为

ξy=‖ΔO‖/l02

(18)

利用线性叠加,综合式(10)(18),得到考虑所有杆长误差与铰链安装位置误差的空间可展机构几何装配精度模型

(19)

式中:ΔP=[Tx,Ty,Tz,Rx,Ry,Rz]T,为全局坐标系下空间可展机构的位姿误差。

3 灵敏度分析

由于在实际装调过程中,可展机构绕y轴的偏摆误差通常更难以满足设计要求。因此,下面着重分析各误差因素对可展机构y轴姿态误差的影响,而其余的灵敏度分析可据此类推。

3.1 杆长误差影响系数

基于空间可展机构几何装配精度模型,由式(19)的位姿误差与误差源的函数关系,可分离出到可展机构y轴偏摆误差与各项误差的关系,即

Ry=δy+ξy

(20)

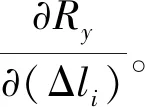
(21)

(22)

式中:J1i,…,J6i为误差传递矩阵J各行第i列的值。

另外,从式(10)可知,ΔV=[Δx,Δy,Δz,δx,δy,δz]T均是杆长误差Δli(i=1,2,3,4,5,6)的函数。从式(17)可以看出Δl02是ΔV的函数。以此推出,Δl02也是Δli(i=1,2,3,4,5,6)的函数。于是,式(17)两边对杆长误差Δli求偏导有

(23)

(24a)

i=1,2,3,4,5,6

(24b)

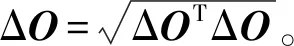
令

(25)

综合式(23)(24)(25),各项杆长误差对天线面板y轴偏摆误差影响的灵敏度表达式如下

(26)

3.2 铰链安装位置误差影响系数

类似地,按照推导杆长误差影响系数的思路,利用式(11)和式(20),可以得出C处铰链安装位置误差对天线面板绕y轴偏摆误差影响的灵敏度表达式如下

(27a)

(27b)

除C处铰链外,天线面板上Aj(j=1,2,3,4,5,6)处铰链同样存在安装位置误差。为简化表达,以Δajk(j=1,2,3,4,5,6;k=x,y,z)表示Aj处铰链在k方向的安装位置误差。由式(10)(17)可知,Δl02也是Δajk的函数,进而对表达式(17)进行相应铰链安装位置误差取偏微分,可以得到

(28)

在此基础上,构建映射关系:当k=x时,n=1;当k=y时,n=2;当k=z时,n=3。令m=3(j+1)+n(j=1,2,3,4,5,6;n=1,2,3),利用式(20),推导出天线面板处铰链安装位置误差对天线面板绕y轴偏摆误差影响的灵敏度表达式如下

(q3J5m-q4J6m+q5J1m+q6J2m+q7J3m)

(29)

式中:J1m,…,J6m为误差传递矩阵J各行第m列的值。

至此,式(27)和式(29)完全表达了各铰链安装位置误差对天线面板y轴偏摆误差影响的灵敏度。

4 案例分析

某星载SAR天线空间可展机构的具体尺寸如表1所示,天线阵面长为2.22 m,宽为1.65 m。为保障卫星正常服役所需的电性能,在地面装配中,特别要求天线面板俯仰角与方位角均优于0.020°,该精度指标对应本模型中的y轴偏角(Ry)与x轴偏角(Rx)。

该机构属于精密杆系机构,杆件加工精度等级取11级,中撑杆的半公差带宽为0.66 mm,其余杆件的半公差带宽均为1.10 mm。实际装配过程中,铰链安装位置误差在3个坐标方向上均不超过0.20 mm。在上述相应误差范围内,给定5组如表2所示的杆长误差和铰链安装位置误差。运用MATLAB编写几何装配精度分析程序,根据式(19)计算出装配误差,结果详见表3。

表2 杆长与铰链安装位置误差值

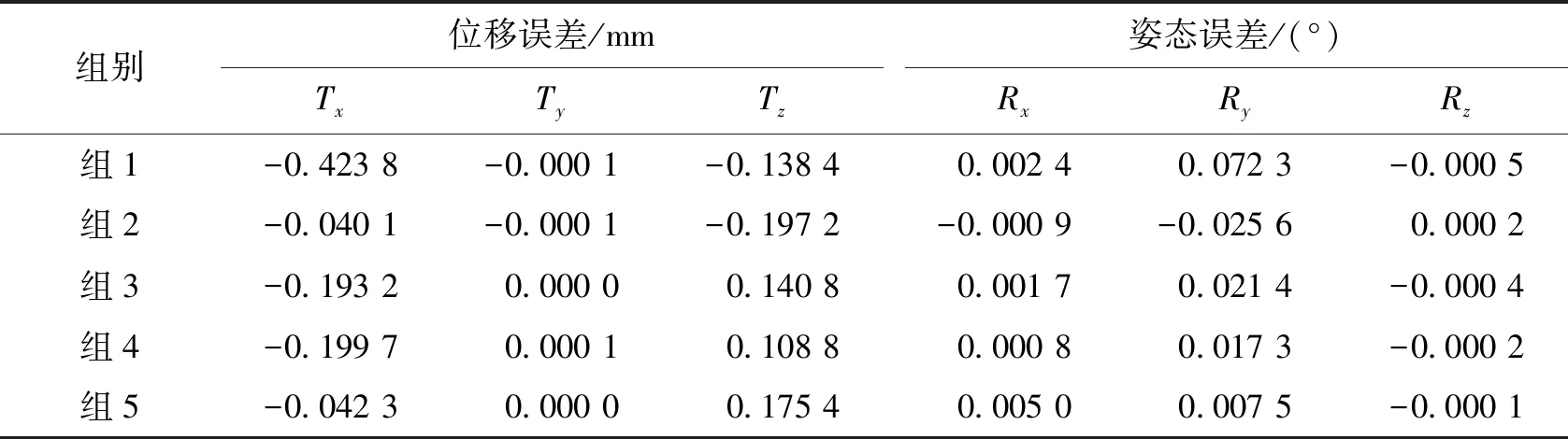
表3 空间可展机构位姿误差

从表2与表3可以看出,在误差组1、2、3作用下,天线面板绕y轴方向的偏摆误差(Ry)均大于0.02°。这说明,即使杆长误差满足设计要求,铰链安装符合工艺要求,依旧无法完全保证天线面板的指向精度。为进一步反映杆件动态调整过程,在误差组1的基础上,只调整支撑杆件长度而保持铰链安装位置误差不变,依据误差组1、3、5的计算结果,注意到Rx始终在允许范围内,而Ry从0.072 3°到0.021 4°再到0.007 5°,因此逐渐满足装配精度要求。较误差组3而言,误差组4全面调整了安装位置误差,误差组5仅微调内撑杆Δl5与星体杆Δl0的尺寸,两种方法均获得了理想的装配精度。由此可见,在满足杆件加工精度和铰链安装精度条件下,尽管调整铰链安装位置也能限制天线面板的装配误差,但考虑到装调时间和装调难度,调整杆长不失为更合理的选择。另外,从表3还可以看出,上述误差作用下的天线面板沿y轴方向的位移偏差(Ty)几乎为0,且绕z轴方向偏摆误差(Rz)的绝对值不超过0.001°,这符合平面天线空间展开机构完全展开状态下的结构特征。

正如上文分析结果,在实际装调过程中,工厂也只选择对杆长加减垫片进行空间可展机构装配精度的调整。为进一步识别出关键杆件以降低装配难度,依据式(26),计算出各杆长误差对天线面板绕y轴偏摆误差影响的灵敏度值,详见表4。