电动汽车混合储能系统的自适应协同控制
2019-04-04续丹周佳辉王斌毛景禄汪建林
续丹,周佳辉,王斌,毛景禄,汪建林
(西安交通大学机械工程学院,710049,西安)
在环境污染和能源危机的背景下,电动汽车受到广泛的关注与重视,成为当下研究的热点[1-3]。然而,电池作为电动汽车传统储能和供能装置,其技术尚不完善,存在功率密度低、循环寿命短等问题。由于超级电容具有功率密度高、循环寿命长等优点[4-6],因此电池与超级电容组合的混合储能系统应运而生,该系统兼具高能量密度和高功率密度的优点,既能够保证电动汽车在各种工况下的功率需求,又能有效延长电池的使用寿命[7-9]。
在混合储能系统中,通常采用直流变换器实现电池和超级电容之间的功率分配。直流变换器是一种典型的非线性、时变系统,对其控制的研究吸引了众多研究者。传统的PI控制等方法只能使系统工作在某个具体的点附近,因而不适用于电动汽车多工况、负载频繁变化的情况。滑模控制已经被成功应用于直流变换器的控制中,具有降阶、去耦合以及对参数变化不敏感等优点,但其控制器带宽过高、开关切换频率变化导致其存在颤振问题,不易数字化实现[10-11],而协同控制不仅具有与滑模控制相同的降阶、去耦合优点,又因其开关切换频率固定、不存在颤振问题而非常便于数字化实现[12-14]。
协同控制采用解析的方法,充分利用系统数学模型实现非线性系统的控制[12-15],可以保证控制的精准性。合理设计协同控制器,能够保证系统的闭环稳定性、鲁棒性以及良好的动态响应特性,因此协同控制非常适用于电动汽车混合储能系统的控制与功率分配。然而,协同控制需要知道完整的系统信息,但在实际应用中,负载信息往往是未知的,且电池和超级电容均存在动态变化的内阻,这都是协同控制器设计时需要考虑的因素。
为了提高电池-超级电容混合储能系统的稳定性和控制的准确性,以及保证功率分配的有效实施,本文在协同控制的基础上设计了一种自适应协同控制策略。首先,在系统理想状态空间平均模型的基础上设计了协同控制器,并验证了其稳定性;其次,考虑各电源内阻定义了自适应观测函数,并基于Lyapunov函数设计自适应控制律,对负载及输入电压进行估计;然后,选取了合理的协同控制宏变量,并由此推导出自适应协同控制的占空比函数;最后,通过仿真验证了所提出的自适应协同控制策略在混合储能系统电流跟踪控制中的效果。
1 模型建立
本文采用半主动结构的电池-超级电容混合储能系统,Vbattery为电池输出电压;L、C、R分别为电感、电容和负载电阻,系统结构如图1所示。电池组电压低于超级电容电压,经过一个直流变换器升压输出,超级电容直接输出。
状态空间平均法是直流变换器瞬态建模分析的常用方法之一。假设升压变换器输入端电池电压无波动、忽略超级电容影响,当SW导通时,有
(1)
式中:x1为电感电流;x2为输出电压。当SW关断时,有
(2)
由式(1)和式(2)可以得出系统的理想状态空间平均模型为
(3)
式中:d为占空比。
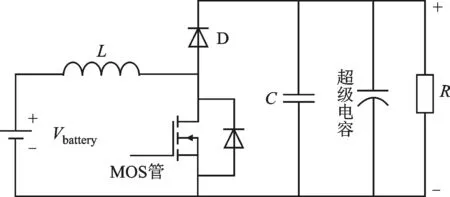
图1 半主动电池-超级电容混合储能系统
2 协同控制
协同控制是以自组织思想为基础演变而来的非线性系统控制方法。该方法利用系统状态空间模型,引入宏变量定义状态变量之间的关系,迫使系统从任意初始点运动至一不变的流形,并最终沿着这一流形达到稳态[12-14]。
2.1 协同控制器设计
首先,定义宏变量ψ,表达式为
ψ(t)=ψ(x,t)
(4)
控制器通过控制这一宏变量ψ迫使系统工作在流形,即ψ=0。ψ=0这一条件也使得系统的阶次降低一次。通过定义ψ,设计者可以根据需求引入不同的控制律以提升控制性能。
式(5)定义了宏变量ψ在工作平面内的动态运动规律,即宏变量ψ需满足

(5)
式中:T为时间常数,理论上可以任意小。T决定系统收敛于流形的速度,T越小收敛速度越快,稳态误差和系统噪声也越小[16]。一般情况下系统在t=3T时系统即可达到目标流形。
通过求解式(5)可得出控制变量的表达式,在本文中即为占空比d的表达式。
在直流变换器的控制中,滑模控制在滑模面附近采用bang-bang控制会导致开关切换频率无穷大,采用滞环控制虽然能够有效降低开关切换频率,但开关切换频率是变化的,而协同控制通过生成占空比d使系统满足式(5),通过产生PWM信号进行控制,开关切换频率固定,不会引起颤振问题。因此,与滑模控制相比,协同控制具有以下优点[12-13,16-18]:①开关切换频率固定;②易于数字化实现;③偏离目标流形时的动态响应由T决定而非完全依赖于系统原有属性。
协同控制中,最简单的宏变量ψ可定义为系统状态变量的线性组合,即
ψ=k1(x1-x1ref)+k2(x2-x2ref)
(6)
式中:x1ref为参考电流;x2ref为参考电压。当系统工作在流形ψ=0时,状态变量之间为线性关系,即系统的阶次减小一次。系统阶次的减小,可以有效抑制超调的产生。
联立式(3)~式(6),得出占空比
(7)
式(7)为协同控制器的控制律,用于控制本文中的直流变换器。该控制律控制系统状态变量x1、x2收敛于流形ψ=0,并沿着该流形向稳态工作点运动,最终到达稳态工作点x1=x1ref,x2=x2ref。
式(7)表明,由于协同控制使用了系统完整的数学模型,其控制律的形式相对复杂、计算量增大,但利用现有的处理器(如DSP等)可有效解决上述问题。此外,使用完整的数学模型会导致系统对参数变化的敏感性增大,这一问题可通过合理定义宏变量ψ解决。
2.2 稳定性证明
选取Lyapunov函数为
V=0.5ψ2
(8)
进一步求导得
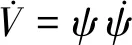
(9)
(10)
根据Lyapunov稳定性原理,可知系统是渐近稳定的。
3 自适应协同控制
由式(7)可知,协同控制律中存在-k2x2/RC项,即控制律的实现需要知道准确的负载信息,这在实际应用中显然是难以实现的。虽然根据欧姆定律R=U/I可以计算负载的大小,但是瞬态时负载端电压和电流测量值滞后,导致此时误差较大,严重影响系统的瞬态响应性能。另外,式(3)为理想状态下的状态空间平均模型,为实现精确控制,需要考虑电池内阻带来的输入电压波动和超级电容等效内阻的影响,并且电池和超级电容的内阻又是动态变化的[4,19-20]。针对以上问题,本文结合自适应控制理论对协同控制进行改进,设计了一种自适应协同控制策略:基于Lyapunov函数设计自适应状态观测器对负载及输入电压进行估计,以克服系统参数变化引起的电压和电流波动。


图2 半主动电池-超级电容混合储能系统等效模型
系统等效数学模型可以写成
(11)
根据以上模型,可以将输入电压和等效负载作为估计量,建立观测函数
(12)
(13)
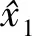

(14)
(15)
建立Lyapunov函数
(16)
(17)
式中:ξ1和ξ2为正常数
(18)
(19)

选取协同控制宏变量为
(20)

根据式(5)和式(20),可得
(21)
式(21)即为本文所提出的自适应协同控制策略的占空比函数。
4 仿真验证
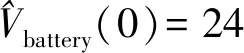
首先,为了验证本文自适应协同控制策略的有效性,分别将协同控制(负载由欧姆定律R=U/I计算得出,以下简称协同控制)、滑模控制与本文自适应协同控制策略得到的电池输出电流跟踪效果进行对比,3种策略均考虑各电源内阻。在电流控制时,电流误差的反馈起主要调节作用,因此需选取p1>p2,本文中取p1=9,p2=2。设置参考电流为10 A,负载为10 Ω,在t=0.02 s时并入另一个10 Ω负载,得到的电流跟踪效果和系统输出电压特性如图3和图4所示。
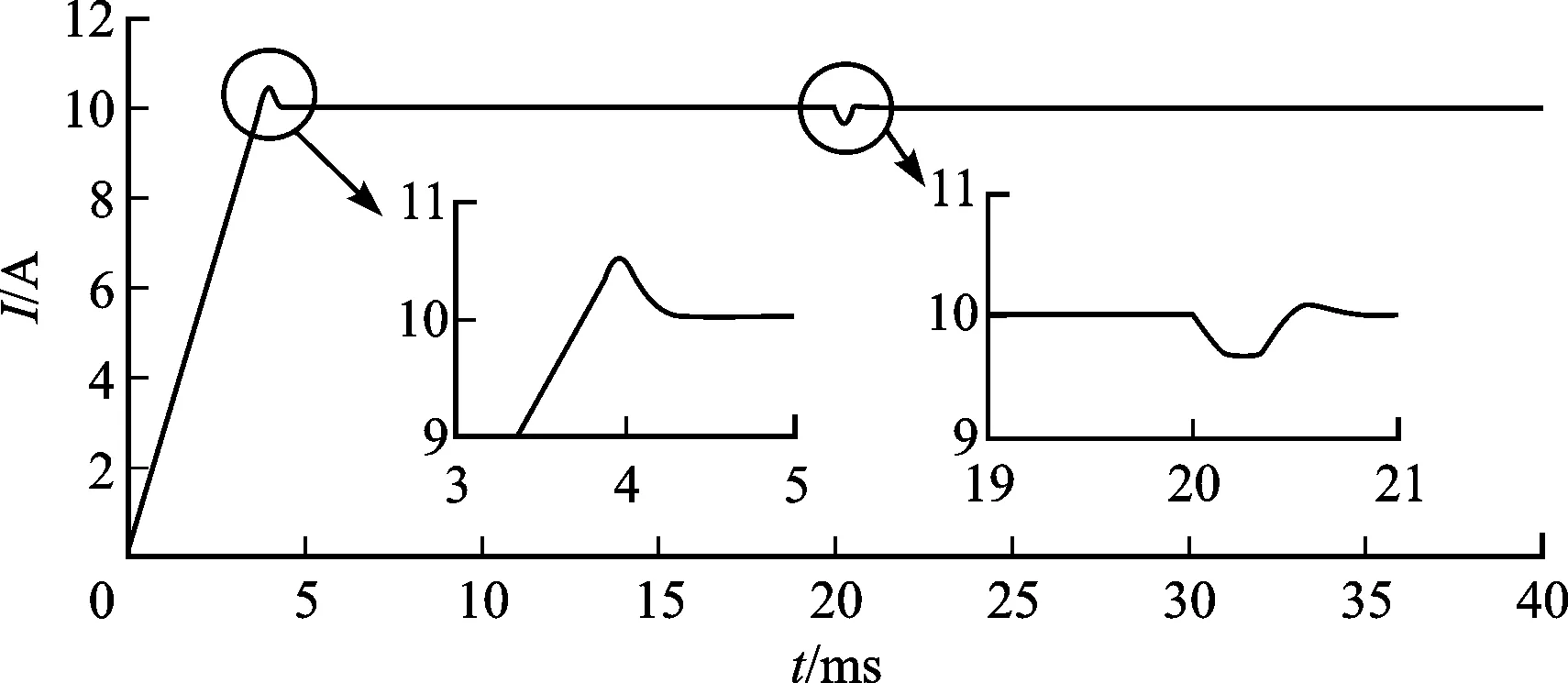
(a)协同控制

(b)滑模控制

(c)自适应协同控制图3 3种控制策略的电流跟踪控制效果对比
由图3可知:启动时,协同控制与滑模控制的响应时间基本相同,约为4.3 ms,且两者均存在明显的超调;自适应协同控制响应速度稍快,约为4 ms,且超调明显减小,仅为协同控制的40%、滑模控制的50%;负载波动时,协同控制与滑模控制的波动明显,响应时间约为8 ms;自适应协同控制响应速度快,约为3 ms,这是因为自适应协同控制有效减小了负载突变造成的电流波动。以上分析表明:协同控制与滑模控制的控制效果相近,这与文献[14]的结论相同;自适应协同控制响应速度快,系统稳定性和抗干扰能力更强。因此,自适应协同控制非常适用于混合储能系统中功率分配策略的实现。需要指出的是,由于采用自适应估计的方法,图3c中实际电流与参考电流之间的稳态误差大于图3a和3b,但不超过1%。
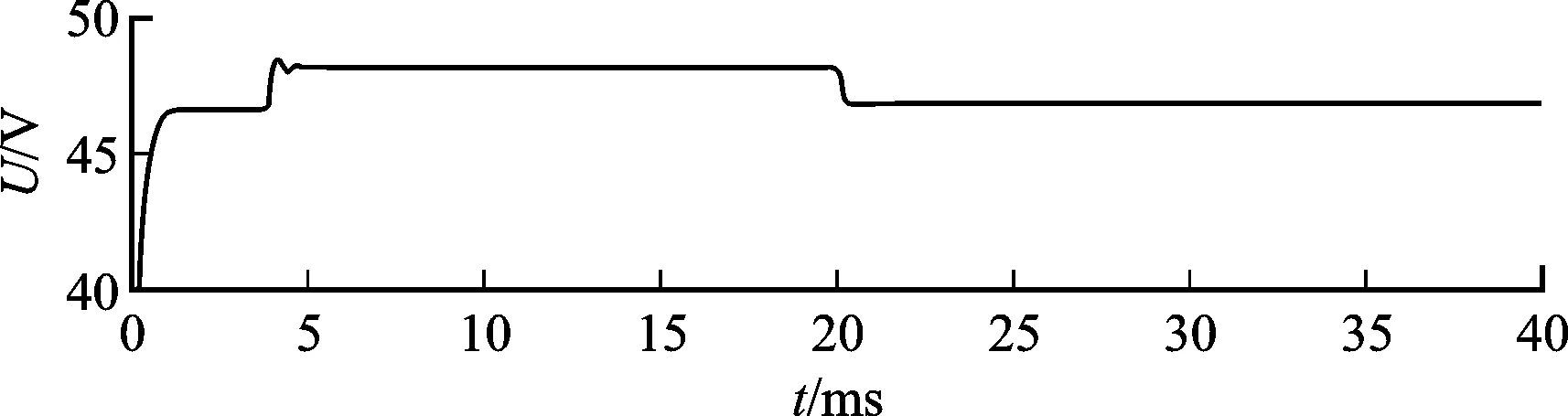
(a)协同控制
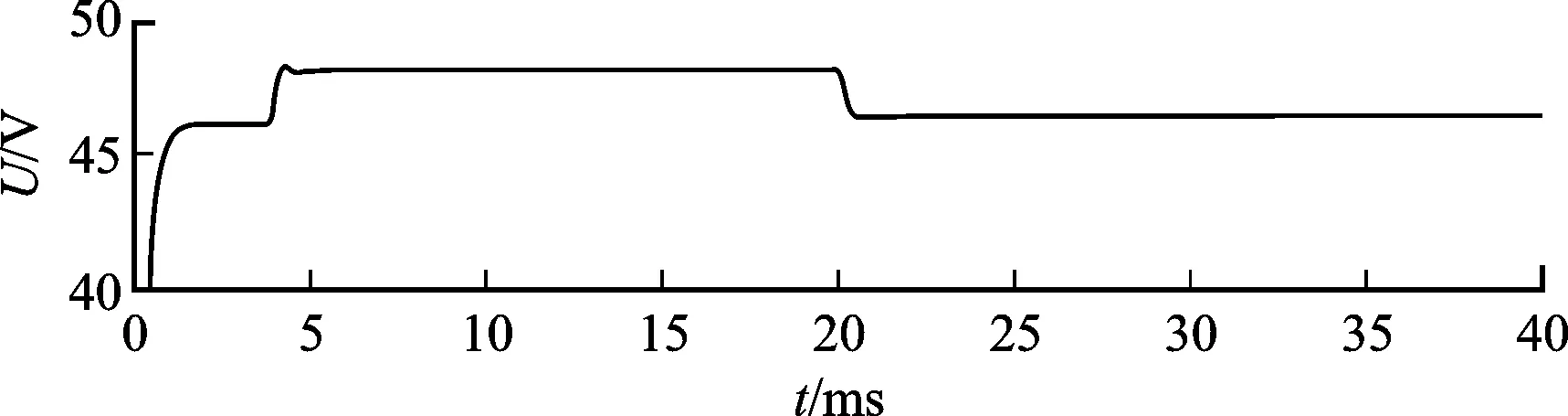
(b)滑模控制

(c)自适应控制图4 3种控制策略下系统的输出电压特性

为进一步验证本文提出的自适应协同控制在混合储能系统功率分配中的性能,以电池输出电流为控制量,设计了短时间内连续变化的参考电流模拟工况对其进行验证。实验中保持负载需求功率不变,控制电池跟随参考电流输出,剩余功率由超级电容补偿。结果如图5所示。
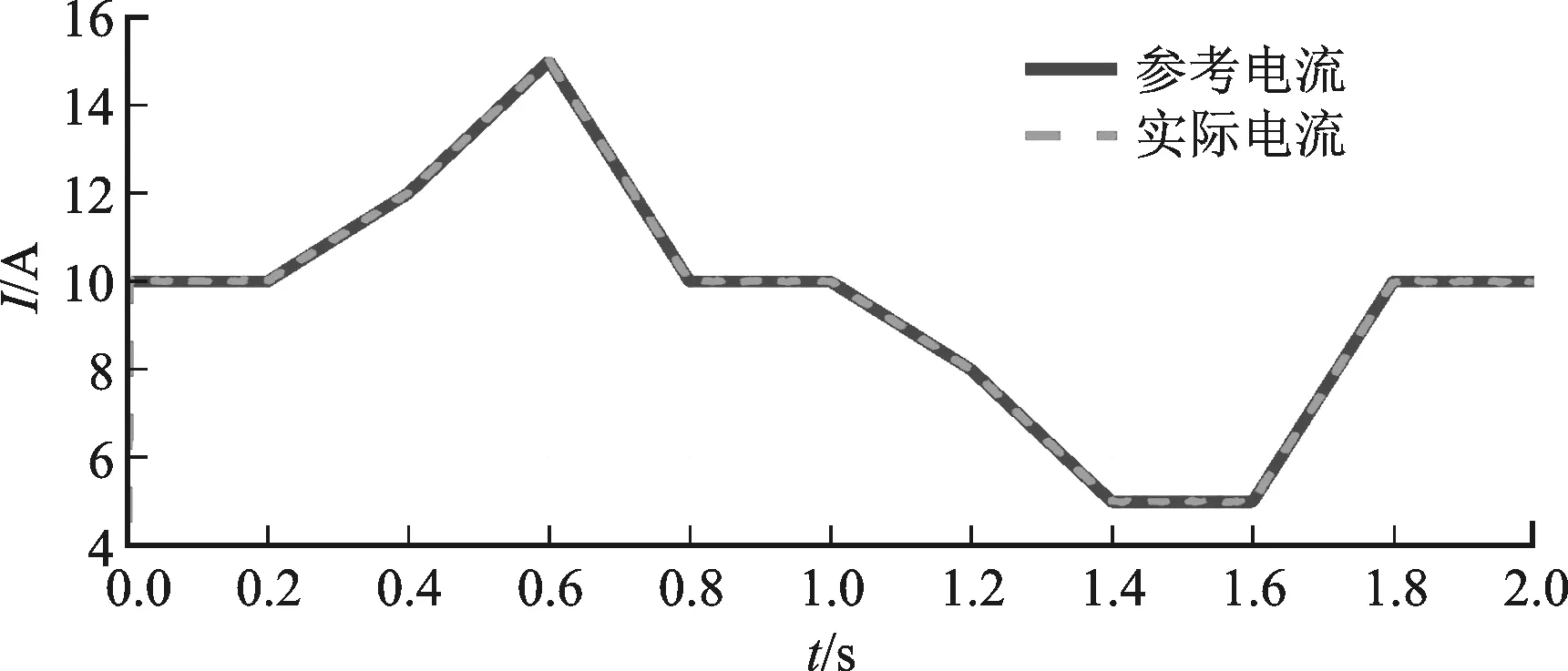
(a)电池参考电流与实际电流
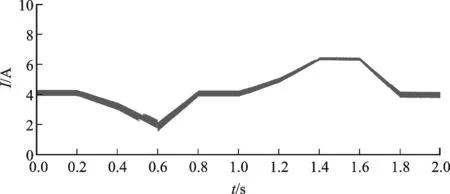
(b)超级电容输出电流图5 参考电流连续变化时的电流跟踪效果
由图5可知,在参考电流连续变化的情况下,电池实际输出电流能够迅速响应(响应时间约为4 ms),并能准确跟踪参考电流值变化(跟踪误差小于1%)。这一特性在混合储能系统的功率分配中非常适用,不仅能够有效保证功率分配策略的有效实施,还能保证电池输出的稳定性,充分发挥超级电容“削峰填谷”的作用。
5 结 论
电池-超级电容混合储能系统采用协同控制时,控制准确度较高且开关切换频率固定而不存在颤振问题。但是,协同控制需要知道准确的负载信息,在实际中由欧姆定律计算负载会降低系统瞬态响应性能;并且,实际应用中电池内阻带来的输入电压波动和超级电容等效电阻的影响也不可忽视。针对以上问题,为提高系统的稳定性和控制的准确性,本文提出了一种自适应协同控制策略。在直流变换器状态空间平均模型的基础上,考虑各电源内阻定义自适应观测函数,并基于Lyapunov函数设计自适应控制律,对负载及电源内阻进行估计;选取协同控制宏变量并由此推导出自适应协同控制的占空比函数,对混合储能系统进行电流跟踪控制。结果表明,自适应协同控制响应速度较快,约为4 ms,且没有明显的超调以及因负载变化造成的电流波动;电流跟踪控制时响应速度快且跟踪误差不超过1%;说明系统稳定性和抗干扰能力较强,控制准确性较好。因此,自适应协同控制能有效保证混合储能系统的稳定性和功率分配的准确性。
