利用打印条码的转子轴向位移径向监测方法
2019-04-04朱永生陈凯达闫柯曹鹏辉袁倩倩洪军
朱永生,陈凯达,闫柯,曹鹏辉,袁倩倩,洪军
(西安交通大学现代设计及转子轴承系统教育部重点实验室,710049,西安)
转子轴向位移是反映转子系统及机械设备运转状态的关键技术指标,是转子系统安全监测及系统特性研究中常用的监测量[1]。例如,汽轮机运行过程中的转子轴向位移是反映轴向推力的主要参数[2];精密机床通过实时监测电主轴高速切削时的轴向位移,可实现对主轴热伸长和位置变化的自动补偿,显著提高机床加工精度[3]。此外,轴向位移在转子系统控制中起关键作用,如电磁轴承中通过测量转子的轴向位移精确控制转子轴向位置,否则转子将无法平衡,甚至造成更加严重的后果[4]。在智能轴承技术中,转子轴向位移被用于反映轴承的载荷情况,进而开展寿命评估和状态控制[5]。因此,开展转子轴向位移监测方法的研究具有重要意义[5-8]。
常用的轴向位移测量方法是利用非接触式位移传感器直接测量轴端面或推力盘的轴向位移,但随着转子系统集成度的不断提高,转子的动力输出及测试装置都将集中于转子轴向,可供轴向位移传感器使用的测量空间不足,限制了传统轴向位移监测技术的应用。为此,国内外研究学者提出了通过径向布置传感器测量转子轴向位移的方法。根据所使用传感器类型,转子轴向位移的径向测量方法可以分为基于互感效应的测量方法、基于涡流效应的测量方法和基于霍尔效应的测量方法。
在基于互感效应的测量方法方面,主要通过在转子和定子径向上布置电感线圈,利用轴向位移引起线圈电感的变化来实现轴向位移的测量,但该方法所采用的传感器结构复杂,安装调试相对困难[9-11];Hawkins等利用互感原理实现了转子轴向位移的径向测量,主要优点是对于外界磁场的变化敏感程度低[12-13];Zong等研制了一种新型线性差动位移测量传感器,利用E型电感线圈与缠绕在转子上的电感线圈互感的原理实现轴向位移测量,由于测量线圈与转子径向距离影响线圈输出,转子径向振动会引起轴向位移测量误差[14]。
在基于涡流效应的测量方法方面,李红伟和边忠国提出了利用电涡流传感器从径向监测转子台阶位置进而获得轴向位移的方法[15-16],原理是转子台阶面的轴向位移改变传感器有效感应面积,从而使得电涡流传感器电压发生变化。该方法要求转子的运动不能超出传感器探头作用的台阶面范围。为了解决上述测量范围小的问题,文献[17-19]在转子回转表面加工锥面,当轴向产生位移时,利用锥面与传感器径向距离发生相应变化的原理实现对轴向位移的测量。上述方法均需要对轴系进行一定程度的改动,工程应用受限。
基于霍尔效应的测量方法主要在日本NSK公司应用,Koichiro为了测量NSK公司汽车轮毂轴承的预紧力,利用磁性编码盘和霍尔传感器,实现了径向测量转子轴向位移[20-22],测量原理为:利用两路霍尔传感器检测磁性编码盘,转子轴向位移会引起两路传感器输出信号产生时间延迟,通过时间延迟计算得到转子的轴向位移。该方法存在的问题是:需要根据转子的尺寸加工磁性编码盘,通用性不好;需要改造转子结构,磁性编码盘固定困难。
综上可知,目前转子轴向位移的径向测量方法的共同特点是,需要对转子系统进行改造或在轴端增加辅助测量装置,工程应用不便;传感器输出受径向振动、电磁干扰影响(如电涡流传感器)大,引起轴向位移测量误差。针对上述问题,本文提出了基于打印条码和激光光纤传感器的轴向位移的径向监测方法,用于解决工程实际中轴向空间受限情况下轴向位移测量的难题,为轴向位移监测和测量提供了一种新的解决思路。
1 基于时间延迟的位移测量原理
本文使用的条码设计为V型,由高精度激光打印机在打印纸上打印得到,如图1所示。

图1 时间延迟法测量条码
测量条码由测量区和接口区两部分组成。测量区内包含n个距离为w的白色V形条码,夹角为2β,条码宽度为w0。接口区宽度大于2w0,用于产生键相信号。
选用两个激光光纤型色标传感器用于V型条码边缘检测。两个传感器相互平行、同时垂直并通过转子中心线安装,如图2所示。
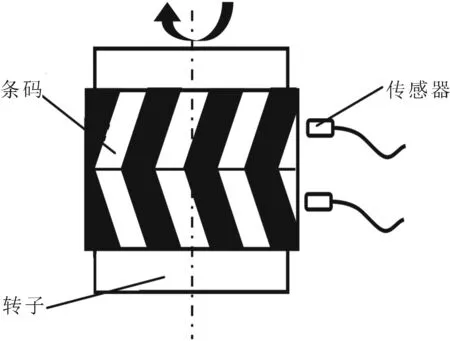
图2 时间延迟法传感器布局示意图
采用时间延迟法对轴向位移进行测量,原理如下:假设两个激光光纤色标传感器间隔为S,转子产生轴向位移Δz前后,传感器与转子的相对位置如图3所示。

图3 位移前后传感器与转子相对位置示意图
两路传感器在条码表面的扫描轨迹如图4a所示,当转子轴向位移Δz时,新轨迹与原轨迹距离差也为Δz。转子产生轴向位移前后,两个传感器对应输出信号如图4b所示。传感器输出信号为一系列脉冲信号,当传感器扫过白色区域输出高电平信号,否则输出低电平信号。轴向位移发生前,令传感器a与传感器b输出信号的时间延迟为t,当轴向位移为Δz时,两路传感器输出信号延迟变为t′。由几何关系可得,信号的时间延迟与局部周期满足
(1)
(2)
式中:T为轴向位移前的局部周期;T′为轴向位移后的局部周期;β为V字型条码夹角的一半。

(a)传感器在条码上的扫描轨迹
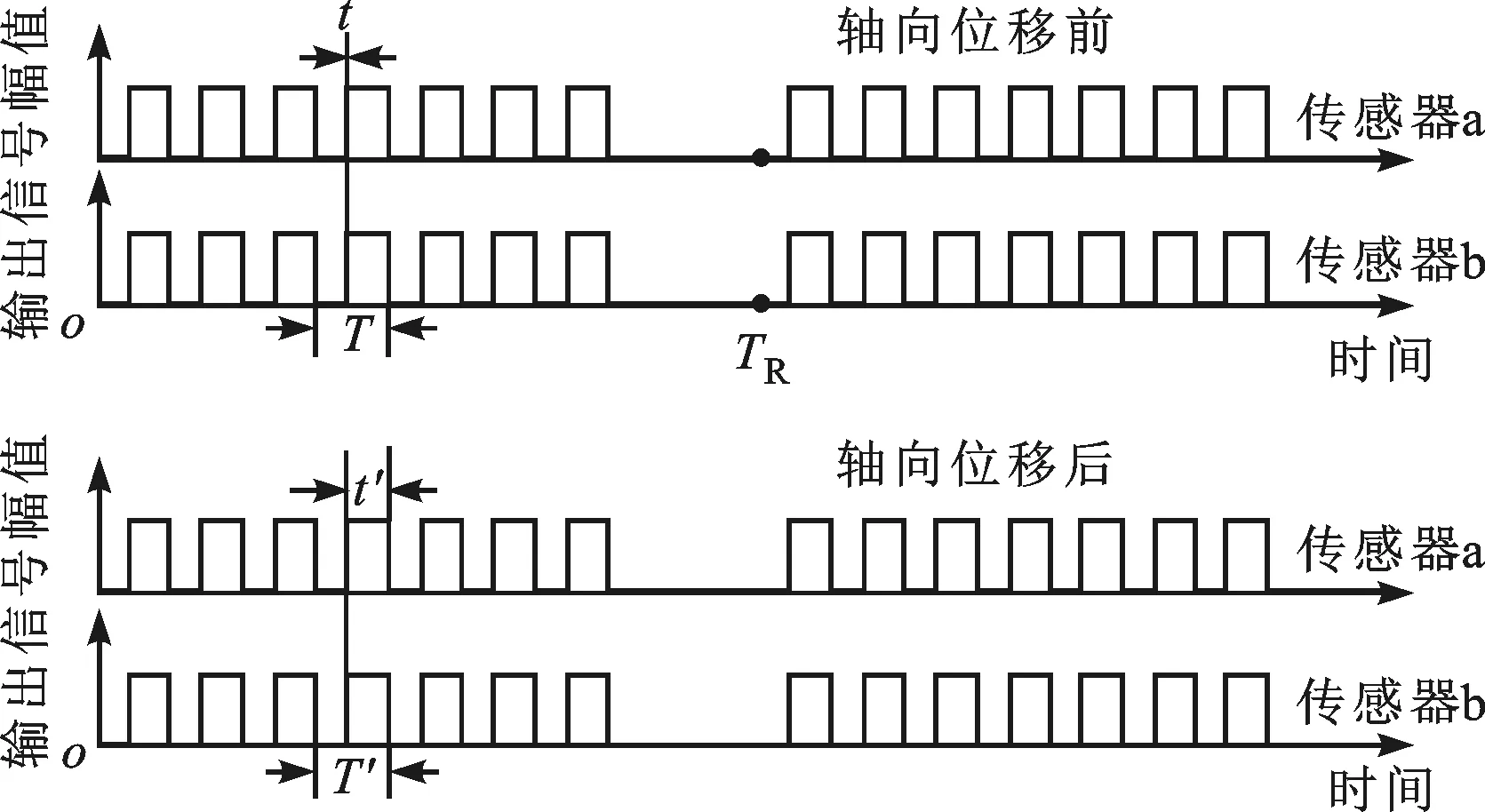
(b)传感器输出信号对比图4 轴向位移前后传感器输出信号示意图
联立式(1)和式(2),可得转子的轴向位移
(3)
由式(3)可知,转子产生的轴向位移可以通过条码的尺寸参数和两路传感器输出信号的时间延迟计算得到。显然,条码宽度、条码倾角等参数会对测量结果产生影响,因此需要进行仿真实验,探究不同参数对测量结果的影响。
2 位移测量误差仿真分析
2.1 测量条码模型的建立

图5 时间延迟法测量条码模型
由于打印机打印速度、送纸平稳性等的影响,实际打印条码边缘并非一条绝对的直线,而是在一定的区间范围内波动。考虑条码边缘的波动性,认为条码边缘误差服从均值为0、幅值为δw的正态分布。考虑条码边缘波动并由几何关系可知,V型条码的边缘满足
Li:y=tanβ[x-(i-1)w+rand(-δw,δw)]
(i-1)w≤x≤(i-1)w+bcotβ
(4)
w0+(i-1)w≤x≤w0+(i-1)w+bcotβ
(5)
2.2 转子运动模型的建立
为了简化分析模型,本文认为转子在运转过程中为理想圆柱体,转子的实际运转规律为转子运转过程中的倾斜角、偏心距、转动角速度、轴向振动和轴向位移等运动参数单独作用结果的叠加。
转子倾斜角γ和偏心距e对转子的作用由转子坐标系o1x1y1z1在基座坐标系o2x2y2z2内的初始位置确定。设转子坐标系的y1轴与基座坐标系y2轴的夹角为转子倾斜角γ,转子坐标系原点o1和基座坐标系原点o2的距离为偏心距e,如图6所示。
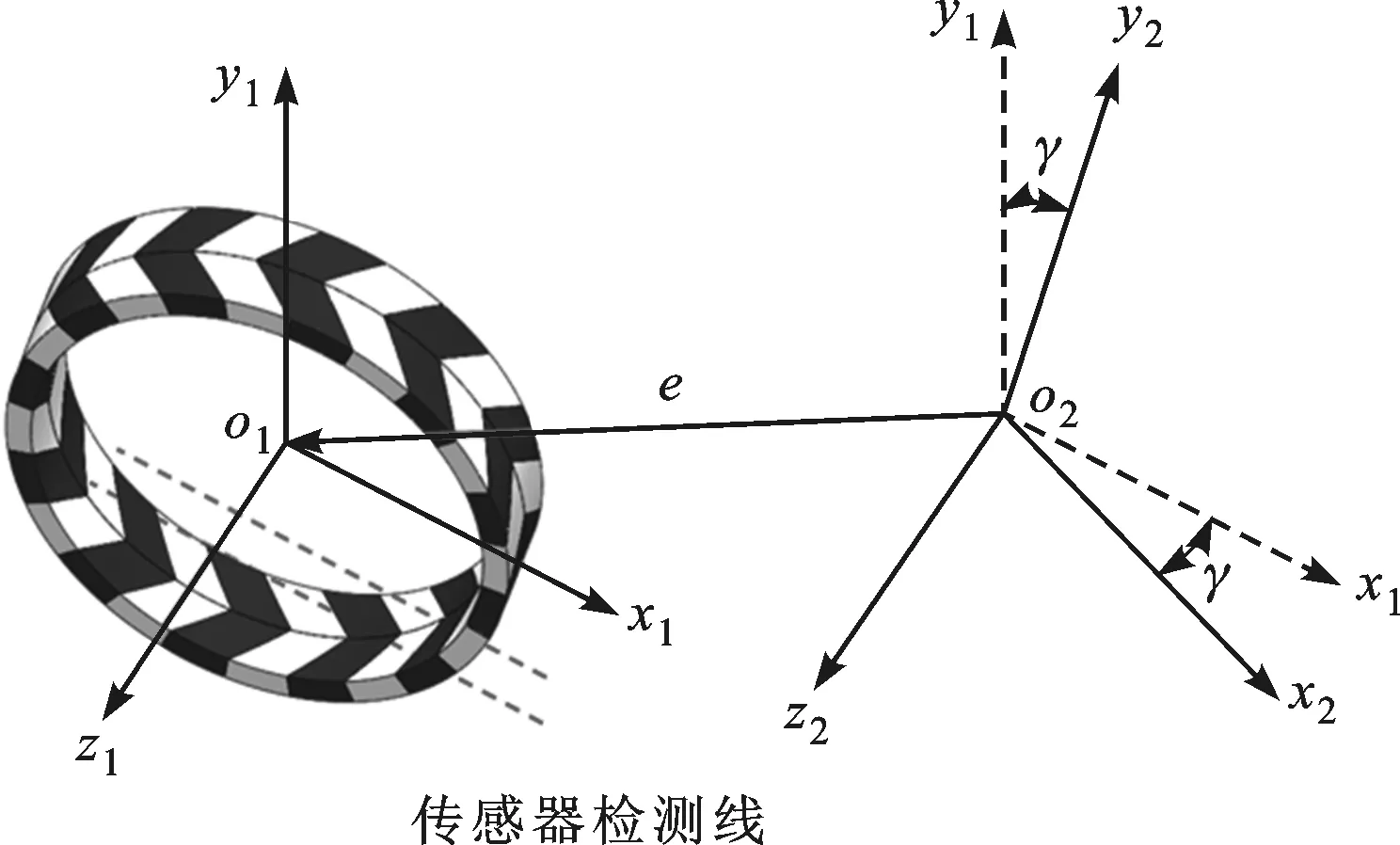
图6 转子坐标系与基座坐标系的相对关系
记e=(ax,ay,az),通过坐标变换的关系可得,转子坐标系下任意一点(x1,y1,z1)与基座坐标系下的坐标(x2,y2,z2)满足关系式
(6)
转动角速度ω相当于对转子坐标系o1x1y1z1绕着z2轴旋转,轴向振动b和轴向位移z对转子的作用相当于转子所在的坐标系o1x1y1z1沿着z2轴方向的平移,因此作用前后转子上各点的坐标满足
(7)
式中:(x1,y1,z1)为旋转前转子上各点坐标;(x2,y2,z2)为旋转后转子上各点坐标。
2.3 仿真模型求解
此数学仿真模型的主要求解思路为:
(1)输入工况参数(条码尺寸、转子安装尺寸、运转参数等);
(2)根据传感器检测到的测量条码颜色得到初始时刻传感器输出;
(3)求解下一采样时刻的转子位置;
(4)求解此时刻的传感器输出,保存结果,然后循环执行(3)和(4),直至到达预定测量时间。
计算流程如图7所示,在仿真过程中,可以通过模型计算得到测量条码边缘,然后通过计算得到传感器测量线与条码边缘的位置关系,确定此时条码的颜色,并得到此采样时刻的传感器输出。

图7 仿真计算流程图
2.4 仿真结果分析
利用仿真模型计算条码倾角β、条码数量、转子转速、位移变化对测试结果的影响。仿真时,设置模型的典型参数如下:条码倾斜角度β为60°;条码宽度w0为10 mm;转子偏心距e、转子倾斜角γ、轴向振动均为0;轴向位移z为1 mm;转子转速为600 r/min。未具体说明情况下,仿真计算中的工况参数都以上述的参数典型值为例。
(1)条码倾角β。倾角变化引起产生相同轴向位移的时间延迟量不同。以计算位移与设定位移之差的峰值作为误差评价指标,倾角对测试结果的影响如图8所示。

图8 倾斜角度对测试误差的仿真分析结果
由图8可得,条码倾斜角度越大则误差越大,测量准确度越低,这是由于条码倾角越大,条码边缘越陡,则边缘检测的误差越大。但是,条码倾斜角度过小会使得条码边缘容易损坏,制作困难。因此,在位移测量中,为提高测量精度,在现有制作条件下,尽可能减小条码倾斜角度。
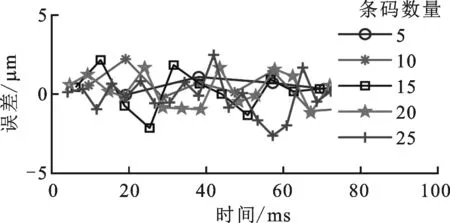
(2)条码数量。在待测转子直径确定后,条码总长度确定,条码数量增多会使测试条码的宽度w0相应减小。根据位移测量原理,每经过一个局部周期,可以进行一次轴向位移计算,所以条码数量增加可以提高轴向位移的计算响应速度。仿真时,条码测量区宽度不变,改变测量条码数量得到如图9所示的仿真结果。
仿真结果表明,测量误差与条码数量无关,随着条码数量增加,响应时间降低。实际测试中,为提高响应速度,选用条码宽度较小的条码。
(3)转子转速。转子转速对测试结果的影响主要在于转速不同会导致脉冲宽度发生变化,从而对轴向位移计算产生不同的影响。利用仿真分析模型计算得到不同转速下的误差峰值如图10所示。
(a)不同条码数量时的轴向位移计算误差

(b)条码数量与响应时间关系图9 条码数量对测试结果的影响

图10 转速对测试误差峰值影响的仿真分析结果
由图10可知,测量误差随着转速的增加而增大,因此在应用中,高速测量时会具有较大的误差,需要考虑通过信号处理等手段对误差进行消除,提高测量精度。
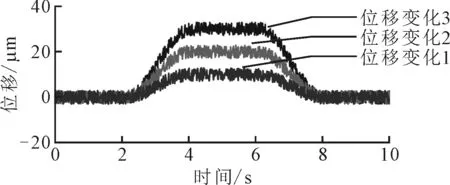
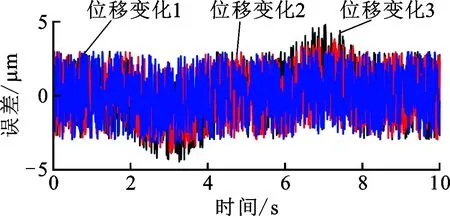
(4)位移变化。为仿真轴向位移随时间发生变化时的位移测量结果,设置模型在前2 s的位移为0,在2~4 s位移逐渐增大,4~6 s位移保持不变,6~8 s位移逐渐降低,8~10 s位移不变,仿真结果见图11。
从图11可以看出,误差在位移变化过程中增大,位移增大时误差为负值,位移减小时误差为正值,位移变化速度越大,误差峰值越大。
通过模型仿真可以看出:轴向位移测量精度随着条码倾斜角度的增大而降低;条码数量增加,位移测量结果的计算响应速度会相应提高但对测量精度的影响较小;变转速情况下的位移测量误差会随着转速增加呈线性增加的趋势;变位移情况下,位移测量误差随变化速度的增大而增大,位移停止变化之后误差又有所降低。从上述分析可以看出,转速对测量结果精度的影响最大,低转速下测量结果与高转速下测量结果误差可相差一个量级,因此需要通过其他手段抑制高转速带来的较大误差。
(a)位移计算结果
(b)位移计算误差图11 位移变化时的测量结果
3 实验测试
3.1 实验装置
实验测试平台如图12所示,采用电主轴驱动,转子由空气轴支承。由于实验采用的高精度空气轴在加载时的轴向位移较小且不易控制,故采用移动传感器的方法实现转子相对于传感器的轴向位移。将激光光纤色标传感器固定于传感器支架上,通过手轮调节微位移平台移动,使得传感器相对转子产生轴向位移。同时,利用高精度激光位移传感器(测量精度可达±0.5 μm)检测传感器支架的一端,得到转子实际轴向位移。通过计算得到的轴向位移与激光位移传感器直接测量得到轴向位移的差值即为测试误差。

图12 位移测量实验台
测位移时,通过激光光纤传感器将光信号转化为电压信号,然后经调理电路后得到两路时域脉冲信号,根据两路传感器输出信号的时间延迟,计算转子轴向位移。
3.2 测量结果分析
为了验证本文提出位移测量方法的有效性,从而得到测量精度,通过分析不同工况对位移测量结果的影响,开展不同工况下转子轴向位移测试实验研究,以计算得到的轴向位移和高精度激光位移传感器直接测量得到的位移之差绝对值的最大值(误差峰值)作为误差的评价指标。
(1)条码倾角β。转子转速分别为200 r/min和1 000 r/min时,测量误差峰值与测量条码倾斜角度关系如图13所示。从图中可以看出,条码倾斜角度与位移测量误差峰值具有一定的相关性,倾斜角度越大,误差峰值越大,精确度越低;同一倾角下,转速为1 000 r/min时的误差峰值较转速为200 r/min时大,侧面说明当转速越高的时候,位移计算结果的误差越大。
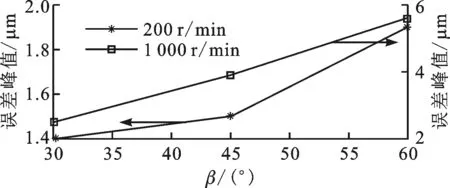
图13 误差峰值与条码倾角的关系
(2)条码宽度w0。理论上每经过一组条码即可计算得到一个轴向位移,因而条码宽度引起条码数量的变化,最终会引起计算结果响应时间的变化,如图14所示。

图14 条码宽度、转速与响应时间的关系
从图14可以看出,在转子转速一定的情况下,条码宽度越大,测量区条码数量越少,位移计算结果的响应时间越长;在条码宽度一定的情况下,转子转速提高,位移计算结果的响应时间越少。另外,在条码倾角确定的情况下,条码宽度对测量误差的影响如图15所示,说明条码宽度的变化对误差峰值的影响较小。

图15 条码宽度对位移测量结果的影响
(3)转子转速。转子转速变化会引起条码测量区信号局部周期的变化,从而引起转子运动状态参数的变化,这在一定程度上使位移测量结果的误差发生变化。使用倾斜角为30°、宽度为7.5 mm的测量条码进行位移测量,测量误差与转子转速关系如图16所示。
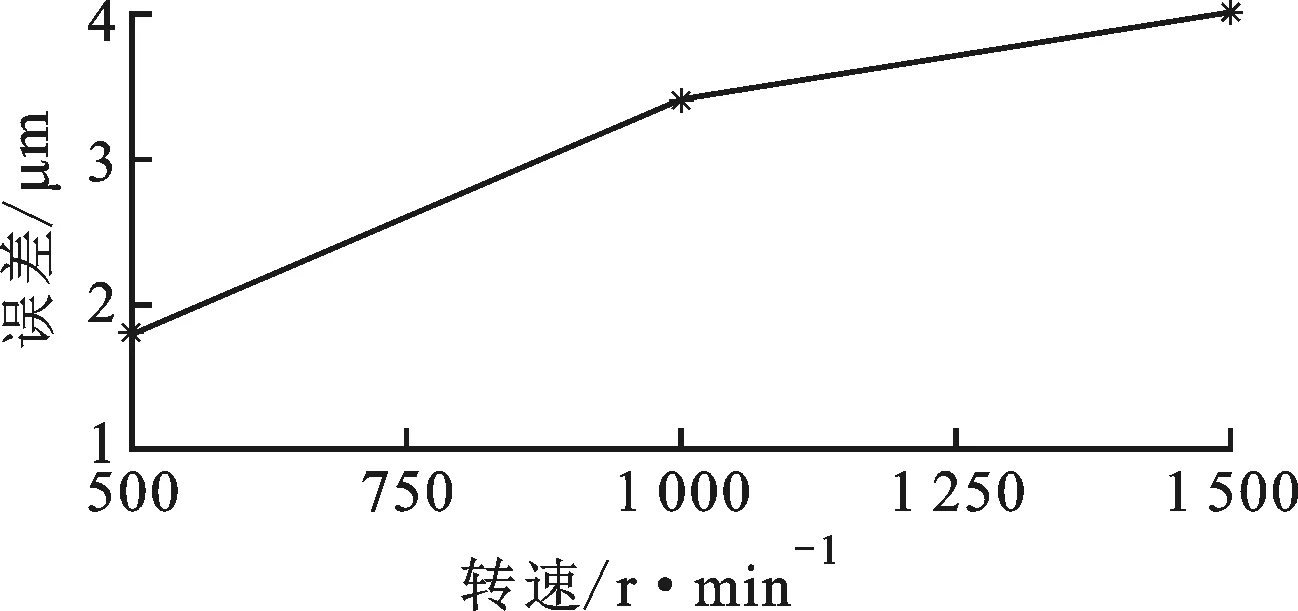
图16 转速对位移测量结果的影响
从图16可以看出,当转速越高的时候,位移计算结果的误差越大。
(4)位移变化。使用倾斜角为30°、宽度为7.5 mm的测量条码进行位移测量,实验时的转子转速为200 r/min,在第10 s和第20 s时,转子位移快速变化,用于验证测量结果的响应情况,测量结果如图17所示。

(a)位移变化较快时的位移

(b)位移变化较快时的位移测量误差

(c)位移变化较慢时的位移
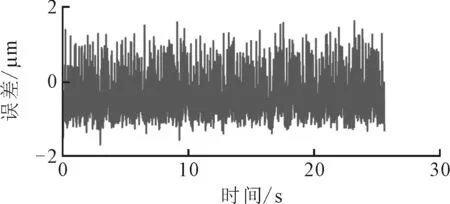
(d)位移变化较慢时的位移测量误差图17 转子转速为200 r/min时位移测量结果
(1)由于实际打印条码边缘并非一条绝对的直线,而是在一定的区间范围内波动,导致计算位移在实测位移附近上下波动。
(2)当位移变化的速度较快时会产生很大的误差,当位移变化结束之后,误差又会有所下降。在位移快速增大的过程中,位移测量误差为负值,位移快速减小的过程中,位移测量误差为正值。
(3)位移变化速度较慢时,位移测量结果在位移变化过程中的误差较稳定,测量误差在2 μm以内,具有较高的测试精度。
通过上述结果分析可知,导致图17b所示的位移快速变化过程中误差急剧增大的原因是,位移计算结果与实际位移之间产生了时间延迟。图14表明,转子转速升高时,测量结果的响应速度会提高,因此将转子转速设定为1 000 r/min,通过提高转速来提高测试的响应速度,进一步验证上述分析结果,测量结果如图18所示。
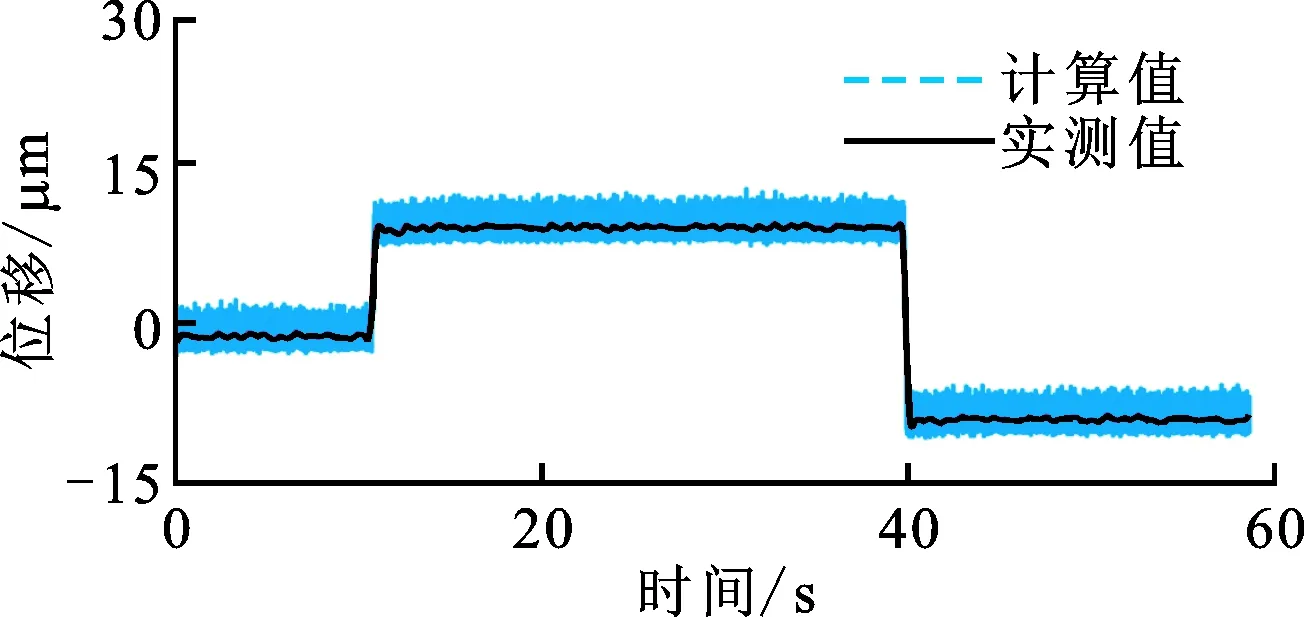
(a)位移变化较快时的位移

(b)位移变化较快时的位移测量误差

(c)位移变化较慢时的位移
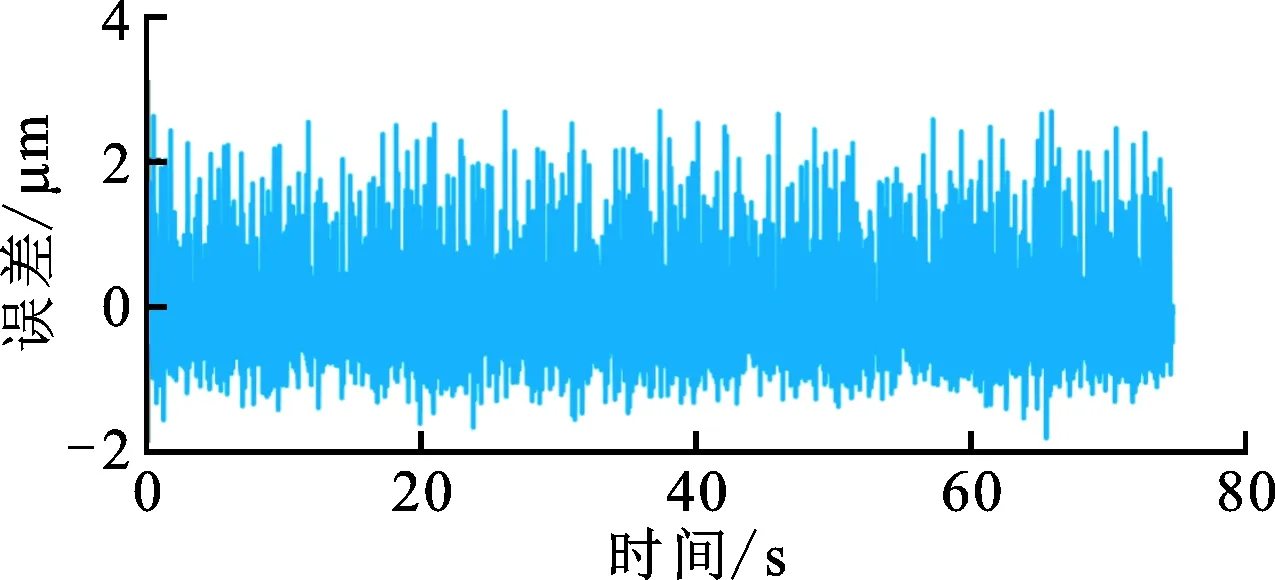
(d)位移变化较慢时的位移测量误差图18 转子转速为1 000 r/min时位移测量结果
在转子转速为1 000 r/min时,转子位移快速变化时的误差突变量在5 μm以内,相比低转速下的位移突变量有效降低。这说明,提高计算响应速度可以在一定程度上降低位移测量误差,提高测试准确度。
对比图17b和图18b不难发现,转子转速提高,位移快速变化过程中的位移测量误差由10 μm左右降低到5 μm以内。当转子转速提高之后,位移计算结果响应速度提高,位移计算结果的延迟不再明显。
综上所述,本文方法在转子位移变化慢的情况下误差稳定,转子转速在1 000 r/min条件下,测量误差在5 μm以内,满足工程要求。这个结果说明,适当提高转子转速可以降低转子位移快速变化时的误差突变量,提高测试精度。
4 结 论
(1)提出了基于时间延迟测量原理的转子轴向位移径向测量方法,设计了基于打印条码和光学传感器的测量方案。
(2)基于理论仿真和实验测试对比研究,在1 000 r/min条件下,测量误差在5 μm之内,具有一定的监测精度。
(3)受打印条码边缘波动等因素影响,目前的测量精度在5 μm。即使如此,该测量方法仍然适用于汽轮机转子、大型磁悬浮轴承、汽车轮毂轴承等系统的轴向位移测量需求,尤其是在轴向空间严重受限的场合具有突出的应用优势。
在后续的工作中,将对高转速情况下条码边缘高精度检测方法进行深入研究,同时,将增加对打印条码精度的分析,研究打印条码尺寸精度、边缘质量及高速下条码的离心变形等因素对监测精度的影响,以期达到亚微米级的测量精度,满足智能轴承等转子集成化、高精度轴向位移测量要求。
