薄壁平面件真空多孔吸具的力学特性与优化设计

杨金川,张建富,李杰,谢强,冯平法

(1.清华大学机械工程系,100084,北京;2.中国工程物理研究院材料研究所,621700,四川绵阳)

薄壁平面件(径厚比大于50或壁厚小于等于2 mm),特别是精密物理实验超精密零件,具有刚度低、壁厚小(大于0.1 mm,小于2 mm)等特点。卡盘或卡爪等在装夹中存在限制,易产生严重的装夹变形,从而影响工件加工质量[1-3]。对于高压微喷、爆轰性能检测等精密物理实验所需超精密薄壁平面件,装夹变形引起的形位偏差将直接影响实验效果[4-5]。

为了克服薄壁类零部件装夹过程的难点,多数情况下,需根据零部件形貌尺寸并结合制造工艺路线,进行特定工装的开发,通用性较低[6-8]。其中,最常用的是采用数值仿真模拟薄壁类零部件的装夹状态并规划装夹工艺流程,然后根据仿真结果研发相应工装[9-11]。早期King等基于工装的刚体化,利用非线性技术优化工件装夹定位布局[12]。针对薄壁件加工的特定区域定位误差及变形,王少锋等提出了一种跟随加工区域布置定位点的定位新方法,为支承和定位点布局全局优化提供优化初值[13]。为避免传统机械工装在装夹时引入较大装夹变形,真空吸附技术已经在小型或规则形状薄壁零部件装夹中开始较大范围应用[14-16]。此外,刘春青等提出了一种确定薄壁件在多点柔性定位时参数选择和吸附压力的寻优算法,以实现最优选择[17]。

上述各方法基于弹性力学均提出了优化算法或模型,明确了局部以及特定设计变量。但是,对于超精密加工薄壁平面件真空吸附装夹过程,仍需进一步分析在任一瞬时切削力(在一个切削点处)作用下的变形,并将吸具研制、零件材料及切削力状态纳入整体考虑。本文结合材料力学与有限元法,建立真空平面多孔吸具的优化设计方法,才能更全面建立整个表面的变形加工误差控制模型。

1 薄壁平面件吸附装夹受力分析

1.1 平面件静止受力状态

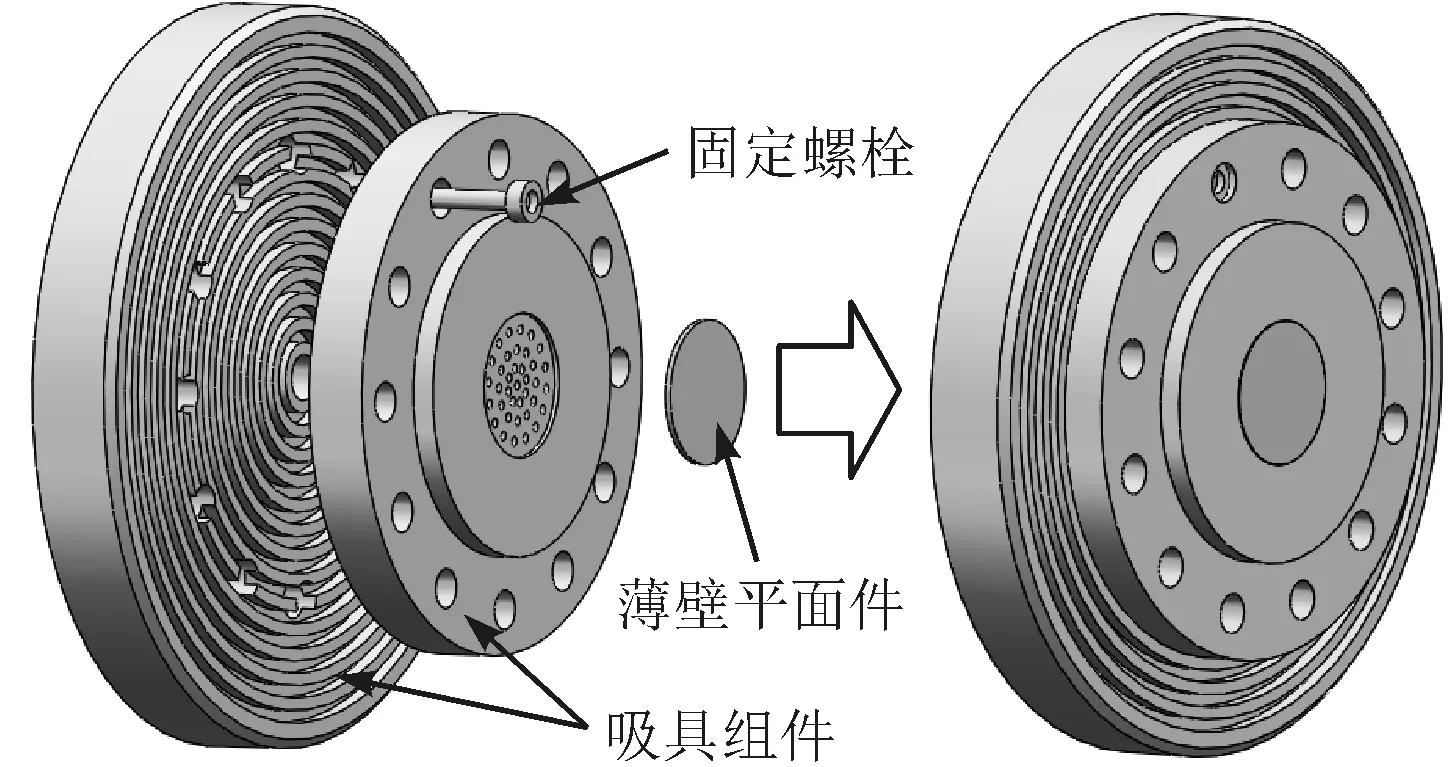
图1 多孔平面真空吸附装夹状态

加工前,将薄壁平面件采用真空多孔平面吸附方式装夹于吸盘,装配过程及装夹状态如图1所示。薄壁平面件吸附于吸盘平面后,在吸孔区域的受力状态如图2所示。

q为真空度,即大气压强P1和真空负压P2的差值,q=P1-P2;δ为工件受压变形后的挠度;t为工件厚度;r为真空吸孔半径;R为薄壁件半径图2 平面件受力分布状态

由图2可知,平面件内接触面受到负压P2,待加工面受到空气压强P1。平面件可等效为圆周简支平面圆板模型。根据轴对称载荷圆周简支平板变形理论[18],可得出均布载荷作用下的平面件吸孔区域的静态变形挠度方程为

(1)

式中:rx为孔中心到计算点的径向距离;μ为材料泊松比;D′为平面件等效抗弯刚度,公式为

(2)

其中E为材料弹性模量。

如图2所示,薄壁平面件在吸孔处发生径向和轴向变形,并产生径向和轴向应力,分别为

(3)

上述各式即可表征薄壁平面件加工前初始吸附固定后的静力学状态。

1.2 平面件切削受力状态

薄壁平面件采用单点金刚石超精密车床进行横车加工。在超精密切削条件下,进给量f远大于切削深度ap,因此可用典型单点金刚石切削模型来研究切削过程[19]。切削过程存在3个切削分力,即主切削力Fc、切深抗力Fp与进给力Ff,如图3所示。

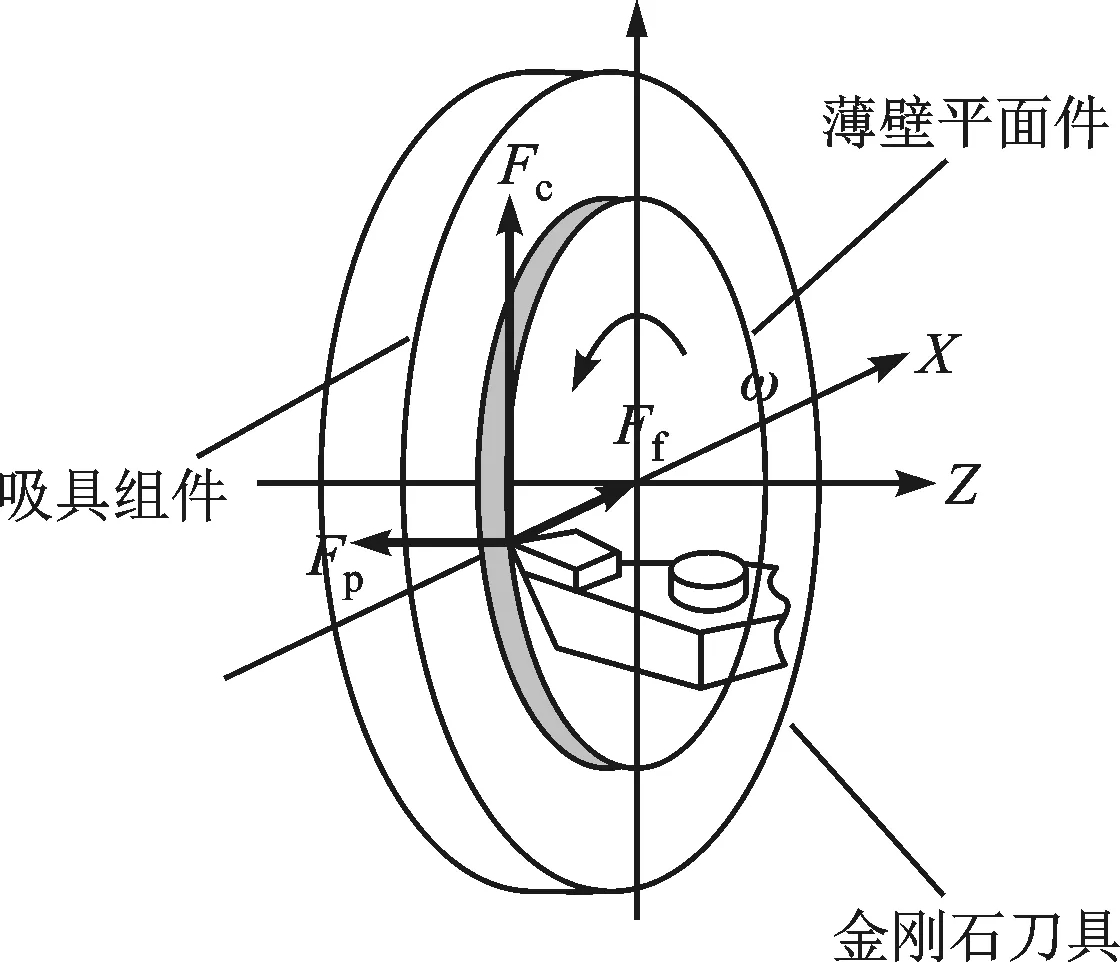
图3 横向车削及切削力状态

由于超精密加工时的切深抗力Fp在切削合力中占较大比例,因此切深抗力Fp对薄壁平面件的变形影响不可忽略[20]。根据经验公式,可得出单点金刚石恒线速车削6061铝合金的Fc、Ff与Fp的计算公式为[21-22]

(4)

式中:ω为主轴转速,r/min;f为进给量,mm/s;ap为切削深度,μm;Fp取最大比率0.7进行验证计算。

刀尖产生的切深抗力Fp作为集中力引起的变形可采用直角三角形进行拟合,得出吸孔刀尖切削区域的动态变形挠度为[23]

(5)

由此可知切削力最大处在平面件边缘位置。同理,切深抗力Fp作用于吸孔中心时,切削过程也产生径向应力σQJ和轴向应力σQZ,表达式分别为

(6)

式中:rb为最大应力位置距真空吸孔边缘的距离,值为

rb=r-b

(7)

其中b为刀尖与工件接触半径,μm。根据超精密车削微观表面形成机理[24],刀尖与工件接触半径b的理论值为

(8)

式中:rD为刀尖圆弧半径,μm。

式(1)～式(8)即可表征薄壁平面件真空平面吸附装夹的切削及非切削时的受力变形状态。

2 吸附装夹与切削稳定性

对于半径为R的吸附平面,在表面加工半径为r的真空吸孔,令径向各孔圆心位置距离为s1,同一径向位置上相邻两孔的距离为s2,如图4所示。

图4 圆平面吸孔位置布局

图4所示的尺寸与几何参数与圆平面内可加工的吸孔圈数n之间的关系为

(9)

式中:n=1,2,3,…。当n=1时,仅存在一个中心吸孔;使式(9)成立的n的最大正整数即为圆平面可加工的最大吸孔圈数。

在360°圆周范围内,第i圈能够加工的均匀分布的最大吸孔数mimax,可根据圆心角弦长公式得出

(10)

由式(9)(10),可得平面上可加工的吸孔总数为

(11)

式中:mi是第i圈实际加工吸孔数。加工后的圆平面与工件表面接触时,实际接触总面积为

A=πR2-πr2N

(12)

接触区域受到的实际接触压强为

(13)

已知薄壁平面件保持平衡的充要条件是任意瞬时所受力及力矩均平衡,数学表达[25]为

(14)

式中:Fi为支撑力;Fj为大气压力;Fm为径向静摩擦力;rm为任意点距工件中心轴距离。

2.1 切削状态装夹稳定性

(1)在明确切削周向稳定性条件之前,需要明确平面件周向所受力及力矩作用。吸孔区域微圆弧静摩擦力矩计算区域见图5。

Ri为第i圈吸孔圆心所在虚拟圆半径;Rix为以圆平面圆心在径向距离吸孔y处的虚拟圆半径;β为微圆弧段所对应的圆心角图5 吸孔区域微圆弧静摩擦力矩计算区域

由图5可知,y方向dy所属微圆弧段部分的面积为

dA0=Rixβdy

(15)

该微圆弧一圈的实际接触面积为

dAi=2πRixdy-miRixβdy

(16)

在均布压强P,则任微圆实际接触面积dAi所产生的摩擦力矩为

dLifm=dAiPRixη

(17)

式中:η为铝合金之间摩擦系数。第i圈吸孔所在圆环区域产生的摩擦力矩为

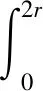
(18)

所有吸孔在区域产生的总摩擦力矩为

(19)

可得工件实际接触区域的总摩擦力矩为

(20)

相邻吸孔圈之间的区域如图6所示。该类区域需区分内圆环面与单一吸孔及最外圈吸孔的外围部分,即2≤i≤n-1与i=1或n两种情况。

Rimin为第i圈的最小半径值;Rimax为第i圈的最大半径值;Rx为环接触区域中y处的半径图6 圆环接触静摩擦力矩计算区域

计算得到圆环接触面的总静摩擦力矩为

(21)

又知周向产生的总摩擦力矩Lf由吸孔所在圆环带的实际接触面积产生的总摩擦力矩Lf1与圆环接触面的总摩擦力矩Lf2之和组成,即

Lf=Lf1+Lf2

(22)

由图3及式(14)可知,工件保持周向稳定需要保证实际接触面产生的静摩擦力矩Lf与工件周向所受到的外作用力矩平衡,即需要满足条件为

Lf≥FcRS

(23)

式中:S为吸附稳定系数,取值为2。

(2)工件所受径向力有主切削力Fc、重力G、静摩擦力Fm以及进给力Ff。加工过程需要保持竖直径向与水平径向的力平衡,根据式(14),有

(24)

由式(24)便可判定薄壁平面件的径向稳定性。其中,静摩擦力Fm为

Fm=PAη

(25)

(26)

式中:f-1(Lf)和f-1(Fm)分别为式(24)和式(25)中真空度q的反函数。

2.2 设计目标函数及其约束条件

薄壁件装夹状态与真空吸具的孔径r、真空度q二者有关。因此,以最小切削深度apmin等效为平面度要求δP、平面件厚度t为前置设计变量,真空度q为过程设计变量,设计过程如下。

(1)由式(1),可得吸孔半径r设计目标函数为

(27)

对于任意真空度q,r的设计约束条件为

r≤max(r)

(28)

(2)预设s1与s2确定平面吸孔数量。

(4)变形约束条件:超精密加工切削深度最小值apmin与加工后平面度限制δP比较,取二者最小值。因此,加工前静态吸附变形δJ限制条件为

δJmax≤min(apmin,δP)

(29)

(5)加工应力约束条件:在切深抗力Fp与均布载荷q的双重作用下,为了防止加工中轴向应力引起吸孔区域的轴向塑性变形,加工过程的动态应力最大值σmax的约束条件为

σmax=max(σJZ+σQZ)≤σe

(30)

其中6061铝合金在温度为240°时的弹性极限σe=240 MPa[26]。根据式(30)验证并限制其切削状态下的装夹与加工应力,以控制工件外形精度。

综上,式(27)～式(30)构成了真空多孔吸具吸孔孔径2r、真空度q的共同设计准则与验证方法。

3 吸具优化设计

前置设计变量及工艺参数:薄壁平面件材料为6061铝合金,泊松比μ=0.33,弹性模量E=68 GPa,半径R=25 mm,坯件厚度t=2 mm;吸具材料为2A12铝合金;铝合金之间的摩擦系数η=0.22;切削深度ap=(1～10) μm;进给量f=(5～20) mm/min;恒线速走刀,主轴初始转速ω=5 000 r/min,最大转速15 000 r/min;加工后表面平面度δP≤1 μm。

优化设计步骤如下。

(1)根据实际操作规程,真空度q的实际可调范围是(0.001～0.1) MPa。由式(28),可得apmin条件下,当真空度分别为0.1 MPa和0.001 MPa时,吸孔最大可选半径rq0.1=7.984 mm和rq0.001=25.246 mm。根据式(28),可得吸孔半径优化设计范围,即

r≤min(rq0.1,rq0.001)

因此,可预设吸孔孔径r=1 mm。

(2)根据图6,初设s1=4 mm,s2=4 mm,可得平面内吸孔总圈数n=6,各圈分别可加工的最大吸孔数分别为1、6、12、18、25、31。数控编程优化后,各圈加工吸孔数mi=1,8,12,16,21,24。

(3)由式(4),可得各切削分力的理论最大值Fcmax=0.545 N,Ffmax=4.267 N,Fpmax=0.789 N。

(4)将上述理论值带入式(30)及式(28),验证动态应力最大值σmax的约束条件,可得

σmax=(0.32×10-6q+0.55)≪σe

由结果可知,切深抗力和均布载荷引起的轴向动态应力小于弹性极限,变形属于弹性应变。考虑真空度控制范围,可以认为上述判定合理。

(5)根据预设加工吸孔尺寸和吸孔数量以及式(23)(24)(26),分别验证周向及径向稳定性,可得真空度q的控制下限qmin=0.0198 MPa,由此可预设真空度q的控制值为q=0.03 MPa。

(6)通过有限元验证工件装夹变形。薄壁件与真空吸具均采用C3D10(六面体)三维应力实体单元,且吸具简化为刚体。负压均布载荷q作用下的状态以及真空吸附加载后的仿真变形效果分别如图7和图8所示。

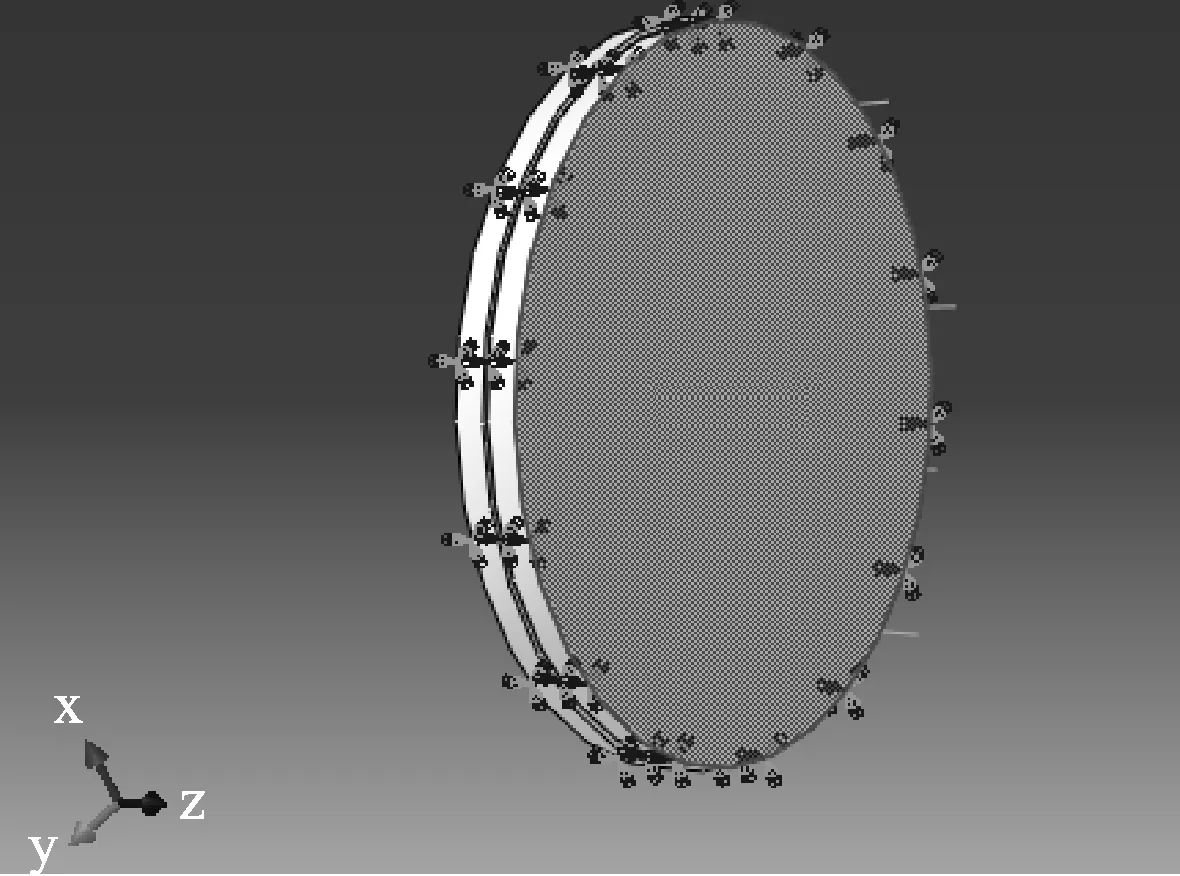
图7 吸附受力状态的有限元模型

图8 吸附受力状态仿真结果

由图8可知,在真空度q=0.03 MPa时,吸孔区域的静态最大变形量δJmax≤2.125 nm,吸孔中心平均变形量为1.539 nm。

采用理论计算和仿真分别得到的变形量均在nm量级,基于激光传感器精度并结合理论与仿真误差以及材料接触等因素,可认为计算和仿真结果基本一致。由此基于该优化设计方案研制的吸具样件及吸附装夹效果如图9所示。

(a)装夹前吸具样件 (b)装夹后吸附状态图9 吸具样件与吸附状态

图10 平面件测量点分布位置

车削试验完成后采用Form Talysurf PGI1240(分辨率为0.8 nm)测量加工后厚度为1.8 mm的薄壁平面件,测量点分布位置如图10所示。

图10中,一共布点36个,测量时首先测量O11并以该值为基准0点,相对值为0,后续测量各点与O11取差值,获得的各点高度差数据如表1所示。

表1 平面件各测量点与O11测量数据差

经计算得出,平面度实际公差为418.15 nm。位于同一同心圆位置的测量点高度差小于30 nm,靠近中心位置,由于线速度减小,高度差出现增大。

根据图8和表1所示,考虑加工及测量误差,可以认为该真空吸具的结构优化设计是合理有效的,满足薄壁平面件超精密加工安装定位的变形控制与平面度需求,能够实现稳定吸附装夹。

4 结 论

(1)吸具吸孔设计布局与真空度影响薄壁平面件加工的静态力学变形。在工件尺寸确定的情况下,吸孔的数量越少,孔径越小,所需真空度越大;吸孔布局确定之后,真空度越大则薄壁平面件装夹及切削过程变形越大。

(2)在吸附装夹与切削过程中,工件变形主要产生在吸孔区域,越靠近吸孔中心,工件变形量越大,且吸孔中心位置的变形量最大。

(3)吸孔设计以及吸具的设计布局额外受到实际加工能力的制约。因此,在对吸具进行优化设计时,必须将吸孔实际加工能力纳入设计考量。