数学解题规避分类讨论的几种思路
2019-04-04王健发
王健发
(广东省惠州市华罗庚中学 516000)
分类讨论是一种重要的数学思想,不仅要灵活运用数学基本知识与方法,同时对思维的深刻性和严谨性提出了很高的要求. 活跃在各类考试的舞台上,综合性强,学生普遍感到棘手. 学生由于对分类原则考虑不全导致顾此失彼. 本文结合高中所学知识介绍几种规避分类讨论优化解题的思路,期望对大家有所帮助.
一、灵活运用公式
例1 解不等式|x+log2x| 解由|a+b|≤|a|+|b|,知当且仅当ab≥0时,等号成立,从而x·log2x<0.又x>0,所以log2x<0.故解集为x∈(0,1). 例2 设a>0,a≠0,0 证明因为0 又因为|loga(1-x)|-|loga(x+1)| 所以|loga(1-x)|>|loga(x+1)|. 例1和例2 都含有绝对值和对数,一般而言需要讨论绝对值内代数式的正负以及对数中底数a>1或0 例3 若p∈R,且当|log2p|<2时,不等式px+1>2x-p恒成立,试求x的取值范围. 本题若用常规方法,以x为主元,则需分类讨论,而以p为主元,可避免讨论. 例4 等比数列{an}的前n项和为Sn. 若S3+S6=2S9,求公比的实数值. 解由Sn=Sm+qmSn-m(n>m),得S6=S3+q3S3,S9=S6+q6S3=S3+q3S3+q6S3. 因为S3+S6=2S9,所以2S3+q3S3=2(S3+q3S3+q6S3),即2q6S3+q3S3=0. 例5 等比数列前n项和为2,其后2n项的和为12,求再其后3n项的和. 解由已知得Sn=2,S3n-Sn=12,所以S3n=Sn+12=14. 又因为S3n=Sn+qnS2n=Sn+qn(Sn+qnSn),所以14=2+2qn+2q2n,解得qn=2或qn=-3. 又S6n-S3n=(S3n+q3nS3n)-S3n=q3nS3n=14q3n,所以S6n-S3n=14·23=112或S6n-S3n=14·(-3)3=-378. 例4和例5涉及到等比数列和的问题,通常要对公比q分q=1和q≠1两种情形讨论. 但是,不论公比q是否为1,我们将等比数列和的公式进行重组之后,总有Sn=Sm+qmSn-m(n>m). 用此公式解决有关等比数的前n项和的问题,常可避免分类讨论. 本题若从正面求解需分两种情况讨论:(1)两点都在椭圆外,(2)两点都在椭圆内. 若用命题的否定思想则不需要讨论,计算简洁. 对于题目中出现“至少”、“至多”、“无”等关联词,可通过命题的否定思想进行求解. 例7 当-1 解原命题等价于不等式x2-2x+3>2a(x+2)在-1 当直线绕着点(-2,0)顺时针旋转时也满足题设条件. 例8 已知函数f(x)=ex-1-x-ax2. (2)当x>0时,f(x)≥0恒成立, 求实数a的取值范围. (2)当x>0时,f(x)≥0恒成立等价于ax2≤ex-1-x在区间(0,+∞)恒成立. 令y1=ax2,y2=ex-1-x, 即当x>0时, 函数y2=ex-1-x的图象恒在函数y1=ax2图象的上方. 因为当x>0时,y2′=ex-1>0, 所以函数y2=ex-1-x在(0,+∞)单调递增. 例7是求二次函数f(x)=x2-2(a+1)x+3-4a在(-1,1)上的最小值,需分三种情况进行讨论,例8需要画出f(x)=ex-1-x-ax2的图象,经分类讨论之后确定a的取值范围,过程不但比较复杂,而且容易出错. 但例7通过分离出一次函数求解,例8通过分离二次函数求解使得问题轻松求解. 充分运用分类讨论的思想方法解题,是解题的一个重要策略,也是训练逻辑思维能力的重要手段,提高整体把握问题意识的能力. 但在有些情况下,其过程较为繁琐,因此也容易造成解题中的失误. 故我们在掌握这一方法的同时,要灵活变通,克服思维定势带来的负迁移,学会简化或避免分类讨论,以达到方法上的优势互补.二、变换主元


三、公式重组
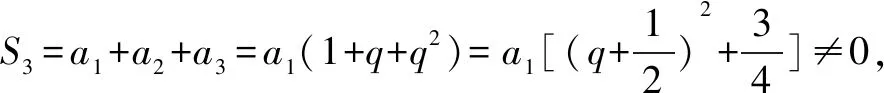
四、否定思想


五、分离函数