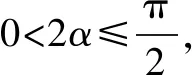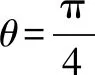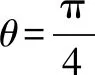立足教材 明晰方向
——挖掘教材中有价值的数学问题
2019-04-04徐照武
徐照武
(广东省珠海市实验中学 519000)
高考数学试题常常围绕考试大纲结合现用教材挖掘素材,这使得试题更具原创特点、更贴近学生实际,让学生在解题时对题目本身有似曾相识之感.实际上,命题者坚持的是选材源于教材,难度高于教材的指导思想.所以,平时教学或复习时就要立足教材,把教材中的概念、定义、定理、例习题等作为可能的试题源泉来研究,让课堂回归到数学教学的本质.
一、定义是最好的性质
数学定义是数学思维的细胞,是形成数学知识体系的基本要素.
数学中的定义,特别是解析几何中的定义,常常是一种发生定义.这种定义方法实际上就是对发生过程的一种描述.
以下是一节高二课堂小结课(也可以作为高三第一轮复习课)的一个小片段(大约需要15分钟,老师最好在课前布置给学生以下自主学习内容:例1(1)除了课本解法外,还有没有其他解法?例1(2)要求尝试多种解法).
例1 (1)(人教社实验教材(下同)必修2第122页例5)已知线段AB的端点B的坐标为(4,3),端点A在圆(x+1)2+y2=4上运动,求线段AB的中点M的轨迹方程.
(2)(2-1第37页习题2.1A4)过原点的直线与圆x2+y2-6x+5=0相交于A,B两点,求弦AB的中点M的轨迹方程.

师:我们课前布置了例1的两个小题,请各小组用两分钟时间交流.
师:先请一名同学展示你们小组的情况.

师:很好,非常好!这个解法紧紧抓住了在运动过程中的定值(圆的半径)与定点(中点N),快速找到了动点M的轨迹.同学们进一步想一想,(2)有没有简练的解法呢?
生:有.
师:好,这位同学,请说一下你的解法.
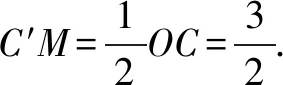
师:非常棒. 这个解法仍然紧紧抓住了在运动过程中的定值(OC)与定点(中点C′),快速找到了动点M的轨迹.(以上题目可以结合几何画板等软件演示)

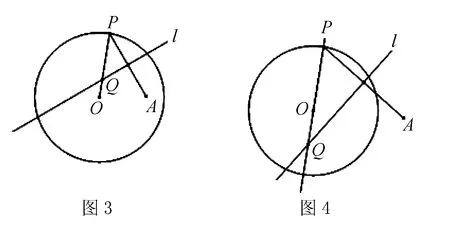
例2 (1)(1-1第42页习题2.1A7,2-1第49页习题2.2A7)如图3,圆O的半径为定长r,A是圆O内一个定点,P是圆上任意一点.线段AP的垂直平分线l和半径OP相交于点Q.当点P在圆上运动时,点Q的轨迹是什么?为什么?
(2)(1-1第54页习题2.2A5,2-1第62页习题2.3A5)如图4,圆O的半径为定长r,A是圆O外一个定点,P是圆上任意一点.线段AP的垂直平分线l和直线OP相交于点Q.当点P在圆上运动时,点Q的轨迹是什么?为什么?
师:来看例2.有了例1的求解过程,对于例2,也就水到渠成了.只要结合定圆的半径是定值及椭圆与双曲线的定义,相信大家很快就能把问题解决.
但要注意反思下面两个问题:一是(1)(2)的区别(点A在圆内与点A在圆外,垂直平分线l分为和半径OP及直线OP相交于点Q,多么美妙的一对姊妹题.这就是数学之美!),二是(2)的轨迹为什么是两支?

先给出问题的结论:
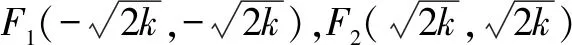
其实研究过程也非常简单:
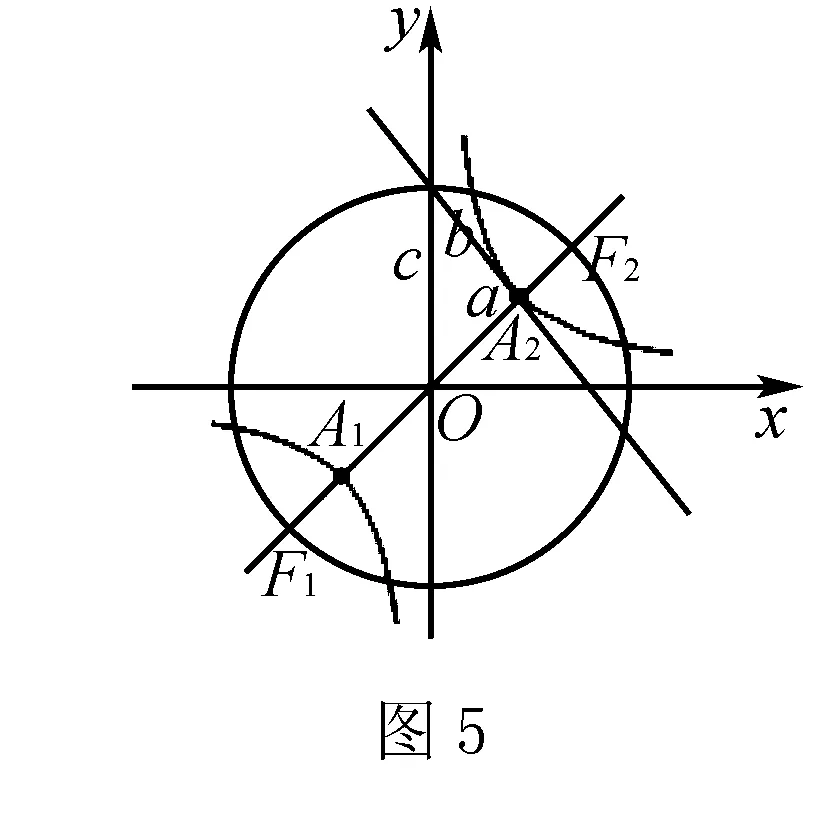
轨迹问题是解析几何的两大研究问题之一.教学时,既要考虑所有学生的数学基础,又要兼顾学生的个体差异.从最简单的情形出发,从最有利于学生数学学习的角度出发,可以让学生真正感受到数学的魅力与简洁美.以上这几个问题借助圆锥曲线(含圆)的定义都能顺利解决.(当然,利用圆锥曲线定义解题在教材及各种材料中都有非常好的归纳.)
定义是最好的性质.不但圆锥曲线的定义在解题时经常运用,离心率、等差等比数列、三角函数、斜率、向量的积等这些定义都会经常运用,并能简化解题过程.
二、尝试“小课题”研究
“小课题”研究既是一种综合性的实践活动,也是一种特殊的学习活动.开展“小课题”研究,让学生在学习过程中养成“问题即课题,学习即研究”的习惯,对于培养学生的研究意识和综合能力,促进其成长,提高学业水平,有非常积极的意义.这里的“小课题”,是加引号的“小课题”,与老师们做的“小课题”研究不是完全一样的.这里的研究目的主要是解决学生学习中出现的问题、困惑等,是以有利于他们的学习与能力的提高为目的.有时候,“小课题”甚至小到能很快解决的程度.我们也不妨把它理解为就是“研究性学习”吧!
教材是数学学科的核心教学材料,是教材编者集多代人智慧的结晶.我们要通过教材题目或材料背景进行创新,可以设问方式创新,研究角度创新,教与学方式创新等等,引导学生发现、探究、体验、反思、积累,做到举一反三,融会贯通.现行教材虽然基本上没有未解决的问题,但对于学生来说都是新鲜的.有时我们老师集几十年的“研究”仍然不能完全吃透教材与教法.下面这道课本例题,就很有研究价值.


记∠COP=θ,求当θ取何值时,矩形ABCD的面积S最大,并求出最大面积. (必修4第141页例4)
这道题目,对数学基础不是很好的学生难度已经不小了.但对学有余力的学生,在老师的指导下可以循序渐进地提出以下问题,作为课外研究性学习的“小课题”进行挖掘.
(1)矩形面积最大时OC有什么特点?(角平分线)
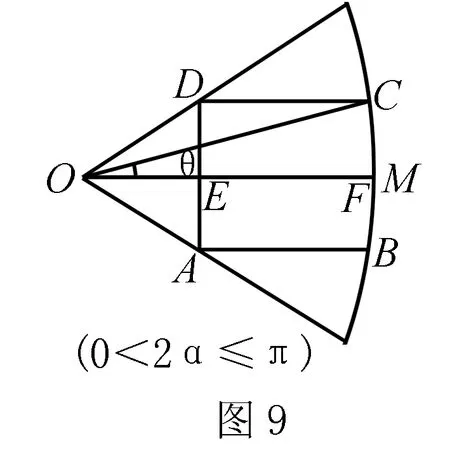
(2)如果矩形ABCD的四个顶点有两个在圆弧上,另两个在两条半径上,有没有最大面积?能利用(1)的结论得到简便解法吗?(有,可以按图9作角平分线,化为(1))
(3)以上两种解法得到的最大面积一样吗?谁最大?
(6)在中心角为2α(0<2α<2π)的扇形内怎样截出面积最大的矩形?
下面我们探讨(6)
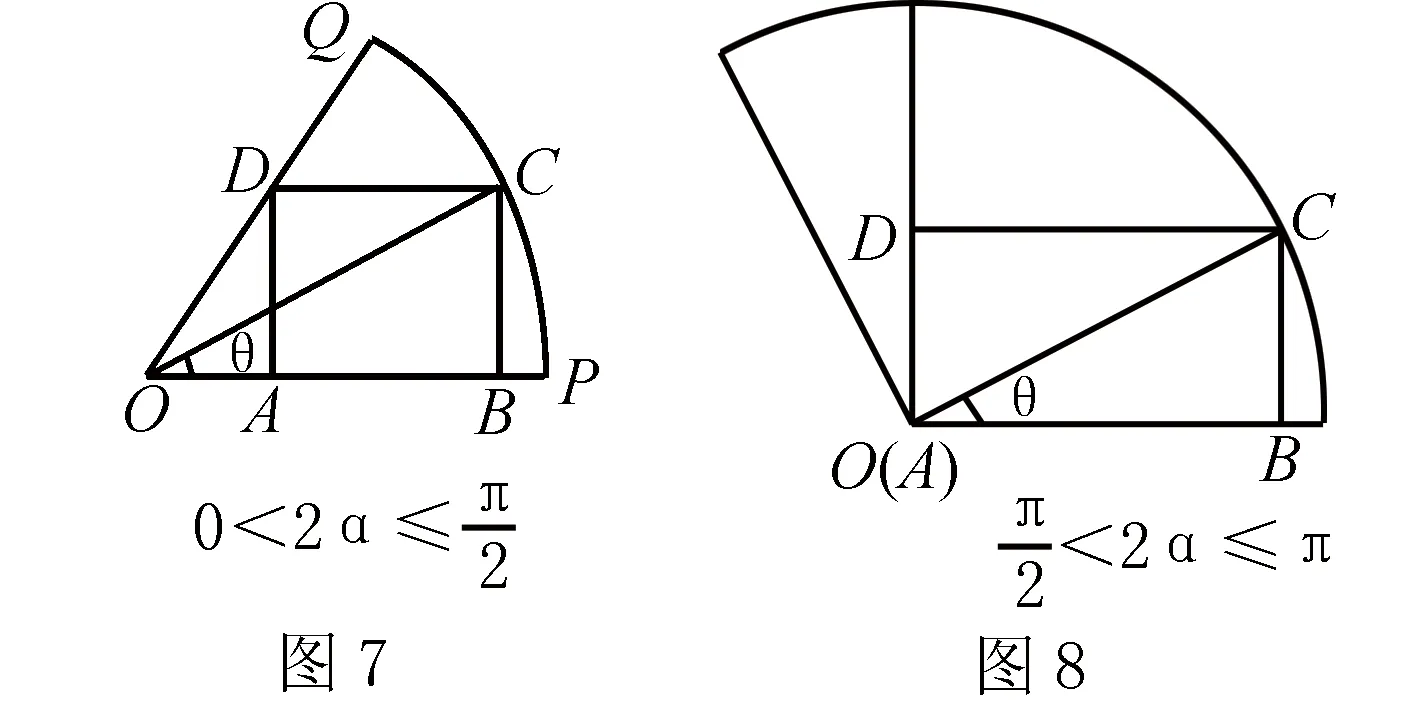
先研究0<2α≤π的情况(如图7,8 ,9).
在第一种情况下(如图7,8),由OC=R,设∠COB=θ,则BC=OCsinθ=Rsinθ.
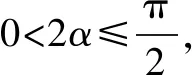
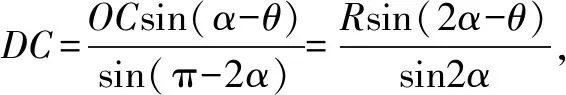
∴只需sinθsin(2α-θ)=sinθsin2αcosθ-sin2θcos2α