一道恒成立问题的三种处理策略
2019-04-04杨苍洲
杨苍洲
(福建省泉州第五中学城东校区 362000)
题目若关于x的不等式x(1+lnx)+2k>kx的解集为A,且A⊆(2,+∞),则整数k的最大值是____.
本题主要考查函数、导数及其应用、不等式等基础知识;考查运算求解能力、推理论证能力等;考查数形结合思想、函数方程思想、化归与转化思想、分类与整合思想等.本题具有一定的难度,是高考模拟题的填空压轴题.
求解本题时,从处理参数的角度看,常见的解题思路有:
(1)分离参数;
(2)半分离参数;
(3)不分离参数.
下面我们分别从这三个角度对本题进行分析与解.
一、分离参数
参数分离是处理恒成立问题的常见策略之一.当题干所给的等式或不等式含有多个变量时,往往通过恒等变形,把参数a与变量x完全分开,分别置于等式或不等式的两边;再把含变量x的一边构造成函数f(x);最后通过研究动直线y=a与曲线y=f(x)的位置关系,从而得到参数a的取值范围.

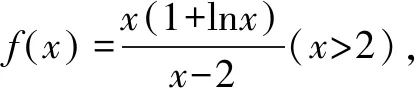

所以g(x)在(2,+∞)单调递增.
又因为g(8)=4-2ln8<0,g(10)=6-2ln10>0,
所以存在t∈(8,10),使得g(t)=0.
且当x∈(0,t)时,g(t)<0,f′(t)<0,f(x)单调递减;当x∈(t,+∞)时,g(t)>0,f′(t)>0,f(x)单调递增.
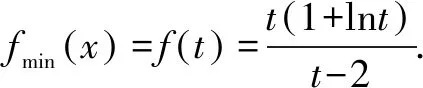
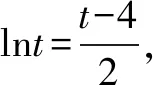
又因为k “化生为熟”是常见的解题方向.我们常常考虑把题干所给式子分解成两个熟悉的函数f(x),g(x),其中f(x)不含参数a,g(x)为过定点的一次函数;然后以导数为工具研究函数f(x)的性质,并作出大致图象;最后通过研究动直线的运动情况,寻找满足条件的动直线,进而限制出参数a的取值范围. 解法二由x(1+lnx)+2k>kx,得x(1+lnx)>k(x-2). 令f(x)=x(1+lnx)(x>2),则f′(x)=lnx+2>0. 所以f(x)在(2,+∞)单调递增. f(x)的图象大致如图: 整理得,ek0-2-2k0=0(*),其中k0>2+ln2. 令g(x)=ex-2-2x(x>2+ln2),则g′(x)=ex-2-2>0. 所以g(x)在(2+ln2,+∞)单调递增. 又因为g(4)=e2-8<0,g(5)=e3-10>0,所以方程(*)存在唯一解k0,且k0∈(4,5). 由图可知k 当分离参数使得问题变得更加复杂时,我们往往考虑带参讨论.首先需要构造含参数a的函数f(x),然后对参数a的不同取值进行讨论,并研究所对应的动曲线y=f(x)的不同性态,从中寻找满足题意的曲线,从而得到参数a的取值范围. 解法三由x(1+lnx)+2k>kx,得x(1+lnx)+2k-kx>0. (1)当k≤1时,f′(x)>0,f(x)在(2,+∞)单调递增,f(x)>f(2)=1+ln2>0,满足题意; (2)当k>1时,由f′(x)=0,得x=2k. 当x>2k时,f′(x)>0,f(x)单调递增;当2 故fmin(x)=f(2k)=ln(2k)+2-k,所以ln(2k)+2-k>0(*). 又因为g(4)=ln8-2>0,g(5)=ln10-3<0,故存在t∈(4,5),使得g(t)=0. 所以不等式(*)的解集为(2,t),其中t∈(4,5). 综上述,k 又因为k∈Z,所以k的最大值为4.二、半分离参数

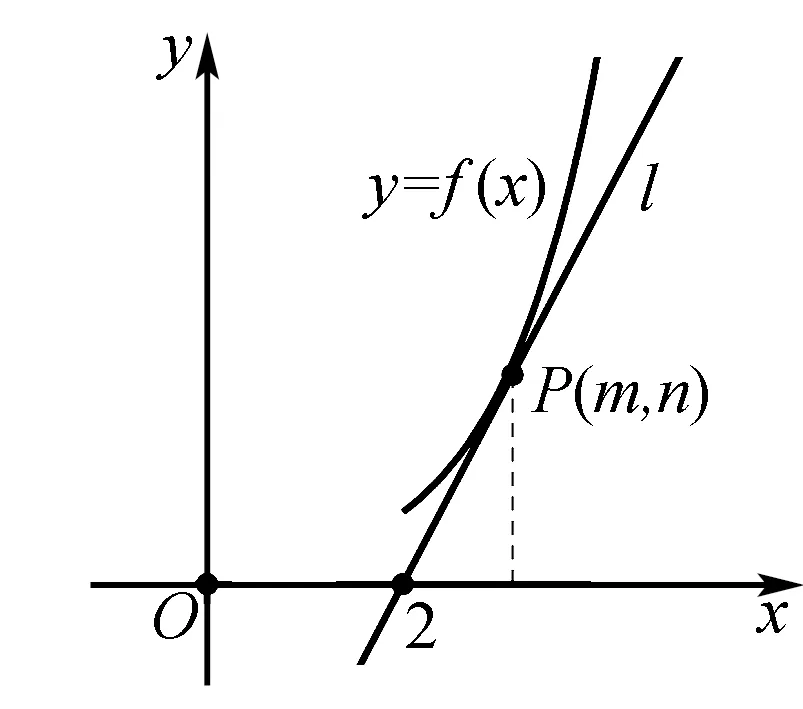

三、不分离参数