圆锥曲线离心率 几何坐标思定义

陆勇平

(福建省泉州外国语学校 362000)

一、涉及焦点及曲线上的点问题，几何坐标思定义(想方程)

解法1 如图所示，设椭圆的另一个焦点为F1，连结AF1.

∵△AOF2为正三角形, 设|F1F2|=2c>0,

∴|OF1|=|OF2|=|OA|,

由椭圆定义得|AF1|+|AF2|=2a,

解法2 设|F1F2|=2c>0,

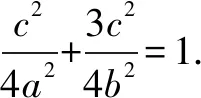
又∵b2=a2-c2,

∴c4-8a2c2+4a4=0.

同除以a4可得e4-8e2+4=0,

点评解法1利用圆锥曲线的定义求解，同时渗透平面几何知识是求圆锥曲线的离心率的常用方法，应优先考虑该方法.解法2利用点在曲线上得到a,c的齐次方程，再同时除以a4,转化为关于离心率e的方程，从而求出e，这种方法是求解离心率的本质，但计算量较大.

二、涉及到两焦点或到长轴两端点张角问题，熟记定论并用几何法巧解

∴3c4+4a2c2-4a2≥0，即3e4+4e2-4≥0,

解法2 同解法1可证当点P位于短轴端点时，∠APB最大.

∴a2≥3b2,即a2≥3(a2-c2),

解法1 设|PF1|=m,|PF2|=n(m>0,n>0),

由余弦定理可得4c2=m2+n2-2mncos120°=m2+n2+mn即4c2=(m+n)2-mn,∴4c2=4a2-mn,

解法2 设|PF1|=m,|PF2|=n(m>0,n>0),

由余弦定理及椭圆定义可得

当且仅当m=n时等号成立，此时cos∠F1PF2取最小值， ∠F1PF2最大，点P在短轴端点.

∴c2≥3b2即c2≥3(a2-c2),

三、涉及中位线问题时，巧用几何法结合定义

解法1 如图， 设F1为双曲线的右焦点，P为双曲线第一象限上的点.

∵M为线段PF2的中点，O为F1F2中点，且|OF2|=|F2M|=c，|PF2|=|F1F2|=2c.

由双曲线的定义可知|PF1|=|PF2|+2a=2a+2c.

OM为△PF1F2的中位线，∴OM∥PF1，

点评解法1利用等腰三角形(或余弦定理)确定三角形各边的关系，再巧妙利用双曲线的定义构建a,c的关系，这是离心率求值的常用方法.解法2设出点P的坐标后代入双曲线方程，构建a,c的关系去求离心率的值，这种方程思想在解题中经常用到，但计算量较大.解法3结合双曲线的定义，巧妙地利用正弦定理把各边的比转化为各角的正弦值的比，这种方法更加简捷.

四、涉及圆锥曲线中的向量问题，巧设坐标思定义

解法1 如图，取PF2中点M，连接OM.

又∵O,M分别是F1F2,PF2的中点,∴OM∥PF2，∴PF1⊥PF2,∴△PF1F2为直角三角形.

设|PF1|=4k,|PF1|=3k(k>0),

∴|F1F2|=5k.

∴△PF1F2为直角三角形，PF1⊥PF2.

接下来同解法1可得e=5.

评点解法1利用向量的线性运算得出△PF1F2为直角三角形，再结合双曲线的定义，巧妙地利用正弦定理把各边的比转化为各角的正弦值的比，这种方法简捷、灵活.解法2利用向量的线性运算,把向量用相同的基表示，得出△PF1F2为直角三角形.

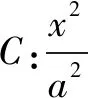
又∵点P在椭圆上

又∵P为椭圆上一点,∴b2≤3c2≤a2.

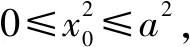
解法1将数量积用坐标表示后转化为圆的方程的形式，巧用圆与椭圆交点结论求解，把向量问题转化为不等式问题，对学生综合分析问题的能力要求较高.解法2利用向量的线性运算把向量用相同的基表示，得出椭圆上点到原点的距离，再利用距离的有界得出不等式，这是处理离心率范围问题的常用方法.解法3将数量积用坐标表示后转化为有关横坐标x0的关系式，并利用x0的有界性求解，对学生的综合分析能力和运算能力要求都较高.