密立根油滴实验数据处理的多重差值法

宋元军

(河北北方学院 理学院，河北 张家口 075000)

密立根油滴实验[1]作为近代物理实验中的典型实验，不仅可以让学生切身体会到测量微观物理量的巧妙设计思想，而且多种可供选择的测量方法也是培养学生创新思维的重要素材． 密立根油滴实验还有许多数据处理方法，从使用的数学工具角度来说，有简单代数法[2-4]、函数法[5]、统计处理方法[6-7]、几何作图法等[8]． 目前，高校实验室的油滴实验设备多数配有CCD成像系统，相比传统的显微观测系统，测量起来比较容易，这就为在实验课堂上收集容量较大油滴电量样本提供了可能，也为学生尝试用多种方法处理实验数据奠定了基础． 本文研究了密立根油滴实验数据处理的简单代数方法中的油滴电量逐项相减法，将针对其缺点，尝试对其进行改进．

1 多重差值法

1.1 多重差值法的基本思路

油滴电量逐项相减法把样本电量从小到大排序，相邻的大序号电量减去小序号电量，然后对差值进行分析，从而得到基本电荷电量估计值． 该方法处理油滴实验数据，容易得出电荷的不连续性，得到的基本电荷电量的估计值一般会偏小[2]． 文献[2]给出了改进方法——油滴电量平均值逐项相减法． 油滴电量平均值逐项相减法在油滴电量逐项相减法的样本电量排序、依次作差的基础上，按照油滴带基本电荷个数多少对油滴电量进行分类，并对各类的平均值再次实施逐项相减法． 但油滴电量平均值逐项相减法也存在不足，即在样本中各个油滴带基本电荷个数连续分布情况下，基本电荷电量的估计值只受带基本电荷个数最多的油滴电量和带基本电荷个数最少的油滴电量的影响，而不受带基本电荷个数为其他值的油滴电量测量值影响． 本文对油滴电量逐项相减法的改进思路是：把相邻作差改为多重作差，即不仅相邻作差，不相邻也要作差，然后把所有差值进行分类，最后把对应1个基本电荷的一类差值求平均得到基本电荷电量估计值．

1.2 多重差值法处理实验数据步骤

首先，把实验测得的油滴电量从小到大排序． 其次，选取序号间距为1，油滴电量依次作差． 分析作差得到的数据分布情况，把所有差值分为3类：小值类、中值类和大值类． 然后，把作差对应的序号间距增加1，再依次作差；把作差对应的序号间距增加2，再依次作差；以此类推……直到小值类差值不出现，且中值类差值只有1个或不出现时，作差计算结束． 最后，把属于中值类的差值求平均，得到基本电荷电量的估计值．

1.3 数据处理举例

整个作差过程如表1所示． 表1中i为油滴电量从小到大排序后的油滴序号，Qi为第i个油滴的带电量，ΔQj=Qi+j-Qi为油滴序号间距为j时的油滴电量依次相减所得的差值．

表1 样本a的多重作差数据表 (10-19 C)

从表1可看出，ΔQ1列的差值可以分为3类：第1类为小值，包括0.02×10-19，0.04×10-19，0.01×10-19，0.00，0.19×10-19C；第2类为中值，包括1.53×10-19，1.49×10-19，1.50×10-19C；第3类为大值，为3.11×10-19C． 考虑到误差因素和带电量相邻油滴可能带基本电荷数之差大于1的情况，显然第2类差值对应着相差1个基本电荷电量的情况． 需指出的是，给其他各列差值分类时应注意：后1列每类差值中的最小值一定大于前1列对应类别的最小值． 通过上述分析，容易看出多重作差后得到的中值类差值有1.53×10-19，1.49×10-19，1.50×10-19，1.55×10-19，1.51×10-19，1.53×10-19，1.69×10-19，1.55×10-19，1.54×10-19，1.69×10-19，1.56×10-19，1.54×10-19，1.70×10-19，1.56×10-19，1.73×10-19，1.74×10-19，1.75×10-19C，取平均值后得1.60×10-19C，此值已非常接近基本电荷电量的公认值1.602×10-19C． 从表1也容易看出，ΔQ1列中第2类差值的最大值为1.53×10-19C，因而，油滴电量逐项相减法得到的基本电荷电量估计值为1.53×10-19C． 此值与基本电荷电量公认值的相对偏差为4.5%． 可见，采用多重差值法可以明显改善油滴电量逐项相减法处理数据结果偏小的不足.

样本a是在实验室利用学生实验设备——南京培中MOD-5型油滴仪测得的样本． 选用文献[2]中的样本(简称样本b)作为处理对象． 利用多重差值法对样本b的处理过程见表2．

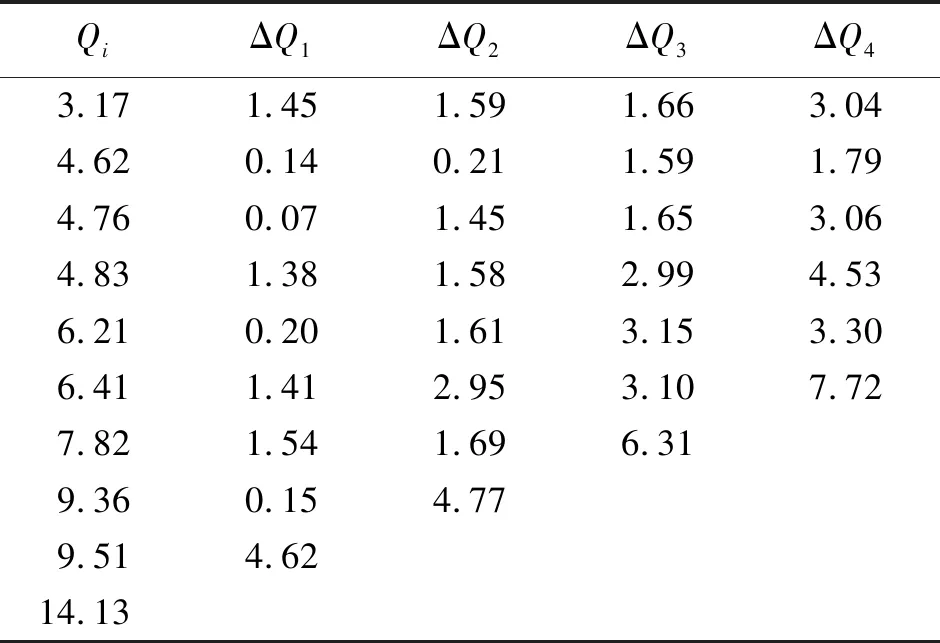
表2 样本b的多重作差数据表 (10-19 C)

从表2第2列可以看出，由油滴电量逐项相减法得到的基本电荷电量的估计值为1.54×10-19C，利用多重差值法得到的估计值为1.57×10-19C． 多重差值法的处理结果明显优于油滴电量逐项相减法的处理结果. 文献[2]中，根据油滴电量平均值逐项相减法处理上述样本得到的基本电荷电量估计值为1.57×10-19C． 尽管多重差值法和油滴电量平均值逐项相减法的处理结果基本相同，但利用多重差值法处理该样本，1，2～6，8～9这8个油滴电量任一变化都要影响估计值，而利用油滴电量平均值逐项相减法处理该样本，只有1，8和9这3个油滴电量变化影响估计值． 由此可见，多重差值法比油滴电量平均值逐项相减法更具有科学性.

2 对多重差值法的几点分析

表1和表2中的样本具有共同特点，就是样本中多次出现带某种数目基本电荷的油滴． 这样的油滴在样本中出现的次数越多，作差的层次就越多，处理结果一般也会更好． 显然，使多重作差法发挥优点的前提是，带某种数目基本电荷(或某几种数目基本电荷)的油滴重复出现． 由于操作者选择某种参量的油滴的倾向性，这种特点的样本在实际实验中比较容易得到． 当样本中不同油滴带基本电荷数全部不同时，多重差值法回归到油滴电量逐项相减法．

考虑到测量误差，样本中带电荷最多的油滴带基本电荷个数7个以上时，组内作差(带基本电荷个数相同的不同油滴电量之间的作差)和组间作差(带基本电荷个数相差为1的2个油滴电量之间的作差)得到的2类差值大小的区分有可能会不明显． 所以，样本中每个油滴带基本电荷个数一般不能太多． 实际实验中，可以通过控制平衡电压和下落时间的取值范围来达到上述要求． 另外，油滴带基本电荷数目种类要丰富(3种以上)． 为此，可以选择平衡电压和下落时间不同的油滴进行测量．

鉴于上述分析，样本容量不能太小，同时为了作差简单，一般情况下，样本容量可取10． 除此之外，油滴电量测量误差越小，多重差值法处理结果也会越好．

3 结束语

运用多层次作差和求平均的思想，给出了多重差值法． 多重差值法既保留了油滴电量逐项相减法简单直观且易于得到电荷不连续性的优点，又克服了其一般情况下得到的基本电荷电量测量值偏小的缺点，还具有估计值敏感依赖于样本中绝大多数油滴电量值的科学性． 用多重差值法对不同样本进行处理，得到较好的结果． 这种方法丰富了密立根油滴实验的数据处理方法的种类． 在对实验室仪器误差进行准确评价测定的基础上，适当控制实验条件(控制平衡电压和下落时间)，多重差值法在密立根油滴实验教学中有应用参考价值．