对基于激光单缝衍射测量实验的优化

李 俊,莫绪涛,黄仙山

(1.安徽工业大学 数理科学与工程学院，安徽 马鞍山 243032； 2.同济大学 物理科学与工程学院，上海 200092)

自1960年梅曼发明激光器以来，激光的应用日益广泛. 由于激光具有单色性好和亮度高等优点，经常被用作干涉和衍射实验的光源. 在直接使用高斯光束作为夫琅禾费衍射光源时，理论分析表明其衍射光斑分布与均匀光的夫琅禾费衍射光斑分布存在一定偏离[1-3]. 其原因在于高斯光束的光强分布不均匀，即在衍射平面上的光强中间强两侧弱. 单模激光除了具有与高斯光束相类似的光强分布外，在衍射平面上的相位也不相等. 当以均匀光作为夫琅禾费单缝衍射光的光源时，可以根据衍射反比关系即可反推缝宽大小. 目前，利用单缝衍射对狭缝尺寸进行测量在实验和工业中都有着普遍的应用[4-6]. 如果以基模激光作为衍射光源对狭缝进行测量，则需要在实验和算法等方面做相应改进. 文献[7]中已经提出精确测算激光单缝衍射实验中缝宽大小的计算机算法. 本文依据基尔霍夫衍射理论，从理论上分析了误差产生的主要原因，结合实验改进，实现了对亚毫米尺寸的精确测量.

1 理 论

基模激光复振幅的空间分布关系为[8]

(1)

式中

(2)

(3)

其中，ω0为激光束腰斑半径，z0为距束腰斑的距离，λ为激光的波长.ω0和z0可以利用文献[9]的方法测得. 由(2)式可以看出ω和z0满足双曲函数关系，即激光半径沿激光传播方向是双曲线分布.

设狭缝宽度为2a，缝与接收屏的距离为D，基模激光束垂直于狭缝平面入射且其光束中心通过单缝中心，则当系统满足远场条件D≫(2a)2/λ时，仅考虑一维情况，可由菲涅耳-基尔霍夫衍射积分公式给出接收屏上任一点的复振幅为[10]

(4)

则光强大小分布为

I(x′)=|U(x′)|2.

(5)

由于(4)式的积分比较复杂，无法直接求出解析解，为此通过数值方法处理上述积分计算.

以上分析可以看出基模激光与均匀光的区别主要在于激光光束的光强和相位的不均匀性，而相位的不均匀性主要取决于激光器的束腰半径大小和衍射屏与激光器束腰之间的间距. 为了区分光强和相位对单缝衍射的影响，首先计算了等相位的高斯光束的衍射光强分布，如图1所示. 从图1可以看出高斯光束的衍射光强分布相对于均匀光存在着向两侧的偏移，且随着缝宽和激光光斑直径比值(a：ω，简称比值)不断增大，1级暗纹和1级亮纹位置的偏移量随之逐渐增大，1级光的光强与0级光的比值明显降低.

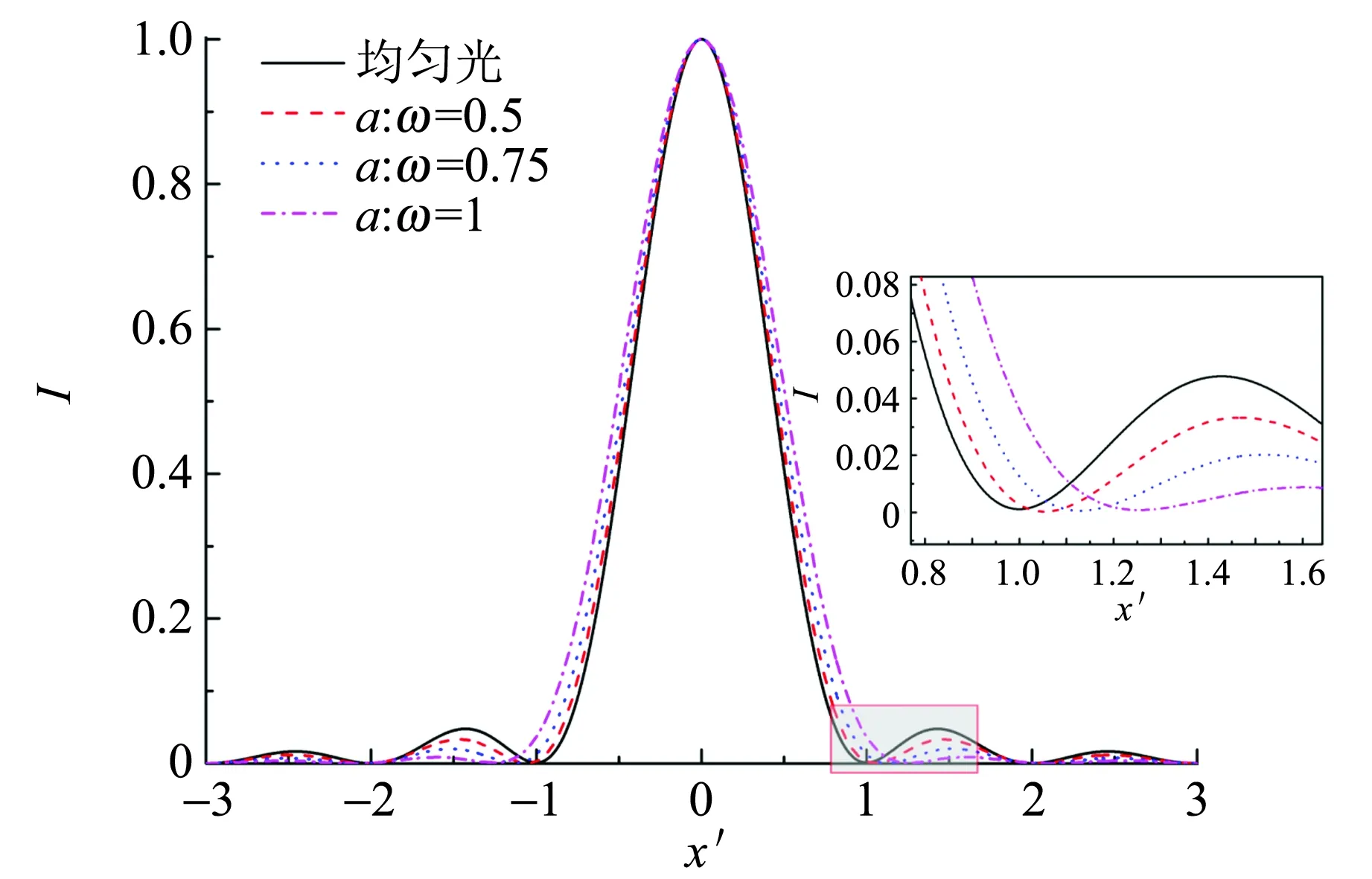
图1 均匀光与不同比值的高斯光束单缝衍射分布图

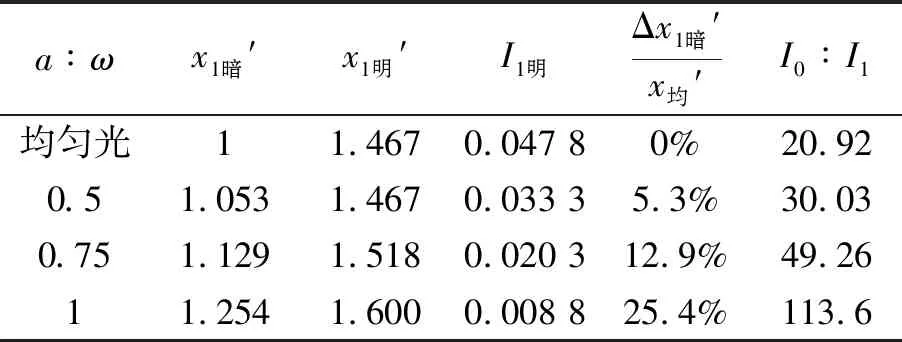
表1 均匀光与不同比值的高斯光单缝衍射参数对比

图2是考虑了振幅和相位的不均匀性即实际基模激光与均匀光单缝衍射光强分布对比图. 设定激光器的束腰半径为0.1 mm，衍射屏距激光束腰的距离为80 mm. 与图1相比，其偏移程度随比值的增大明显增加，且1级暗纹光强并不为0，存在一定的亮度. 当比值大到一定程度1级暗纹消失，0级亮纹与1级光重合. 此时，无法利用激光单缝衍射的方法测量相对较宽的狭缝.

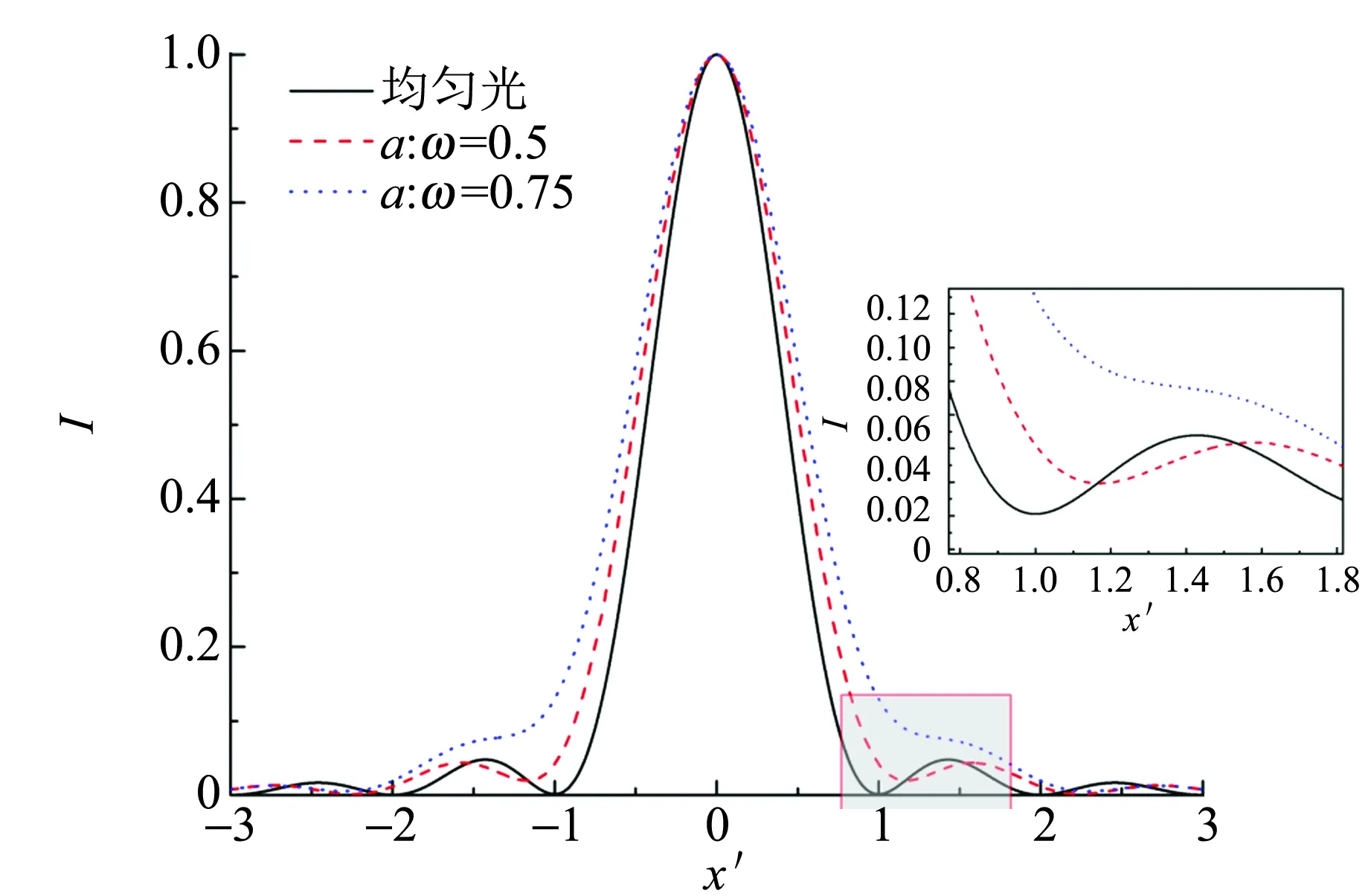
图2 均匀光与不同比值的基模激光单缝衍射分布图

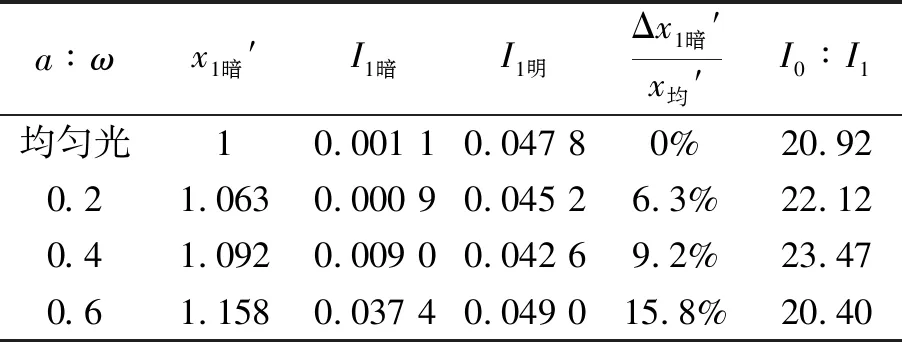
a∶ωx1暗′I1暗I1明Δx1暗′x均′I0∶I1均匀光10.001 10.047 80%20.920.21.0630.000 90.045 26.3%22.120.41.0920.009 00.042 69.2%23.470.61.1580.037 40.049 015.8%20.40

在激光实验中，经常需要使用透镜将激光按照要求匹配进入到激光处理器件中. 激光在经过透镜时，存在以下规律[8]：

(6)

(6)式中，F为透镜焦距，ω0为激光的束腰斑半径，l为激光束腰斑到透镜焦平面的距离，则ω0′为激光经过透镜后的束腰斑半径，l′为激光经过透镜后束腰斑到透镜焦平面的距离.

根据以上规律，设计了图3所示的双透镜结构来降低因高斯光束光强和相位分布的不均对单缝衍射造成的误差.

如图3所示，激光从左边入射，经过第1个透镜后，会产生新的双曲线分布，适当调节第1个透镜的焦距和与激光器束腰的距离，可以实现扩束效果. 再经过第2个透镜又会产生新的双曲线分布. 现将狭缝置于第2个透镜的左边附近，即让激光经过第1个透镜扩束后再通过狭缝，以降低比值大小，从而减小激光分布不均匀带来的影响. 再将接收光屏置于第2个透镜的右方束腰位置处，即等相位面位置，以排除相位分布不均匀的影响. 因此，通过以上透镜系统，即可很好地从实验上解决因光强和相位的不均匀而带来的影响.

图3 基模激光光束经过透镜变换示意图

为了从理论上验证扩束后的光束对于衍射光斑平移量的改进，取ω=10a的情况进行计算比较，得出1级暗纹归一化的位置为1.002，相对于均匀光的偏移比仅为0.2%. 由此可以看出，通过增加缝宽和激光光斑半径的比值，可以明显降低因激光能量分布不均匀带来的误差.

2 实 验

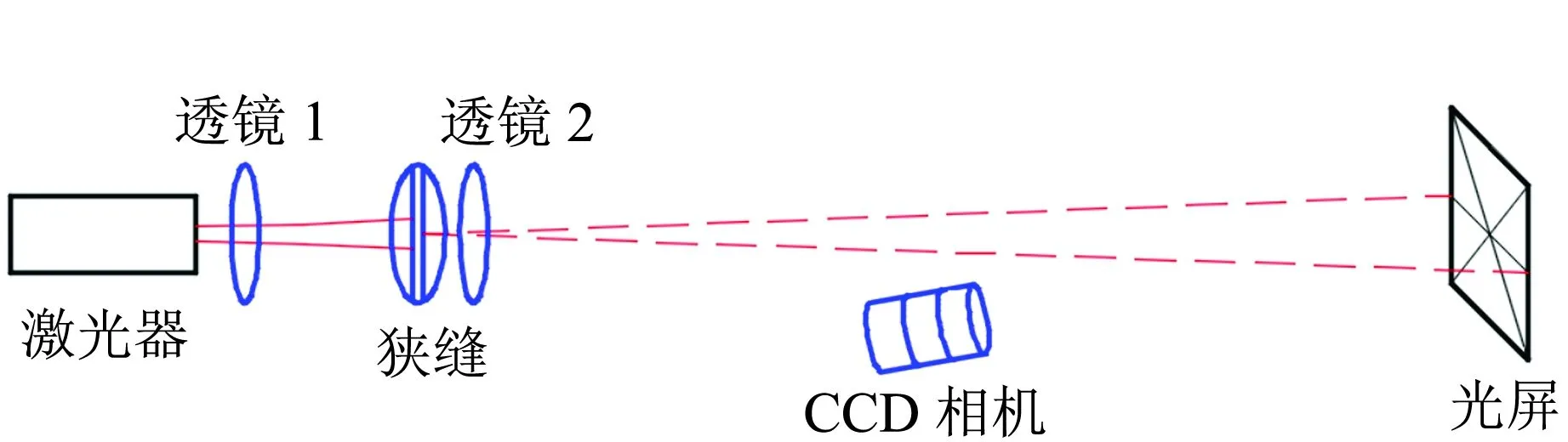
图4 激光单缝衍射测量狭缝宽度实验示意图

通过以上理论分析，设计出激光单缝衍射测量狭缝宽度实验示意图如图4所示. 其中，激光器采用532 nm的普通半导体激光器，狭缝采用螺旋式宽度可变的刀口，根据(6)式和(2)式可知，为了在狭缝处获得较大光斑(较小的束腰半径)，第1个透镜应尽量取短焦距. 为了具有较大的衍射间距，第2个透镜应取较长焦距，故采用2个焦距分别为15 mm和250 mm的正透镜，CCD相机是型号为MER-500-7UM的大恒黑白相机.

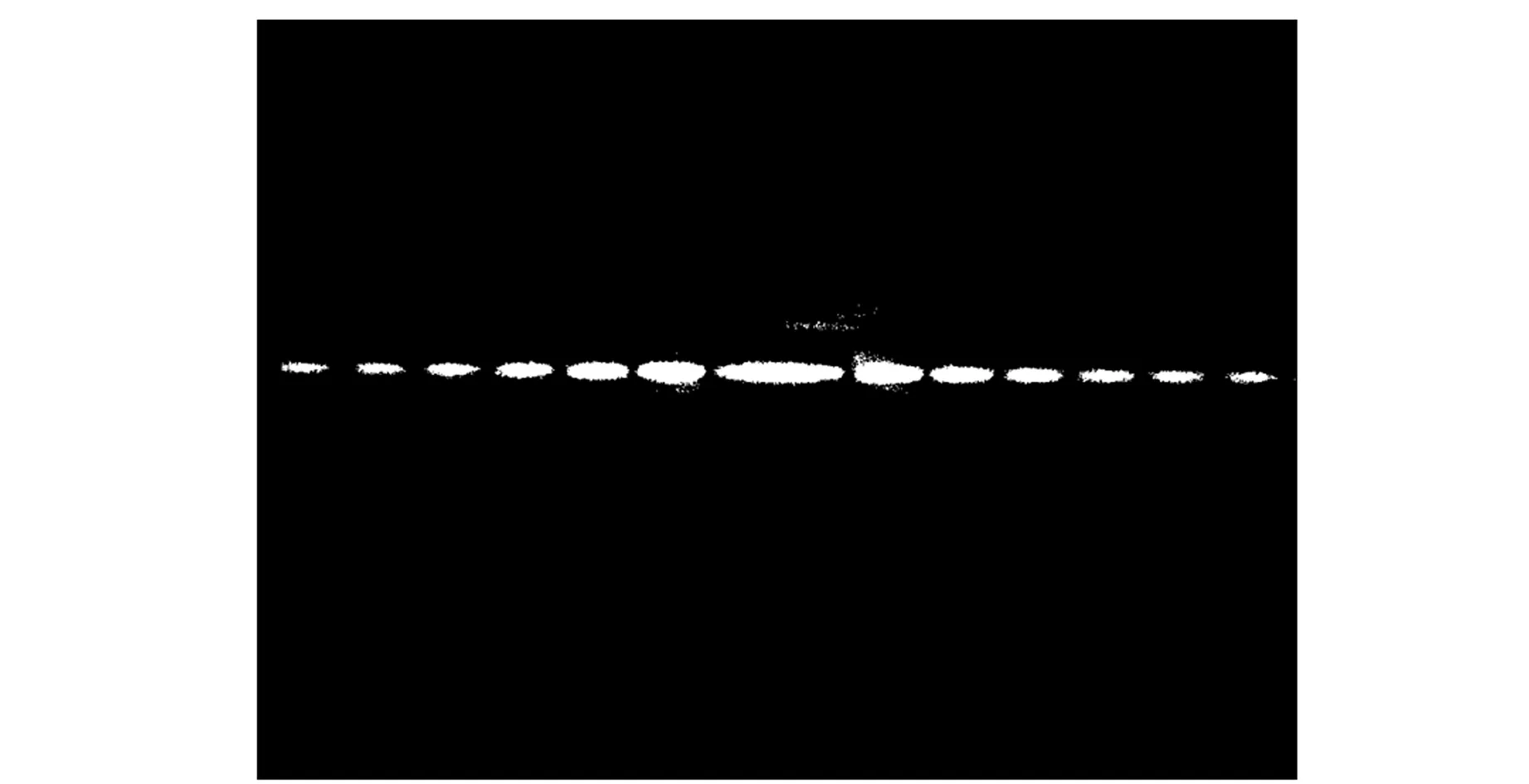
首先测定激光器的束腰大小和位置，根据(6)式计算并设定2个透镜和光屏的位置,设定衍射屏到光屏的为2 000 mm，螺旋刀口设定的狭缝宽度为0.42 mm. 根据相应的参数按图4搭建实验平台，用CCD相机拍摄光屏上的光斑分布如图5所示. 再保持各器件在原来位置，拿走2个透镜并适当调节光圈大小后拍摄的光斑分布如图6所示. 由于衍射光斑中间强两边弱，故在光屏上将0级光处涂成黑色以吸收部分光，降低其与其他级衍射光斑的对比度，防止中间光斑光强过强CCD拍摄无法分清. 图5下部分是普通直尺，用于标定CCD相机拍摄图片尺寸的放大率. 将图5和图6进行对比，可以清晰地看出，在衍射光路中拿走双透镜系统后，0级与其他级次地光强对比度明显提高，且中心明纹变宽，即1级暗纹位置向两边平移，这些与前的理论计算结果是一致的.

图5 CCD相机拍摄的衍射光斑分布图

图6 移除透镜时CCD相机拍摄的衍射光斑分布图

(a)较大阈值下的二值化后衍射光斑分布图

(b)较小阈值下的二值化后直尺刻度分布图图7 不同阈值的二值化后的分布图

对图5进行2次二值化处理如图7所示. 图7(a)为较大阈值下的衍射光斑分布图，图中只有黑色背景和白色光斑，可以很好地算出光斑分布情况. 图7(b)是较小阈值下的二值化处理后的图像，图中直尺刻度清晰，可以利用程序计算出刻度间的像素数，进而求出CCD相机的放大率.

根据相关测量参量的不确定度及运用单缝衍射反比关系，计算出缝宽为0.421 mm，与所设定的狭缝宽度接近，且根据参量的不确定度[11]进行误差分析，理论上精度可达μm量级. 由此可见，使用这种方法进行的亚毫米级尺寸测量是可行的.

3 结束语

在光路中使用2个透镜后，可以很好地降低因单模激光在衍射屏上光强和相位的不均性而引起的衍射光斑平移，进而实现与均匀光近似相同的衍射分布. 因此，可以利用衍射反比关系，实现对亚毫米级狭缝宽度或细丝直径等物体尺寸的非接触式光学精确测量.