扭转陀螺运动系统的研究

陈宗强，于宏宇，陈 靖,孙 骞

(南开大学 物理科学学院，天津 300071)

扭转陀螺为第30届国际青年物理学家竞赛(IYPT)第12题[1]，使用1根具有一定扭转阻力的绳来悬挂转动的陀螺，加速陀螺使其具有一定的初始自转角速度，并且将绳扭转一定的角度，然后释放，陀螺会进动、章动运动，由于陀螺质心与轮轴存在的无法避免的微小偏移，陀螺会进行参变共振与受迫共振. 在一定情况下，陀螺会发生进动与章动[2-3]、共振现象[4]. 本文将从陀螺轮轴自转角速度变化、绳扭转提供的力矩随时间推移变化等分析扭转陀螺运动系统的角动量以及外力矩的具体形式，对角动量定理的复杂方程数值求解，并且与实验比较，对进动、章动以及共振分析内在的原因. 此外，从陀螺偏心差的角度对章动、参变共振与受迫共振进行理论以及实验的解释与探究.

1 理论分析

1.1 模型建立

如图1所示，假设绳固定点为O，系统静止时轮轴朝向为x轴正方向，重力加速度方向为z轴正方向，根据右手螺旋确定y轴正方向，A为轮与绳固定连接点，B为陀螺的质心位置，绳长OA为a，陀螺质心B与绳和轮连接点A距离为b.

由于绳的伸缩量在运动过程中近似不变，故OA大小不变，具有2个自由度，包括绳与竖直方向夹角θ和扭转角度β. 轮自转角度具有1个自由度，由于OA与AB近似处于同一平面内，故具有轮轴与水平平面夹角自由度φ.

图1 扭转陀螺运动模型

1.2 系统角动量

系统角动量由质心角动量与质心系中角动量组成. 质心角动量可以表示为

(1)

其中

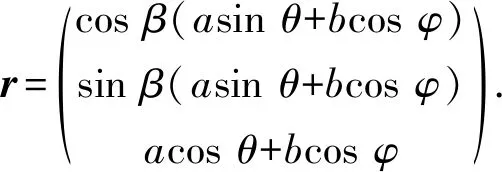
对质心系中角动量进行分析，质心系中的角动量由3部分组成：第1部分J1为陀螺绕自陀螺轴旋转所获得的角动量，第2部分J2为φ变化所获得的角动量，第3部分J3为β变化获得的角动量. 故陀螺系统角动量J为

J=J0+J1+J2+J3=

(2)

其中，I1，I2和I3分别为陀螺对应轴的转动惯量；ω为陀螺自转角速度，会随时间推移而减少.

1.3 外力矩

系统所受外力矩由2部分组成：第1部分为重力矩Mg，第2部分为绳扭转提供的扭转力矩Ms，其中

(3)

通过分析绳扭转内在变化分析Ms. 绳扭转过程内部发生形变，从而产生恢复力矩，力矩大小与绳材料的剪切模量以及横截面有关，同时扭转过程绳内部存在摩擦阻力，故绳扭转产生力矩表示为

(4)

故得到系统所受外力矩为

M=Ms+Mg=

(5)

将系统所受外力矩以及角动量对时间微分形式列式即可得到3个包含绳与竖直方向夹角θ、扭转角度β和轮轴与水平平面夹角φ的完整微分方程，结合初始条件

对方程进行数值求解，可以得到θ，β以及φ随时间变化.

2 实验分析

2.1 实验装置

扭转陀螺的实验装置如图2所示. 使用1根具有一定扭转阻力的绳悬挂转动的陀螺，加速陀螺使其具有一定的初始自转角速度，并且将绳扭转一定的角度，然后释放. 实验中，在3个视角观测记录定制轮的运动情况，水平视角放置2台摄像机以获得轮轴与水平平面夹角φ的变化情况，其中1台为高速摄像机慢速观察转动情况，竖直方向放置1台摄像机以获得扭转角度β变化情况. 使用Tracker软件追踪φ和β随时间变化. 用直尺测得绳长a、陀螺质心B与绳和轮连接点A距离为b，用电子天平测得陀螺的质量，用三线摆转动惯量仪测得陀螺的3个轴的转动惯量. 实验中各参量如下:a=294.0 mm，b=44.0 mm，m=0.343 21 kg，g=9.80 m/s2，βt=0=8π，I1=1.377 8×10-4kg·m2，I2=I3=6.428 8×10-5kg·m2.

图2 扭转陀螺的实验装置

为了获得陀螺自转角速度随时间变化情况，先让绳不扭转，轮空转，使用800帧高速摄像机正对其拍摄，获得其角速度ω随时间变化关系，如图3所示. 由图3可以看出，角速度与时间近似成线性关系，故将角速度ω表示为

ω=ω0-k0t,

(6)

拟合得k0=7.295 rad/s2.

图3 陀螺自转角速度与时间关系

保持轮不旋转，只扭转绳，从陀螺底部拍摄获得扭转角度β随时间变化如图4所示，其中β0=-40 rad,dβ/dt=0. 扭转角度β拟合满足

β= -38.4e-0.122t[cos (0.458t)-

0.815sin (0.458t)],

(7)

可得：k1=2.85×10-4,k2=3.10×10-4.

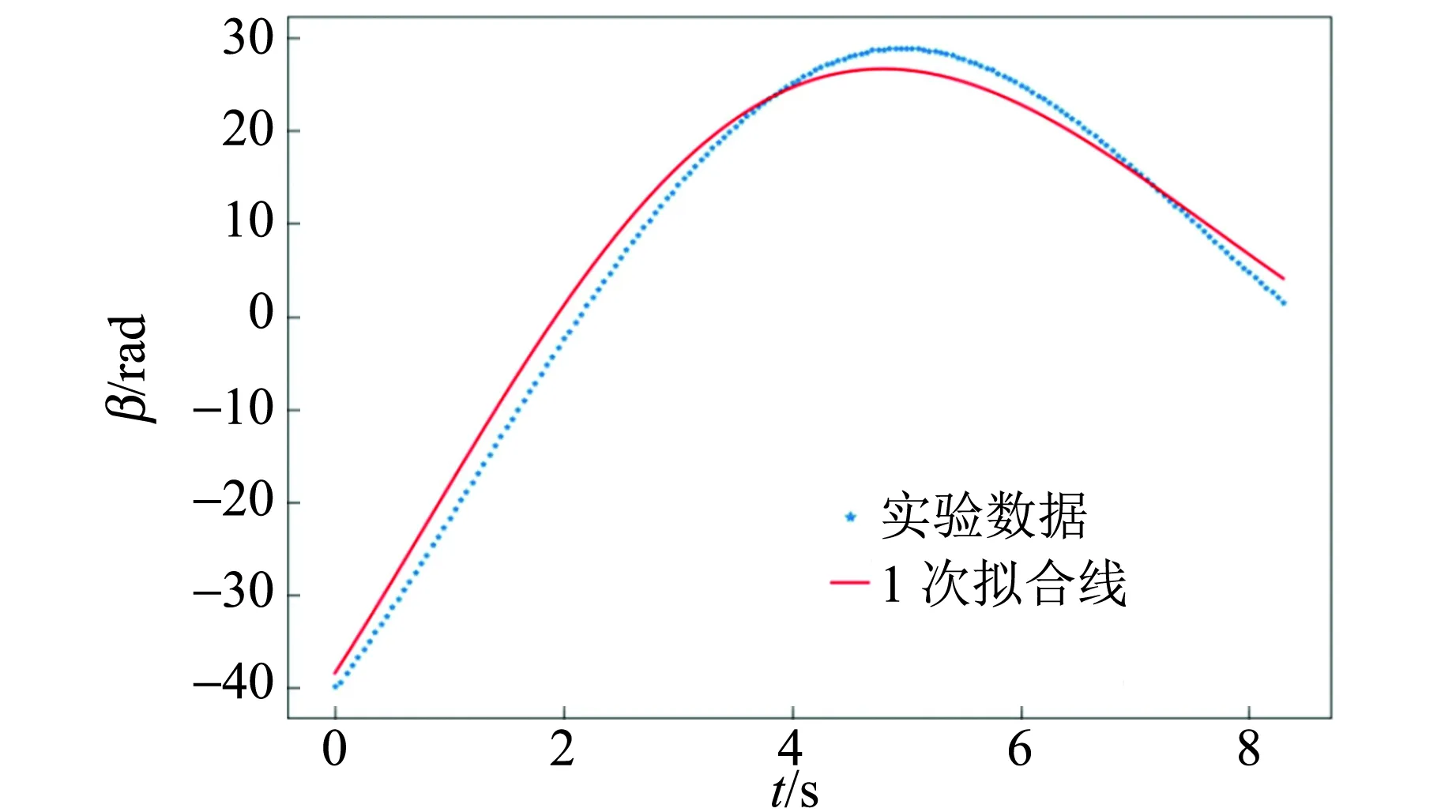
图4 轮不旋转只扭转绳时陀螺扭转角度与时间关系

2.2 实验结果与分析

将理论数值求解所得的扭转角度β与实验获得数据值对比，如图5所示. 由图5可以看出扭转角度随着时间减小，由上方绳提供主要扭转力矩. 与陀螺空转相比陀螺扭转恢复速度明显减慢，这是因为陀螺转动时存在的自转角动量阻止了扭转运动的发生.

图5 轮旋转绳也扭转时陀螺扭转角度随时间变化

将理论数值求解所得的轮轴与水平平面夹角φ与实验获得数据值对比，如图6所示. 由图6可看出，φ先增大再减小，陀螺会出现轮轴抬起与水平平面有夹角的原因主要为轮转动使得轮自转角动量方向变化，损失角动量转换至φ变化的角动量中，而重力矩使φ减小，故φ达到一定值会趋向于减小直至运动停止. 此外，φ实验值在理论值附近波动，进行章动，章动主要由偏心差引起.

图6 陀螺轮轴与水平平面夹角φ随时间变化

3 偏心差的影响

由于陀螺无法保证完全的质量分布均匀，陀螺质心会与轮轴中心存在较小的偏差，该偏差称为偏心差. 在轮旋转时，偏心差会导致陀螺质心绕轴转动，产生向心加速度，从而对运动产生一定影响. 向心加速度所引起的力矩方向沿轮轴与水平平面夹角φ变化角动量方向，故对φ进行相应分析.

当不考虑陀螺偏心差时，φ角运动方程近似写为

(8)

(9)

其中等号左边第2项为阻尼项，第3项为回复项，由常数项及由于质心做圆周运动使得重力矩周期性变化引起，等号右边为向心加速度引起的力矩，x和y分别为质心与轮轴距离、质心在轮轴上投影与轮轴中心偏离距离. (9)式的解可表示为

(10)

时会出现较大波动，即陀螺在转动角速度趋近于ω0会进行受迫共振.

偏心差会引起陀螺进行与轮转动等频率章动，且在转动速度趋近于2ω0与ω0时章动频率较大，分别发生参变共振与受迫共振，其主要使得轮轴与水平平面夹角φ发生波动. 通过高速摄像机进行检验，可以观测到陀螺会进行与陀螺旋转等频率的章动，且观察到在ω=201.12 rad/s与ω=101.05 rad/s章动振幅最大，分别发生参变共振与受迫共振，如图7～8所示.

(a)t=1 s

(b)t=2 s

(a)t=1 s

(b)t=4 s

4 结束语

通过理论与实验分析，得到了陀螺轮转速随时间减慢与轮转动得到陀螺在绳下运动状态，并对运动中轮轴旋转的原因进行了解释. 对偏心差引起的参变共振与受迫共振进行了理论上的分析与实验上的验证. 而由于使用牛顿力学对系统进行分析得到方程式(组)极其复杂，虽然能通过数值求解，但无法较直观地对运动状态进行说明. 本文对解析过程进行了近似，假设绳线性伸长量不变，绳提供的力矩使用了二项阻尼进行拟合，轮转速随时间近似线性变化，且陀螺存在不可避免的偏心差.