探索根源之道 滋润理性之思——以 “分数乘法”为例谈算理与算法处理

王国宏

（浙江省杭州市萧山区江寺小学，浙江 杭州 311201）

新课程标准指出：教学时，应通过解决实际问题进一步培养学生的数感，增进对运算意义的理解。计算教学的目的并不是让学生操练某些习题得到正确的答案，形成某些运算技能，而是让学生在遇到一些数学实际问题，能提出解决问题的方案，当需要计算时，因为对运算意义的充分理解，才能选择合适的算法，并能在算理和算法的提炼归纳中，发展学生的认知能力和思维能力，感悟数学思想方法。

算理是指“为什么要这样计算”的道理，算法就是“怎样来计算”的方法和程序。算理与算法是相辅相成的。然而有很多情况下，学生只知算法而不明算理，甚至有很多情况下，学生通过培训班或者提前学习后，已经懂得算法，并能简单计算，却不太清楚算理。以《分数乘法的教学》为例，笔者在教学之前抽取本校六年级六（1）和六（2）班78人做了前测，前测共3道题，①计算②写法则③说说为什么这么算，并对数据进行了整理和分析。

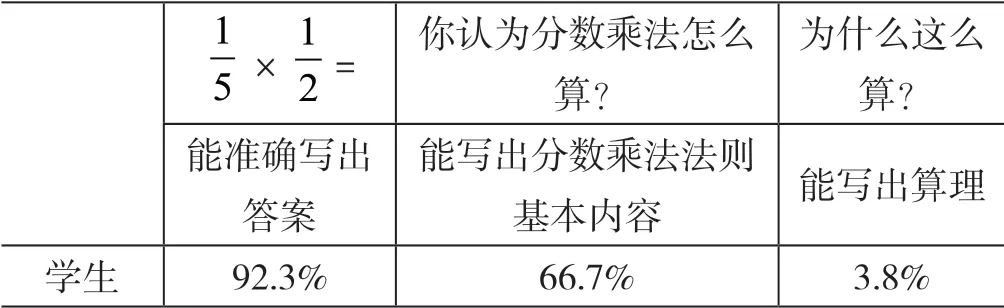
表一：《分数乘法计算法则》前测

表中的数据，关于计算，因为比较简单，因为教材早已下发的原因，学生稍微看书预习一下，也能写出答案，所以新课还没学，很多学生已经会计算了，而且相当一部分学生能写出分数乘法法则的基本内容，而第三个问题“你为什么这么算的依据”，有65%的学生答了“因为简单、方便”，有30%的学生答“规定要这么算的”“规定要这么算的”，只有3位学生用图示画了自己这样做的根据。

基于前测，我们发现，孩子们已经对算法大致了解，但对算理极其不清，而且学生自我感觉，能对算法法则进行简单模仿，机械套用就自认为已经学会了。

一、教学前，对算理分析思考

（一）思考一，为什么学生不重视算理？

对学生而言，初学某个领域的计算，最想知道的是“怎么算”，因为“会算”就意味着就能做对习题、熟练了就能应对考试。因为考试基本上不会考算理，“算理”是个什么东西？平时用不上，所以不重视。同时就成年人而言，某一个领域的计算，当他已经会算了，形成技能了，他还会、还有必要记得“为什么这么算”的算理吗？无需。生活中，常用的是技能而不是算理。所以很多学生学习算法知识技能层面较多，而对思维的方式的正确性，计算中的推导等能力不太重视。

（二）思考二：学生会算了“还要去明晰算理吗”

基于前测，当93%的学生能算出得数，我们“还要去明晰算理吗”？我们思考，学生“会”了什么？如果仅是会算就是“会”了，那么现代社会“计算器”“计算机”又快又熟练，何苦为难孩子？很显然，我们并不要把孩子操练成“计算器”。很显然，计算教学是一个载体，通过计算教学，让学生经历“为什么是这样算”的发现过程，理解“计算方法”源自哪里？这期间所需要的观察、比较、推理、判断、概括、归纳等能力的培养是不言而喻的，所积累的数学活动经验和数学思想方法对孩子发现问题解决问题的能力提升，有了厚积薄发的过程。简单记忆“分数乘分数”计算法则进行操练，与建构在“理解算理基础上的计算方法归纳”，其潜能和思考能力发展是两个完全不同的层次，探索根源之道，才能滋养理性之思。

二、如何引导学生探究“算法”背后的“算理”？

（一）任务驱动，证明猜测，激励学生探求算法依据

当接触一种新的计算法则时，学生已经能简单计算，就要驱动学生思考，利用原有知识储备，思考为什么可以这样算。所以课伊始，安排分数单位相乘的计算。

基于前测，站在学生的学习起点上，当学生得出计算结果时，教师并不作对错判断，而是让孩子想办法证明自己的想法是对的，重心已经从算法转移到算理。

孩子们其实不习惯于表达算理，回答“为什么这样算”是对的，有学生就说“我们培训班老师说过”，有学生说“书上就是这么写的，我看到过的”来回答。老师告知学生“培训班老师说的”，“书上说写的”，都说明古人通过很多次探究在积累，难道我们不会探究吗？说明自己的想法，有根有据地让别人认同你的想法是非常了不起的能力。不唯书、不唯师，是独立思考能力和科学精神的重要表征。

“证明”这一任务的驱动，逼使孩子们由单纯追求计算结果，转移到证明“为什么这么算”，由算法到算理，实际是一个理性思考，需要孩子们去追本溯源，去思考各表示什么意义，小组分享与交流，又利于引发学生多角度发现，算理可以用图、文字、算式等不同的方式进行表述，把思维过程外显，其实是理性思维培养的样式。在思考活动后，学生需把智慧外显，用图、文、算式等不同的方式表达出来。用“证明自己的想法与算法，并向他人分享”这样的核心问题驱动课堂，既促进学生开展深入的思考，又提升学生有理有据地进行表达的能力，同时也能让算理在独立思考的基础上更多样化的表征。

（二）辨析沟通，多样化表征，让学生明确算法依托

研究证明，单纯的行为参与方式并不能促进学生高层次能力的发展，只有以积极的情感体验和深层次的思考为核心的学习方式，才能促进学生的主体发展。学生探究并解释的过程，首先是独立思考，由于有了积极的情感体验和深层次的思考，在小组交流时，学生已经不满足与简单的参与，而是重点在“让同学明白我这样的算法是有根据的”，“教懂别人”，已经是更高层次的学习方式了。所以经过小组交流“求同存异”形成观点，在班级汇报的受一共出现好多方法：

1.意义入手，数形结合，图式化诠释算理

已有认知基础是现实起点，当遇到分数乘分数的算法根据时，学生不知道，自然而然地用“分数的意义”来解释，这说明学生能根据已有的知识经验来解决新的问题，这是认识世界的重要手段，而分数的意义，学生是能够用图来表征的，但是当学生能把自己的思考过程用图画“外显”，这是极好的一种方法。

下面图1，2，3，4是教学实践中，学生对乘法结果的解释与证明：

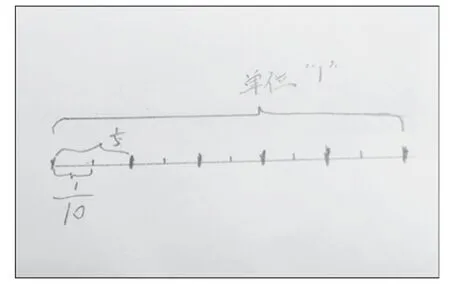
图：1用线段图表示

图2：用长方形图表示

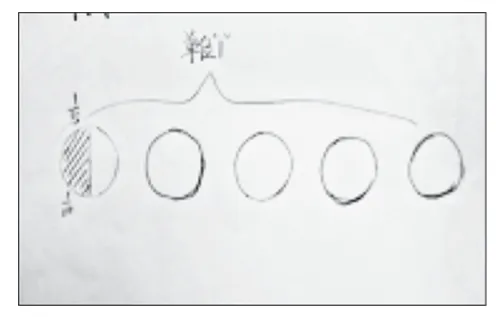
图3：用5个圆为整体1表示

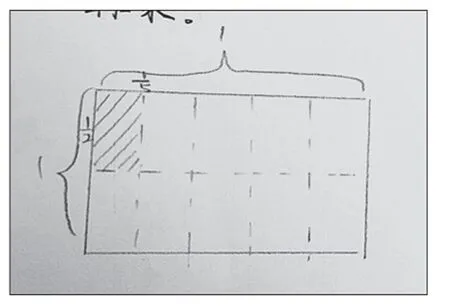
图4：用面积图表示

上图所示的这四种表示方法，孩子们是这么表述的

生甲：我们小组中有同学把一条线段看做单位1，平均分成5段，每一段就是，再×，就是再一半，这时候，这个小段，相当于原来的线段的我们认为是对的。

生乙：图2中的实线是把长方形平均分成了5个长条，虚线是把每个长条又平均分成了2份，这样一共分成了10个小长条，1个长条就是我们认为也是对的。

生丁：我们的做法其实跟图2的道理是一致的，都是把长方形先竖着分成5份，找到，再横着分成2份，找到涂上颜色，这涂上颜色的部分就是

以上4种作图，通过表述和交流，学生们突然发现，都是先画个图表示单位1，再分一分，找到再分一分，找到，最后都是把单位“1”平均分成10份，产生了新的分数单位，而新分数单位的个数都是1。这几种方法本质是一样的，只是单位“1”样式不同而已。

这些图形表征，这些语言表述，让学生在头脑中对分数单位乘法进行了丰富的表象，让算法有了算理的支撑，在求同存异的交流中，更懂得怎么去探求新知识的方法。

建构主义理论家皮亚杰说过：儿童的思维是从动作开始。因而，要促使学生思维发展，不能切断动作与思维联系。 “画一画、涂一涂、量一量、实物演示”等动手实践方式，能让学生获得最直接的体验，建构丰富的感性认识，从而理解算理，形成算法。

2.多元互化，融会贯通，让算法有更多支撑

当到达小学六年级学习分数的计算时，学生已经积累了整数乘法、小数乘法、分数意义等知识和学习经验，分数乘法的算理可以在分数与除法的关系中推理所得，也可以根据分数小数互化推理，得到解释和证明，从而使分数乘法的算理建构融会贯通。如下图所示：

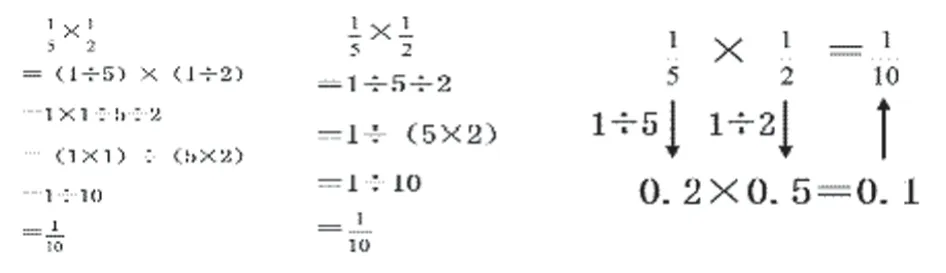
以上两类推理方法均运用了“转化”的思想方法，当学生发现，要证明分数乘法的推理是有根据的，还能通过原来学过的小数乘法、分数与除法的关系进行“转化”，其实是打开了一片的新的思维天地，方法①和②，都可以看做分数的意义的算式表述过程，而方法③把分数转化成小数再计算，当然可以证明自己的思考的正确性。

通过多元互化，融会贯通，在辨析与沟通中，学生在“同”与“不同”中越来越明晰、理解算理。

3.抽象概括，归纳梳理，从算理中提炼出算法

史宁中教授说：“数学教学的最终目标，是要让学习者会用数学的眼光观察现实世界，会用数学的思维思考现实世界，会用数学的语言表达现实世界”。知道为什么要这么算的算理后，我们要把让学生经历从算理到算法的归纳过程，通过学生观察、概括和推理，抽象出算法，就是一个建构模型的过程，因而从算理到算法，是发展学生数学思维极佳的机会，从理解算理到形成算法，是计算教学的必经之路。

师：是啊，通过多种解释，我们依然可以发现，单位分数相乘产生了新的分数单位，分数单位的数量仍然是1。为了便于记忆，我们在计算单位分数相乘时，习惯上将算法口诀化：单位分数相乘，分母相乘的积作为积的分母，分子是1。

史宁中教授说，数学技巧并不是非常重要，最关键要教孩子“怎么想”和“怎么去想”，“会不会”不是老师教出来，应该是“学生悟出来的”，重视算法提炼的过程，其实是对知识的“悟”的过程，它必须建构与对算理的理解，分数乘法算理的理解虽然有点难，但是因为有让学生动手实践、自己推理思考、感悟提炼的过程，“计算法则”不再是“习得知识”，而是“悟道”与“智慧”，因而不但使算法逐渐清晰，更使思考有随时的图像再现可能。

4.自主探究，从特殊到一般,算理随时隐现

当学生多元学习单位分数相乘的算理和算法后，引导学生自主探究“单位分数乘一般的分数”，从简单到复杂，从扶到放，学、思、用结合，引导学生理解 “为什么”,从而自主得到算法，也算是掌握思考的方法和学习的策略。

【教学片段】

学生交流中发现有如下类别：

（1）迁移——画图表示分数乘法意义中得到算法

如右图：把大长方形当作单位“1”，先竖着把单位“1”平均分成5份，取1份得到，再把横着平均分成3份，取2份，这相当于把原来的大长方形平均分成了15份，每份是，取2份，即。

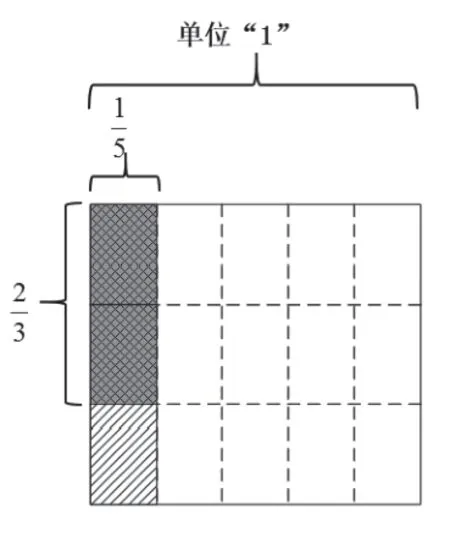
（2）拆数转化——一般分数拆成基本分数单位

而化成小数乘法来解释，或者分数与除法的关系来解释的，基本没有，说明孩子们已经从方式多样化自然而然地进行了方法的优化，而且这两种方法的思考与解释，都各有亮点，方法（1）完全理解了分数乘法的“运算的意义”，所以算理顺手就来，方法（2），学生知识现学现用，拆开分数，使他转化为我们刚刚已经学过的知识，其实学习品质已经是极高了。

5.拓展延伸，从算理到算法，形成完整建构

新课教学时，特别重视算理，当每一道题能演算出结果，算法都能隐现，就达到了算理与算法的紧密结合，使思维可以外显。当学生学完单位分数相乘、单位分数乘一般分数后，我们出示最普通的分数，让学生自主建构问题解决的模型。

学生很显然把分数乘法的算理进行了优化，喜欢把画长方形当作单位“1”，然后竖着平均分，涂色得到第一个分数，再横着平均分，涂色得到第二个分数，交叉涂色的部分就是所得的分数的结果。并且得到结论，总共是分成了5×3=15份，所以分母是15，而双重涂色的是2×4=8份，所以

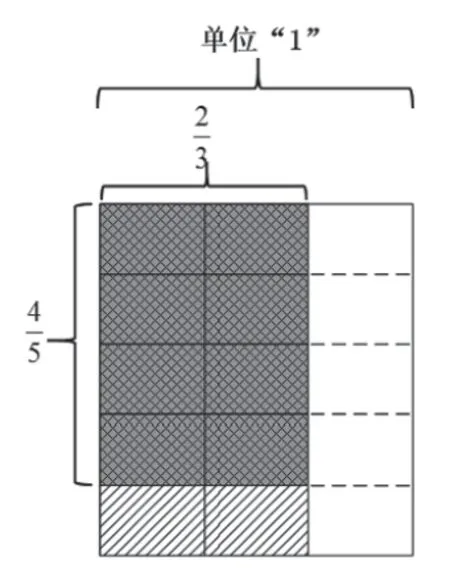
学数学不做题不行，但是大量重复操练肯定不行，数学家很多时间都在做题，但更多的时候是找模型，建构模型后的做题才是做题，所以我们小学数学的教学，也要让孩子多些思考和悟的过程，而不是把知识嚼碎了，喂进孩子嘴里，再重复操练，这将扼杀学生发现问题、思考问题，探索模型、解决问题的乐趣，更将孩子直观思维和创新能力进行扼制。计算教学，以算理探索与理解，由此摸索提炼算法，这样的过程，才是有意义的数学学习过程。这毫无意义，运算能力的培养与发展，必须结合算理来进行，无论怎样的数学教学，

综上所述，计算教学，必须让学生理解算理的基础上来掌握算法，如果用画图、直观理解等表达和解释算理——“为什么这么算”，再从算理的充分理解下，观察归纳推理计算方法，用多元建构、融会贯通，不但能让算法有了丰富的算理表象支撑，更能让数学知识的习得有一个“悟”的过程、“思考”的过程，由知道“是什么”到思考“为什么”，由“吞咽知识”到“了悟智慧”，能使学生的数学活动经验逐渐丰富，认知广度和深度扩张，思考渐成习惯，这才是我们数学计算教学要达到的目标，也是数学课应该达到的目标。