盾构隧道双层衬砌结构弯矩分配的解析模型

2019-04-02王志云李守巨上官子昌

安徽理工大学学报（自然科学版） 2019年1期

王志云, 李守巨, 上官子昌, 李浩,刘超,颜雄

( 1.大连海洋大学海洋与土木工程学院,辽宁大连 116023, 2.大连理工大学工业装备结构分析国家重点实验室,辽宁大连 116024)

在某些穿越江海水下铁路盾构隧道设计中采用双层衬砌结构形式，即在隧道盾构掘进过程中首先施工预制管片(称为初次衬砌)，在适当的时候进行现浇混凝土二次衬砌施工，二次衬砌的主要功能包括：加固初次衬砌管片、防止渗水、修正初次混凝土管片所形成隧道的线形、保证隧道内表面的光滑和防止在高水压作用下隧道上浮等。针对高水压越江海长大盾构隧道，是否有必要进行管片二次衬砌的争论、二次衬砌的结构性功能、二次衬砌力学承载特性，目前仍然是世界性的争议问题。

文献[1]采用压杆、结合面点位移耦合等技术，解决现有模型中地层与衬砌之间、双层衬砌结合面之间存在拉力以及结合面剪切应力与剪切位移无关等问题，提出适用于该模型的双层衬砌结合面和地层衬砌接触面参数计算依据，探讨结合面单元数量对分析结果的影响，研究杭长客运专线钱塘江隧道双层衬砌的力学行为。文献[2]综述我国城市地铁盾构隧道修建技术的发展历程及近期新的发展趋势，讨论了采用盾构法修建地铁隧道存在的技术问题，介绍了近期国内外盾构设备制造技术与选型技术、盾构施工对环境的影响及控制、复杂条件下盾构隧道结构性能、盾构隧道衬砌结构劣化特征与耐久性的相关技术研究与新进展。文献[3]在国内外现有单层管片衬砌和全环双层衬砌的基础上，研究提出了一种新型的“管片衬砌+非封闭内衬”的双层衬砌结构，并以武汉长江隧道盾构为例，讨论了不同支护方案条件下管片的内力分布特性。文献[4]指出隧道二次衬砌设计的争议性问题是世界性的，其主要根源在于对二次衬砌的功能看法的差异，文献[5]采用有限元方法模拟了混凝土管片及其接头承载力特性，国际隧道协会2000年颁布了隧道管片设计指南[6]，目前许多国家隧道管片设计在此基础上提出了各自的设计方法。Molinsc采用实验方法研究了管片内弯矩、轴力和剪力分布特性[7]。文献[8]研究了预应力混凝土管片衬砌中预应力的设定方法，根据对裂缝出现的不同控制要求，考虑环境条件与隧道用途要求，提出了3种预应力设定方法。还有一些研究人员通过实验的方法对在工作荷载作用下，隧道衬砌的强度和变形特性[9]，以及特殊载荷情况下隧道衬砌的破坏模式[10]进行了研究，同时对非破坏性评价技术进行了开发[11]。文献[12]研究浅埋花岗岩地铁隧道二次衬砌力学特性，采用现场监测方法得到浅埋花岗岩隧道初期支护与二次衬砌间的接触压力和二次衬砌内钢筋应力，并讨论该接触压力及钢筋应力随时间的发展规律和沿洞周的空间分布特性。文献[13]采用荷载结构模型分别计算实测和规范荷载作用下的二次衬砌结构的安全系数并进行对比分析，得出实测荷载作用下二次衬砌的安全系数远高于规范荷载作用下的安全系数。文献[14]按照二次衬砌承受全部荷载的70%，初期支护与围岩共同承担荷载30%的原则，基于荷载-结构法建立有限元模型，用其计算了某隧道工程二次衬砌设计的结构安全性。文献[15]采用有限元分析软件ADINA，对丹东某隧道进行了开挖支护过程的数值模拟，研究了多种工况条件下，二次衬砌变形发展演化规律。

目前，二次衬砌的作用机理包括以下三种模型：1)二次衬砌与初次衬砌共同作用模型；2)初次衬砌作为临时支护，二次衬砌作为单独的永久支护模型；3)初次衬砌作为单独的永久支护结构，二次衬砌只是进行防水、防腐、美观、隔热保温等辅助功能，仅仅是对初次衬砌管片加固(安全储备)模型。本文考虑二次衬砌的结构性功能，研究盾构隧道双层衬砌结构弯矩分配特性，推导其解析表达式，并通过数值算例进行验证，为盾构隧道双层衬砌结构设计提供参考依据。

1 盾构隧道双层衬砌弯矩分配特性

为了得到简化的盾构隧道双层衬砌结构模型，考虑到该结构主要承担弯矩和轴力作用，二次衬砌混凝土与初次衬砌混凝土管片之间处于受压状态，忽略二次衬砌混凝土与初次衬砌混凝土管片之间粘结力，因此将其简化为双层叠合梁结构。

简化的盾构隧道管片双层衬砌几何模型如图1所示，其中，外层为预制初次衬砌混凝土管片，其截面高度为h1，单个管片宽度为b，截面形心半径Ro，弹性模量为E1，对于C50混凝土，E1=35GPa。内层为现浇的二次衬砌混凝土，其截面高度为h2，对应的宽度为b，截面形心半径Ri，弹性模量为E2，对于C30混凝土，E2=30GPa。盾构隧道混凝土管片双层衬砌简化为双层叠合梁，在外侧的土水压力作用下，将发生弯曲变形。

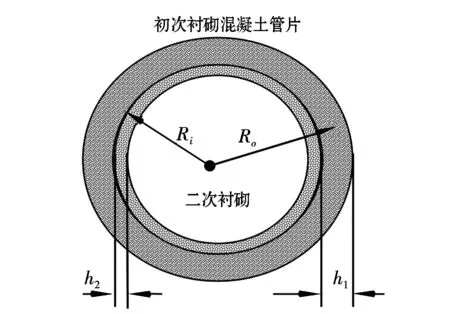
图1 简化的盾构隧道混凝土管片双层衬砌

根据材料力学中梁的弯矩与曲率的关系，初次衬砌管片所承担的弯矩为

M1=E1I1Δφ1

(1)

式中：M1为初次衬砌混凝土管片的弯矩，I1为初次衬砌混凝土管片的惯性矩，I1=bh13/12，Δφ1为弯矩作用下混凝土管片曲率增量。

Δφ1=φ1-φo

(2)

式中：φ1为弯曲后混凝土管片形心的曲率，φo为弯曲前混凝土管片形心的曲率。根据曲率与曲率半径的关系，得

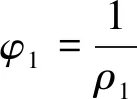
(3)

式中：ρ1为弯曲后混凝土管片形心的曲率半径。

(4)

假设在弯矩作用下，初次衬砌混凝土管片形心的曲率产生一个微小的增量，即曲率半径产生一个微小的减少量

ρ1=Ro-ΔR

(5)

式中：ΔR为初次衬砌混凝土管片弯曲时形心的曲率半径减少值。将(5)式带入(3)式，得

(6)

考虑到在土压力荷载作用下隧道双层衬砌处于小变形状态，即Ro≫ΔRo。将(6)式和(4)式带入(2)式，得

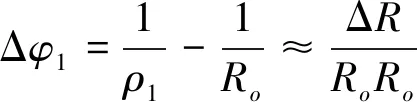
(7)

于是，初次衬砌管片所承担的弯矩为

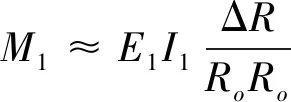
(8)

同理，在弯矩作用下，二次衬砌混凝土的所承担的弯矩为

M2=E2I2Δφ2

(9)

式中：M2为二次衬砌混凝土的弯矩，I2为二次衬砌混凝土的惯性矩，I2=bh23/12，Δφ2为二次衬砌混凝土曲率增量。

Δφ2=φ2-φi

(10)

式中：φ2为弯曲后二次衬砌混凝土形心的曲率，φi为曲率前二次衬砌混凝土形心的曲率。

(11)

式中：ρ2为弯曲后二次衬砌混凝土形心的曲率半径。

(12)

考虑到隧道双层衬砌处于小变形状态[16]，弯曲后二次衬砌混凝土形心的曲率半径的减少量与初次衬砌混凝土管片曲率半径的减少量近似相等

ρ2=Ri-ΔR

(13)

于是，得到

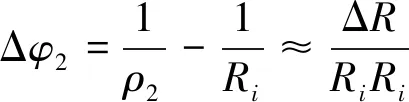
(14)

二次衬砌混凝土承担的弯矩为

(15)

因此，初次衬砌混凝土管片所承担弯矩与总弯矩的比为

(16)

令初次衬砌混凝土管片截面形心半径与二次初次混凝土截面形心半径比为ψ

(17)

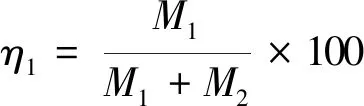
(18)

二次衬砌混凝土所承担弯矩与总弯矩的比为

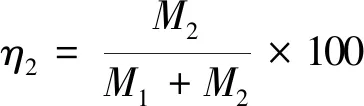
(19)

计算结果如图2～图3所示。

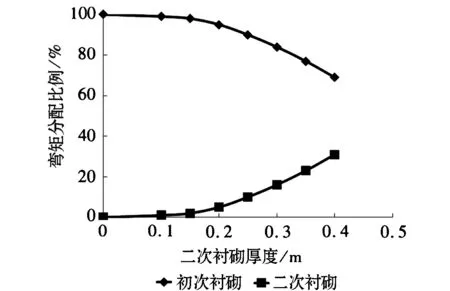
图2 弯矩分配比例随二次衬砌厚度的变化(h1=0.5m)

图3 弯矩分配比例随二次衬砌厚度的变化(h1=0.6m)

从图2中可以看出，在常见设计的双层衬砌厚度条件下(管片厚度h1=0.5m，二次衬砌混凝土厚度h2=0.2m)，初次衬砌管片所分担总的弯矩94%，而二次衬砌混凝土所分担总的弯矩仅仅占6%。因此，二次衬砌混凝土的结构性功能可以忽略不计。图3给出了h1=0.6m时弯矩分配比例随二次衬砌厚度的变化特性。解析解所得到弯矩分配比例的与文献[17]实验结果基本一致，验证了本文所提出方法的有效性。

2 解析模型正确性的有限元数值验证

算例1为武汉长江地下铁路隧道，考虑水深30m、隧道顶板以上土层厚度20m，管片外径11.4m，内径10.4m，管片厚度h1=0.5m，宽度取单位宽度b=1m，二次衬砌混凝土厚度h2=0.2m。混凝土管片的弹性模量为34.5GPa，二次衬砌混凝土的弹性模量为30.0GPa。土层的平均密度为1 900kg/m3，平均弹性模量20MPa，采用水土合算土压力模型，泊松比[18]取为μ=0.42。采用有限元方法计算得到初次衬砌管片的最大弯矩为M1max=1 410kN·m，二次衬砌混凝土的最大弯矩为M2max=57kN·m。

算例2[19]隧道埋深21.6m，水深3.4m，管片外径10.8m，内径9.8m，初次衬砌管片厚度h1=0.5m，宽度取单位宽度b=1m，二次衬砌混凝土厚度h2=0.2m。混凝土管片的弹性模量为34.5GPa，二次衬砌混凝土的弹性模量为30.0GPa。土层的平均密度为1 900kg/m3，平均弹性模量20MPa，泊松比为μ=0.42。采用有限元方法计算得到初次衬砌管片的最大弯矩为M1max=838kN·m，二次衬砌混凝土的最大弯矩为M2max=37kN·m。

算例3为承受均布土水压力荷载的双层混凝土叠合梁直梁，跨度L为7.85m，h1=0.5m，h2=0.2m，宽度取单位宽度b=1m，两端简支，上层梁(初次衬砌管片)弹性模量E1=35GPa，下层梁(二次衬砌混凝土)弹性模量E2=30GPa。顶部承受均布土水压力荷载p=40kPa。采用有限元方法计算得到上层梁的最大弯矩为M1max=261.66kN·m，下层梁的最大弯矩为M2max=9.380kN·m。

有限元数值模拟的三个例子弯矩分配比例与解析解得到的解如表1所示，从表1中可以看出，初次衬砌管片所分担总的弯矩94%以上，而二次衬砌混凝土所分担总的弯矩仅仅占6%以下。因此，二次衬砌对结构的承载能力贡献较小，其更主要的作用在于防水、抗震、抗浮和补强加固作用。