偏度最大化多通道逆滤波语声去混响研究∗

郭 颖 彭任华 郑成诗† 李晓东

(1中国科学院噪声与振动重点实验室(声学研究所) 北京 100190)

(2中国科学院大学 北京 100049)

0 引言

在一个封闭空间中，传声器拾取的语声信号既包括直达声，也包括通过墙壁和天花板等反射的混响声。房间混响会引起谱染色，影响语声质量，降低语声可懂度，进而严重降低语声识别、语声分离等应用的性能。随着说话人与传声器距离的增加以及房间混响时间的增加，混响所带来的影响也会越严重。

去混响方法通常可以分为以下几类：(1)波束形成[1]，该方法是一种空间滤波技术，广泛应用于雷达、声呐、远程通讯、声学、图像处理等多种领域[2]。在声学信号处理中，用于噪声环境下的声源提取以及混响抑制。该方法往往需要信号的波达方向(Directions of arrival,DOAs)作为先验信息，而且为了达到比较理想的去混响效果，需要相对较多的传声器个数以及较大的传声器阵列孔径，从而使直达方向的增益足够大。(2)谱增强[3−4]，Lebart等[5]提出利用谱减法实现无噪声情况下的语声去混响。通常用于晚期混响抑制，该类方法需要根据房间的混响时间来估计混响的能量。Fang等[6]用基于相干函数的方法实现去混响。(3)线性预测(Linear prediction,LP)残差增强，Peng等[7]的工作说明了晚期混响在LP残差域相对较白。文献[8]采用约束最小均方误差LP残差估计方法去除晚期混响和噪声，相比于传统的LP残差域处理方法和谱减法性能有很大的提升。文献[9]利用多级线性预测实现晚期混响抑制。(4)逆滤波，该类方法直接估计引起房间混响的房间脉冲响应(Room impulse response,RIR)，通过对观测信号进行解卷积得到原始信号。在实际应用场景中，房间脉冲响应通常是未知的，而且会随着声源移动或房间状态(如温度和湿度等)的改变而变化。因此，本文研究盲反卷积的方法。基于随机变量非高斯性极大的准则，混响信号可以假设为独立同分布(i.i.d)的语声信号进行延迟、加权的结果，依据中心极限定理[10]，混响信号可以近似为高斯分布。高阶统计量是衡量非高斯性的重要参量，语声信号是典型的非高斯信号，因此采用高阶统计量可实现语声分离和去混响。

文献[11]提出一种最大化线性预测残差四阶统计量峰度(Kurtosis)的去混响方法，证明了该方法比传统的波束形成方法具有更有效的去混响效果。文献[12]在此基础上提出单通道频域实现，通过实验说明该方法在0.2∼0.4 s的混响时间范围内有效，而在混响较强的环境下该方法失效。应用峰度准则的方法去混响性能有限，文献[13]采用三阶统计量偏度(Skewness)对具有不对称概率密度分布的信号进行盲反卷积，文献[14]提出最大化线性预测残差偏度的单通道逆滤波方法，通过实验说明了足够长的纯净语声信号概率密度分布呈现出明显的不对称特性，该方法相比于峰度准则在较强混响下性能更优，而且鲁棒性更强。直接对混响语声信号进行线性预测得到的线性预测系数存在一定的偏差，影响房间脉冲响应逆滤波的准确度，文献[15]从语声信号的产生模型出发，将混响语声信号的盲逆滤波分解为预测误差滤波器(Prediction error fi lter,PEF)的估计和房间脉冲响应逆滤波器的估计两部分。

本文提出一种基于高阶统计量的多通道语声去混响方法，该方法首次用多通道语声信号线性预测残差的偏度构造代价函数，以语声去混响重建信号线性预测残差的偏度最大化为目标，自适应地更新通道逆滤波器。同时为了得到更准确的通道逆滤波器估计，提出联合估计通道逆滤波器和语声产生系统逆滤波器的新方法。该方法相比于已有的线性预测残差域峰度最大化的多通道去混响方法，计算量更低，而且具有更好的去混响效果，特别是在混响时间较长的环境下性能更为突出，同时对噪声的鲁棒性更强。

1 偏度最大化多通道房间脉冲响应逆滤波

1.1 算法理论模型

混响语声模型可以表示为

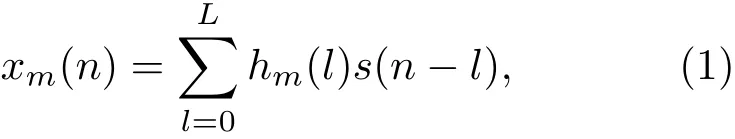
其中，传声器个数为M(M>2)，xm(n)为第m个传声器拾取的混响语声信号，s(n)为目标语声信号，{hm(l)}表示声源到第m个传声器的L+1阶时不变的房间脉冲响应。

语声信号从产生、经过房间反射到被传声器拾取所经过的声学系统可认为是语声产生系统和房间声学系统的串联系统。其中语声信号的产生过程可建模成一个时变的自回归(Autoregressive,AR)过程[16]，考虑语声信号的短时平稳特性，第i帧的声源信号可以表示为

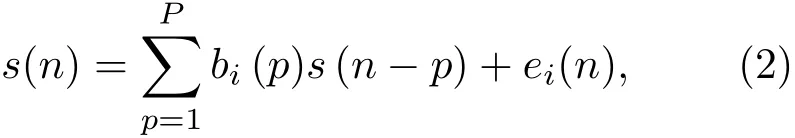
其中，{bi(p)}为P阶预测系数，语声产生系统的传递函数B(z)是{bi(p)}的Z变换，可以用一个阶数为P的时变FIR滤波器来表示，其逆滤波器称为预测误差滤波器。房间声学系统的传递函数H(z)可以用一个阶数为L的时不变FIR滤波来表示。因此，观测信号x(n)是在e(n)激励下，经过语声产生系统B(z)和房间声学系统H(z)共同作用的输出结果。

盲去混响的目标是在无任何房间先验知识的前提下，仅通过传声器观测信号x(n)去除由房间声学系统H(z)所引起的混响，恢复声源信号s(n)。因此，一个重要的问题就是在盲逆滤波过程中，如何将房间脉冲响应的逆滤波从整个系统的逆滤波中分离出来，即去掉声道滤波对房间脉冲响应逆滤波所造成的偏差。一种常用的方法是首先对混响语声信号直接进行线性预测预白化处理，阶数一般取为10，然后在线性预测残差域进行逆滤波。考虑线性预测系数受语声信号中混响的影响，直接对混响信号进行线性预测求得的预测系数存在偏差，更为准确的方法可以采用预测误差滤波器与房间脉冲响应逆滤波器联合估计。图1展示了联合估计算法的实现框图，考虑时域实现收敛较慢，甚至可能不收敛，因此本文采用频域方法实现。首先用时不变的房间脉冲响应逆滤波器在频域对观测信号进行滤波后，再通过时变的预测误差滤波器，得到线性预测残差信号，以残差信号的偏度最大化为目标，计算滤波器的更新梯度，进而更新房间脉冲响应逆滤波器，利用更新的逆滤波器对混响信号进行滤波，重构出逆滤波后的语声信号。算法记为基于偏度的预测误差滤波器与房间脉冲响应逆滤波器的联合估计方法，即MSJE-IF-MSD(Maximum-skewness joint estimation based-inverse f i ltering for multichannel speech dereverberation)，简化为MSJE。

gm表示通道m的L阶自适应房间脉冲响应逆滤波器系数，gm=[gm(0),···,gm(L−1)]T；为第m通道的房间脉冲响应逆滤波器系统传递函数。这里需要假设每个通道的房间传递函数G1(z),···,GM(z)之间没有共同的零点。进而可以得到逆滤波后重构的语声信号：

其中，xm(n)=[xm(n),···,xm(n−L+1)]T。根据语声信号的短时平稳性，将逆滤波输出y(n)分帧后通过时变的预测误差滤波器{ai(p)}，得到第i帧线性预测残差信号di(n)：

用向量形式表示：

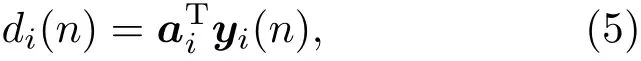
其中， ai= [1,−ai(1),−ai(2),···,−ai(P)]T，yi(n)=[yi(n),yi(n−1),···,yi(n−P)]T，P 为预测误差滤波器阶数。为预测误差滤波器系统传递函数。

理想情况下最终得到的di(n)与激励信号ei(n)等价，只存在微小的延迟和幅度变化。因此，问题可退化为房间脉冲响应逆滤波器g和预测误差滤波器a的估计，g=[,···]T，a=[,···]T，S为线性预测总帧数。

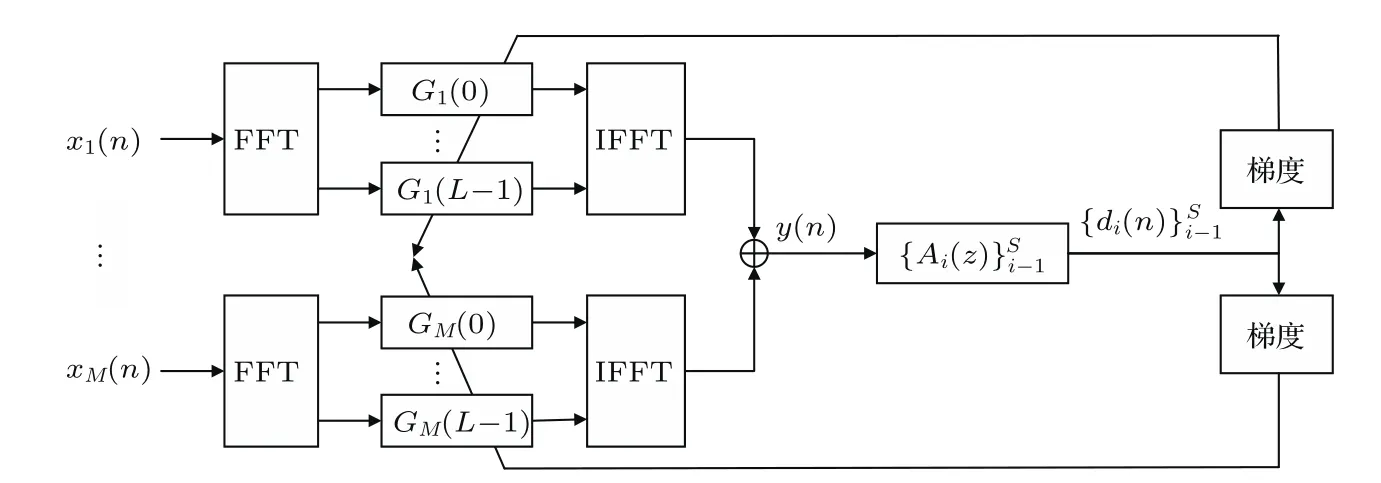
图1 MSJE算法框图Fig.1 Schematic diagram of MSJE

1.2 目标函数

根据上面的讨论，需要建立合适的目标函数来估计g和a。考虑逆滤波后残差信号{d(n)}样本间的相关性最小，采用交互信息作为目标函数[15]：

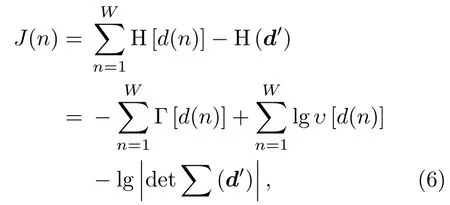
其中，W为样本点数，H(ξ)表示随机变量ξ的微分熵，d′=[d(W),···,d(1)]T，υ[d(n)]表示d(n)的方差，∑(d′)=E[d′d’T]。Γ[d(n)]表示d(n)的负熵，用来衡量信号的非高斯性，可以用高阶统计量表示，三阶统计量——偏度用来衡量概率密度分布的偏斜程度，定义为

其中，µ3为三阶中心距，σ为标准差。相对于四阶统计量峰度，偏度的优势主要体现在衡量一些概率密度分布具有不对称性的声源信号非高斯性上。

本文考虑偏度作为衡量语声信号非高斯性的准则，根据公式(7)，目标函数可进一步表示为

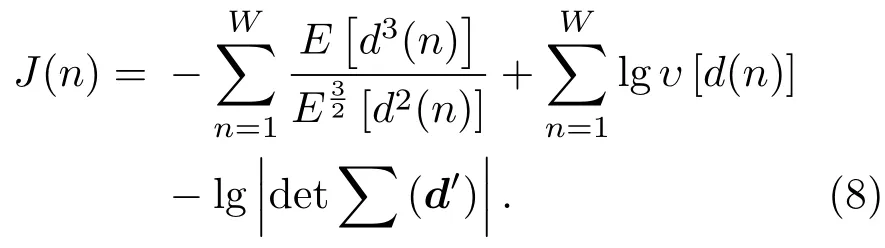
因此可以建模为下面的优化问题：

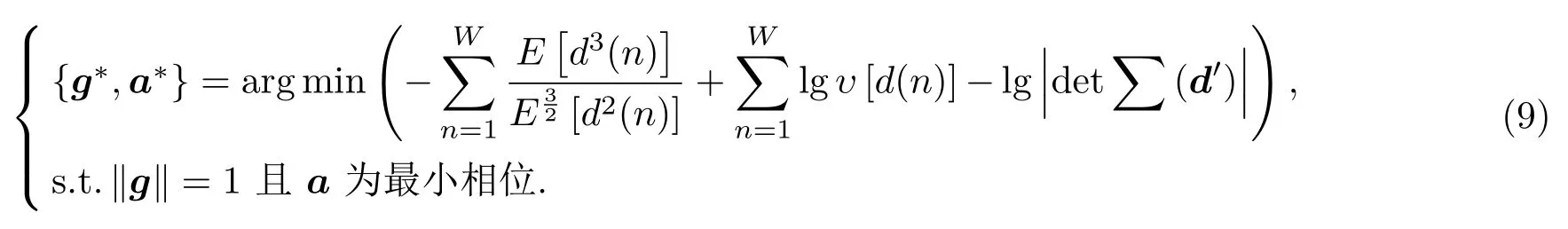
约束条件∥g∥=1保证了房间脉冲响应逆滤波器的归一化。同时为了使系统稳定，应保证预测误差滤波器a的最小相位特性。

1.3 预测误差滤波器的估计

由于高阶统计量会使预测误差滤波器非最小相位，因此该部分的估计只考虑二阶项作为目标函数，表示为

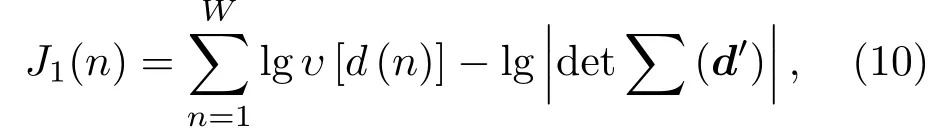
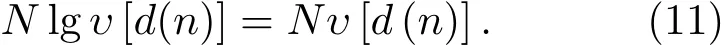
具体实现：首先对逆滤波后的输出信号y(n)进行分帧得到yi(n)，逐帧通过线性预测估计yi(n)的预测误差滤波器系数ai。而线性预测可以保证估计得到的预测误差滤波器的最小相位性。

1.4 房间脉冲响应逆滤波器的估计

通常语声信号的激励信号为超高斯分布，它的二阶矩相对于高阶矩可以忽略。因此，该部分只考虑公式(8)中的三阶项部分。目标函数可化简为

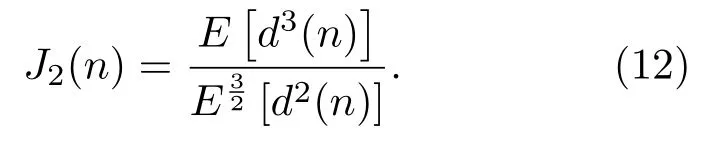
采用梯度下降法对每个通道的滤波器gm进行单独更新，更新方程为

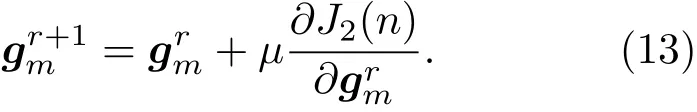
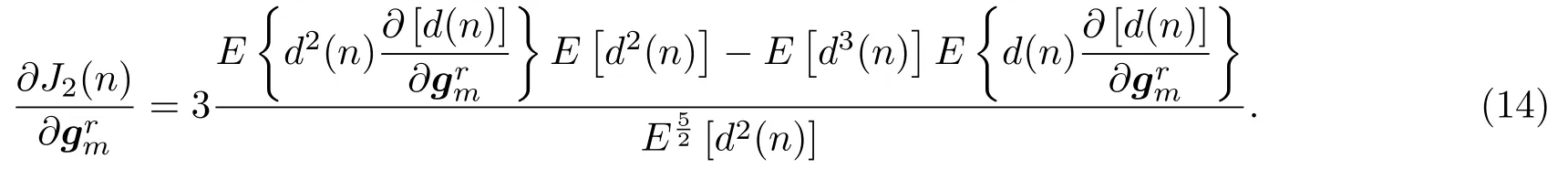
其中，Xm(n)=[(n),···,(n−P)]T。对第i帧残差信号的梯度进一步推导：

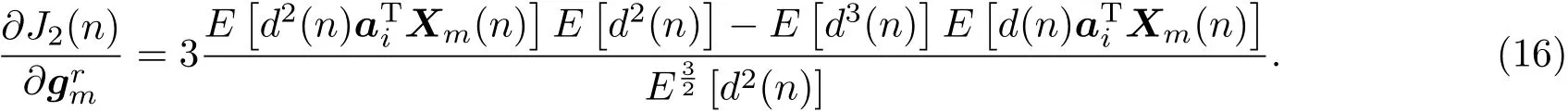
为了进一步简化，忽略式(16)的时间依赖性，令rm(n)=Xm(n)，梯度近似为

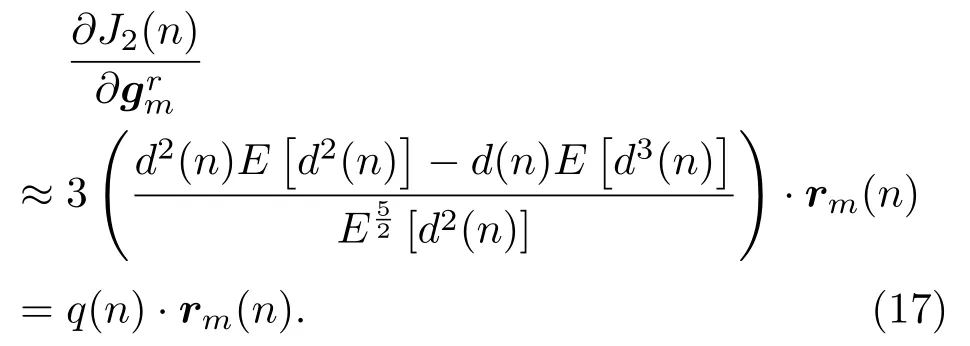
逆滤波器在频域进行更新。将更新后的线性预测残差信号rm(n)分成长度为L的块，并将每一块补0至长度为2L，对每一块计算长度为2L的傅里叶变换(Fast Fourier transform,FFT)。将q(n)分成长度为2L的块，重叠50%，对每一块计算长度为2L的FFT。设分块个数为T，得到频域自适应更新方程：

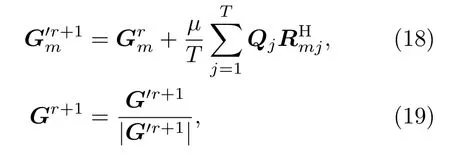
1.5 联合估计策略

上述目标函数的简化以及迭代估计两个逆滤波器需要基于如下假设：当g固定时，最小化二阶项的同时也会使整体目标函数最小化；同理，当a固定时，最大化三阶项也会使整体目标函数最小化。根据以上分析，迭代更新预测误差滤波器和房间脉冲响应逆滤波器。对观测信号，首先通过房间脉冲响应逆滤波器进行逆滤波后，再通过预测误差滤波器，得到更新后的残差信号；以残差信号的偏度最大化为目标，通过梯度下降法更新房间脉冲响应逆滤波器，迭代更新直至滤波器收敛，重构出逆滤波后的语声信号。

作为联合估计的替代，另外一种比较简单的实现可以直接对观测信号进行线性预测预白化处理，在线性预测残差域上求解房间脉冲响应逆滤波器。该方法可以认为近似于MSJE预测误差滤波器只迭代一次的情况。为了对比，将最大化线性预测残差偏度的多通道逆滤波语声去混响方法记为MLPRS-IF-MSD(Maximum linear prediction residual skewness-based inverse f i ltering for multichannel speech dereverberation)，简化为MLPRS。

2 仿真和实验研究

2.1 仿真

采用镜像法[17]得到的4通道的RIR，声源信号由TIMIT数据库中选取的100段男声和100段女声语声段构成，将其与不同混响时间的RIR卷积得到混响语声信号。在模型中，4个传声器分布在尺寸为5.5 m×4.5 m×3.5 m的矩形房间内。声源(红色圆点)与传声器阵列(灰色圆点)在房间内的分布示意图如图2所示，传声器间隔0.2 cm按线型摆放，与声源距离d0=3.3 m。

混响时间和声学比是影响混响声场中的语言清晰度的两个独立参量，混响声场中的清晰度与混响时间(RT60)和声学比乘积的对数成反比变化[18]。混响时间增加和声源距传声器距离增大都会独立地增加混响强度[19]，RT60会导致语声频谱模糊，而d的增加会引起谱染色。在本实验中，我们考虑固定声源到传声器的距离d，改变RT60的大小，评价不同混响强度下的算法去混响性能。以下实验中帧长N取512(32 ms)，步长µ设为 e−9。

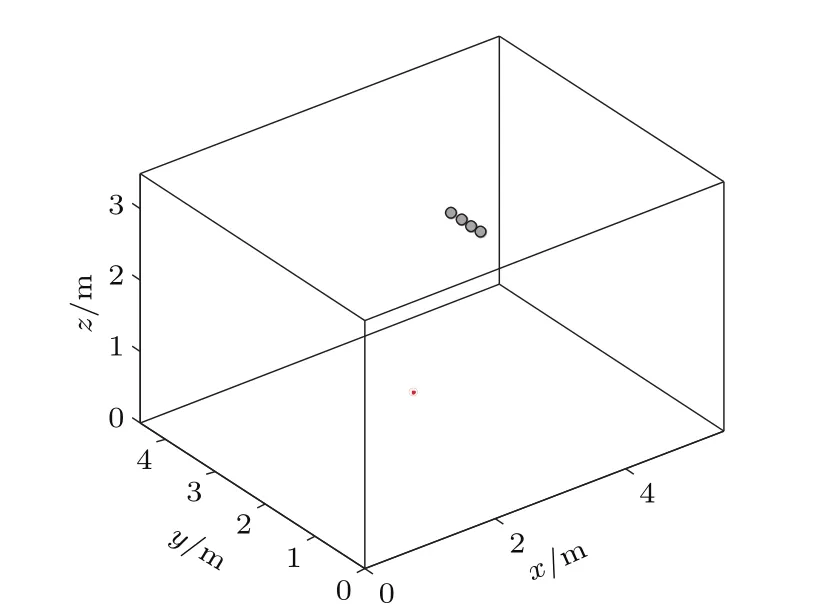
图2 传声器位置示意图Fig.2 Diagram of the microphone position

2.1.1 滤波器阶数选择

滤波器的阶数L理论上应与混响时间(RIR的样本点数)对应，即L=RT60(s)×fs(Hz)，其中采样率fs=16000 Hz。混响时间越长，滤波器长度也相应的增加。而且，滤波器阶数增加会导致计算复杂度增加；滤波器阶数增加，逆滤波后信号的延迟也会增加(RIR与逆滤波器的卷积会使逆滤波后的冲激响应与原RIR之间存在近似L的延迟)。因此滤波器阶数的选择应该在理论值的基础上，结合实际效果选择尽量小的值且能保证逆滤波的性能。本文通过实验验证，给出一定混响时间范围的最小滤波器阶数。文献[14]给出了单通道线性预测残差偏度逆滤波算法的最小滤波器阶数。表1给出本文提出的MLPRS和MSJE算法的最小滤波器阶数。

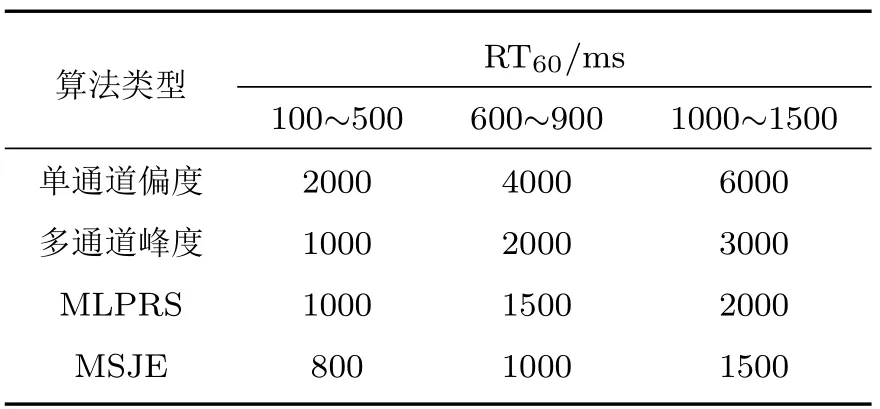
表1 不同混响时间下的滤波器阶数选择Table 1 Selection of f i lter order for dif f erent reverberation times

对比本文方法和已有的单通道偏度准则方法，利用多通道数据可以有效减少滤波器阶数，而且算法对滤波器阶数的选择不敏感；同时，采用偏度准则相比于峰度准则最小滤波器阶数也有明显的下降；采用联合估计的MSJE方法可以进一步减少滤波器阶数。滤波器阶数越少，算法的计算复杂度也会降低。

2.1.2 混响抑制性能分析

为了评估本文算法的混响抑制性能，这里采用直达-反射路径能量比(Direct-to-reverberation ratio,DRR)和主观语声质量评估[20](Perceptual evaluation of speech quality,PESQ)作为衡量指标，用于比较本文方法和Gillespie等[11]提出的峰度最大化多通道逆滤波语声去混响方法(以下简称峰度算法)。DRR可以用公式(20)进行计算：

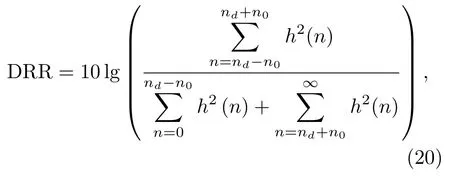
其中，直达信号在第nd个采样点到达，直达路径的能量用冲激响应峰值周围8 ms(即n0=128个采样点)的信号能量计算。因此，DRR通过直达路径能量与反射路径的总能量的比值来计算。图3为RT60=1 s时，测试语声信号在0∼4 kHz部分的语谱图及逆滤波后的房间脉冲响应。

本文研究的方法均为在房间脉冲响应未知情况下的多通道盲逆滤波算法，这里给出房间脉冲响应仅为了分析和比较逆滤波的结果。从图3中的语谱图可以看出，对于RT60=1 s混响时间比较长的情况，已有的多通道峰度准则方法表现一般。而用本文提出的多通道偏度准则方法(图3(c)，图3(d))语谱图的模糊程度明显下降，模糊的频谱结构变得清晰，采用联合估计的多通道偏度算法表现出了更好的结果。从房间脉冲响应的逆滤波结果来看，三种方法逆滤波后的RIR均有比较明显的单一峰值。

图4给出了本文提出算法在不同混响时间下的平均DRR及PESQ得分。在混响时间较短时，基于峰度的方法与本文提出的基于偏度的方法结果相近；而当混响时间较长时，本文提出的基于偏度的方法要明显优于基于峰度的方法，且随着混响时间的增加，这种优势会越明显。且本文提出的MSJE在不同混响时间下的DRR整体优于MLPRS。

比较本文提出的两个算法与峰度算法的PESQ得分，可以看出，在不同混响时间下本文提出的基于多通道偏度的去混响算法(MSJE，MLPRS)都较已有的基于多通道峰度的去混响算法性能有很大提升。基于峰度的方法对于混响时间较长的情况效果不理想。从整体上看，对于该组仿真的混响数据，除了RT60=200 ms时MLPRS方法的PESQ得分更高一些，其他情况下MSJE较MLPRS算法的PESQ得分都略有提升。

图3 RT60=1 s时逆滤波后的语谱图及房间脉冲响应Fig.3 Equalized speech spectrogram and impulse response with RT60=1 s

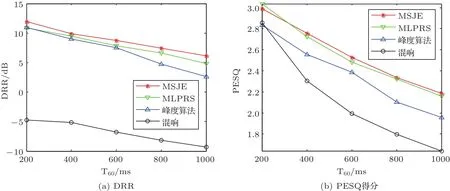
图4 提出算法在不同混响时间下的DRR以及PESQ得分Fig.4 DRR and PESQ score of the proposed algorithms for dif f erent reverberation times

2.1.3 高斯噪声环境下算法鲁棒性

该实验测试本文提出算法在加性高斯白噪声环境下的去混响性能。用PESQ得分和语声-混响调制能量比(Speech-to-reverberation modulation energy ratio,SRMR)[21]作为评价指标。

图5给出了对RT60=400 ms时的传声器阵列信号加入不同信噪比的高斯白噪声，逆滤波后的信号平均PESQ得分和平均SRMR。峰度算法对信噪比低于20 dB输入信号失效，对房间脉冲响应的逆滤波无法得到单一峰值的结果；本文提出的MLPRS算法对低于10 dB的输入信号失效，但去混响效果明显优于峰度方法；而采用联合估计的MSJE算法对测试的所有信噪比下的数据都能达到比较好的效果。本文提出的基于偏度的多通道逆滤波方法在高斯白噪声环境下的去混响性能比已有的基于峰度的多通道逆滤波方法有很大提升，提出方法对高斯噪声的鲁棒性更强。

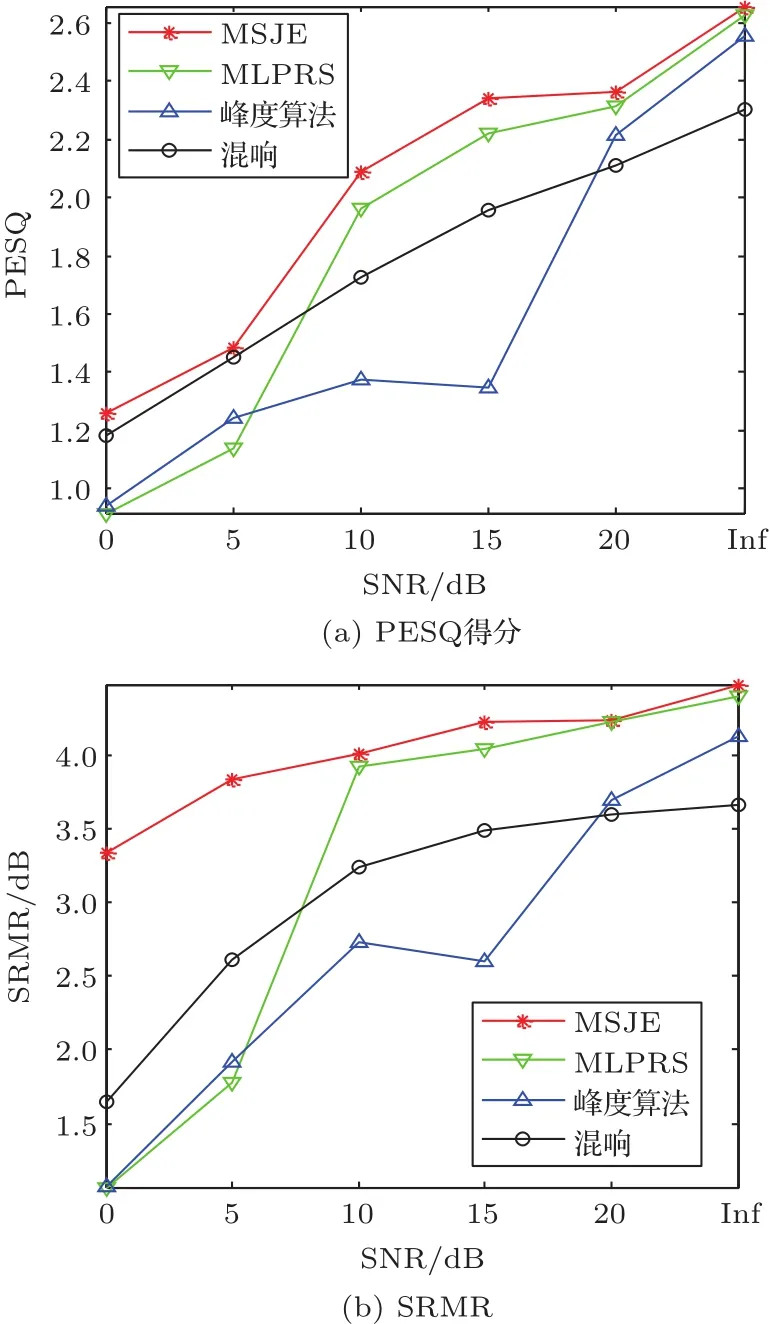
图5 提出算法在RT60=400 ms不同噪声环境下的PESQ得分以及SRMRFig.5 PESQ score and SRMR of the proposed algorithms for dif f erent noisy conditions with RT60=400 ms

在高斯白噪声环境下，影响本文算法去混响性能的因素有如下两个方面：一方面，当信号信噪比过低时，会引起线性预测模型谱密度产生畸变，使谱估计的质量受到损失，LP系数的估计变得不准确。另一方面，加性噪声的存在使信号的概率密度分布更趋于高斯分布，会改变自适应滤波过程中高阶统计量局部极大值点的位置，相比于没有噪声的情况使目标函数收敛到次极大值点，从而降低逆滤波的性能。提出的偏度方法相较于峰度方法对高斯噪声的鲁棒性更强，其原理可以通过以带有加性噪声的信号作为输入，计算两种算法的梯度来直观解释。峰度方法的梯度中受加性噪声影响的项更多，不稳定因素更多，因此峰度方法相比于偏度方法对加性噪声更加敏感。MSJE方法采用预测误差滤波器与房间脉冲响应逆滤波器的联合估计方法，使LP系数的估计更为准确，减弱了上述第一个因素的影响，因此相较于MLPRS方法对噪声的鲁棒性更强一些，在信噪比较低的情况下能更准确地估计逆滤波器。

2.1.4 计算复杂度

采用峰度和偏度准则的计算复杂度差别主要体现在梯度上，基于偏度准则的更新梯度表示为公式(17)，峰度准则的更新梯度可以进行类似的推导，最终表示为

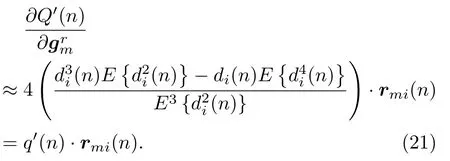
在计算梯度过程中q′(n)相比于q(n)在计算时多一次乘法，因此偏度方法相比于峰度方法计算量更低。另一方面，表1给出了两种算法在不同混响时间情况下所需的最小滤波器阶数，偏度算法所需的滤波器阶数更少，也同时降低了算法的计算复杂度。

2.2 实际环境录音仿真测试

为了更合理地评估提出算法的去混响性能，本实验采用实际环境录音的多通道房间脉冲响应数据库[22−23]与TIMIT数据库的20 s纯净语声信号进行卷积作为测试信号，测试算法对不同声学比位置处(改变d)拾声信号的去混响性能。房间大小6 m×6 m×3 m，混响时间RT60≈0.4 s，混响半径rc为1.02 m。声源位置与传声器距离d分别为1 m、2 m、4 m，对应拾声位置处的声学比分别为1.06、0.26、0.07。选取角度θ= −80◦,···,80◦，对间隔40◦测试的RIR进行处理，所用传声器个数为4，传声器间隔8 cm摆放。为了更全面地评估，实验对混响半径以内(d=1 m)的信号也进行了测试。改变声源与传声器阵列的距离d，对相同的距离每隔40◦测试一组数据，用PESQ得分作为去混响性能的评估指标。表2为实验结果。图6为改变声源与传声器阵列距离，对每组不同方向的实验结果取平均值得到的柱状图。

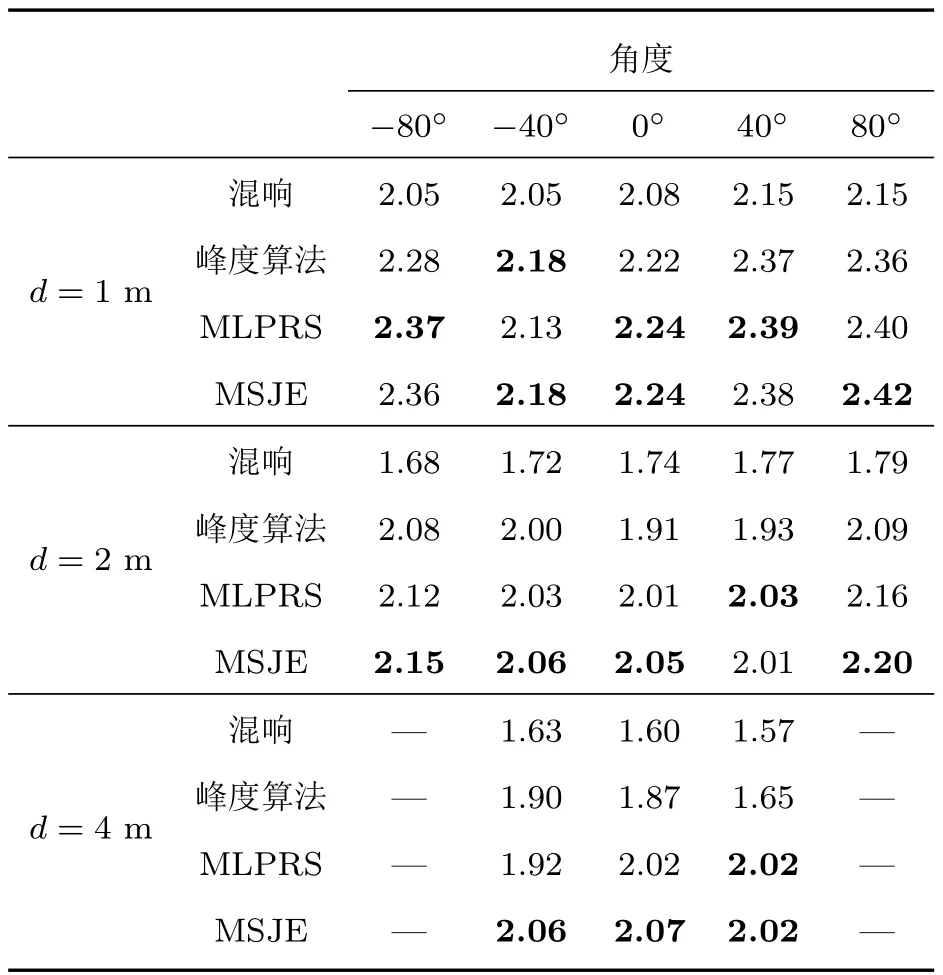
表2 实际环境录音测试结果Table 2 Recording test results in real rooms

图6 声源距传声器不同距离时算法平均PESQ得分Fig.6 Average PESQ score of the proposed algorithms for dif f erent distances between source and microphone array

该实验验证了提出算法在不同混响强度下的去混响性能均优于峰度算法，且对于在声学比远小于1位置拾声的强混响信号，本文算法的优势更为明显。

为了进一步验证算法对汉语的有效性，采用20 s“GSBM 6001-89”国家标准样件中的有代表性的两段分别由男女声朗诵的《美谈不美》纯净语声信号与上述RIR数据的卷积作为测试数据，随着声源与传声器距离的改变对标准样件添加了不同强度的混响，得到的结果如图7所示。该实验验证了算法对于处理汉语以及男女声信号的有效性。

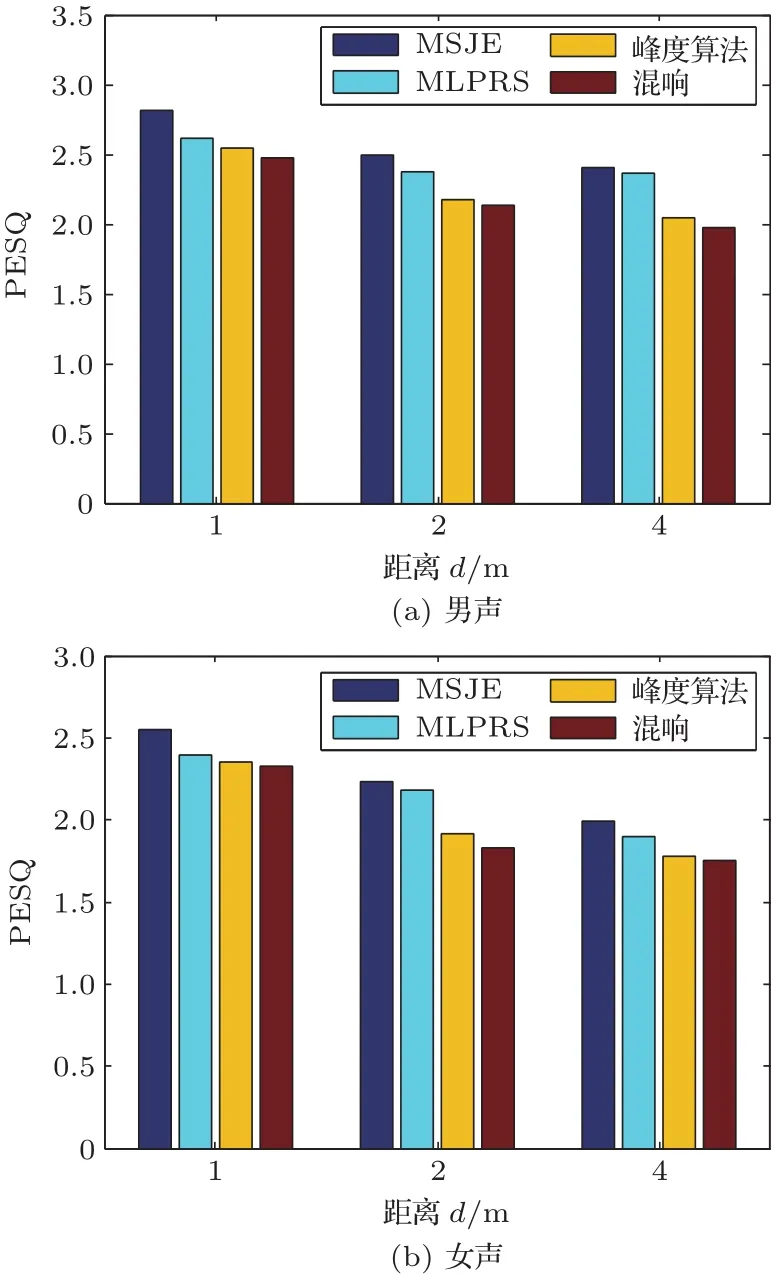
图7 声源距传声器不同距离时算法对汉语信号处理的PESQ得分Fig.7 PESQ score of the proposed algorithms for Chinese language signals at dif f erent distances between source and microphone array

3 结论

本文提出了基于偏度的多通道房间脉冲响应逆滤波方法。该方法不需要已知房间脉冲响应或波达方向的先验知识，采用非高斯性极大的准则实现盲逆滤波。实验结果表明，相比于基于四阶统计量峰度的方法，本文提出方法具有更好的去混响效果，尤其在混响较强的情况下优势更为明显，且算法复杂度更低，对高斯噪声的鲁棒性更强。应该指出的是，本文所提的方法主要用于抑制早期混响所引起的谱染色现象，而对较长混响时间所引起的拖尾现象抑制不明显，结合谱减法等后处理方法可以对残余晚期混响进行抑制，进而进一步提升可懂度。其次，在研究中发现，在混响较强情况下，相比于多通道方法，单通道算法表现出了明显的局限性。另外，在实际应用中，本文所提方法的实时处理问题也是值得进一步深入研究的。