一道绝对值型函数的最值问题探究

浙江省金华市第六中学 (321000)

张剑平

2018年浙江省名校协作体高三联考数学试题的第17题十分抢眼，属一类绝对值型函数最值问题.考试结束后，很多学生表示无从下手，利用传统的分类讨论去绝对值过程繁琐，在有限的时间难以完成.笔者对此题进行了一番探究，挖掘其背景，借助高等数学知识得到一种新的解法.深受启发，现将其整理成文，旨在与同行交流.

一、背景解读

图1

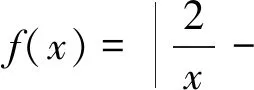
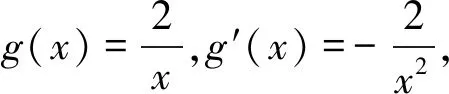
解法溯源：上述利用绝对值的几何意义求解m的最大值避免了繁琐的讨论过程，此题蕴涵着高等数学背景知识，解法的依据是切比雪夫最佳逼近直线理论：

设函数f(x)是定义在[a,b]上的连续函数，在[a,b]上有二阶导数，且f″(x)在[a,b]上不变号，则存在[a,b]上的线性最佳逼近多项式p1(x)=kx+b,它的几何直观如图2：

图2

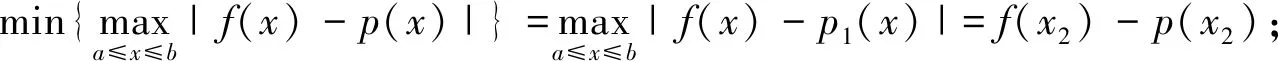
二、试题链接

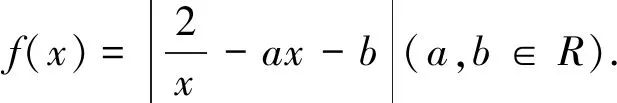
C.(-∞,1]D.(-∞,2]

图3

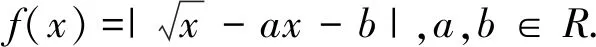
(1)当a=0，b=1时，写出函数f(x)的单调区间；

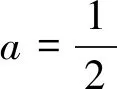
(3)若对任意实数a，b，总存在实数x0∈[0，4]使得不等式f(x0)≥m成立，求实数m的取值范围.

图4

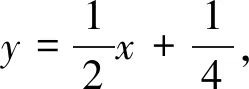
三、教学启示

浙江省近年的学业水平考试及联考试卷均出现了与切比雪夫最佳逼近理论相关的题型.由此启示一线数学教师需要在学科底蕴的厚实上下功夫，能够站在更高的高度俯视数学，并借助高等数学知识背景审视问题的本质，这有利于重新认识一些创新解题方法的源与流，从而摆脱题海战术，提高教学效率.