“圆”来如此话椭圆——例谈伸缩变换在解决椭圆问题中的应用

江苏省苏州实验中学 (215009)

张文海

苏教版高中数学教材选修系列4-2中专题“矩阵与变换”向学生介绍了图形变换和数学表示之间的紧密联系，同时揭示了变换前后几何图形的相关性．利用伸缩变换解决一些几何题目，以较高的观点来研究初等几何，可以使问题变得更加简洁，透彻，尤其在解决椭圆的某些综合问题时，可以利用伸缩变换的办法，把椭圆变换为圆，再利用圆良好的几何性质来进行研究，会使得问题的解决过程变得简化．在利用伸缩变换解决相关问题时，主要利用以下几个性质：

性质1 直线与曲线的位置关系保持不变；

性质3 若直线l和直线m平行，则变换后的直线l′与直线m′仍然平行；

性质5 设ΔABC在变换后变成ΔA′B′C′，则SΔA′B′C′=λμSΔABC．

一、利用伸缩变换研究直线与曲线的位置关系问题

(1)求椭圆C1的方程；

(2)若动点P(x0,y0)为椭圆外一点，且点P到椭圆的两条切线相互垂直，求点P的轨迹方程.

分析：求动点的轨迹方程，通法是设出动点P的坐标P(x0,y0)，寻求x0与y0之间的关系式．本题(2)问抓住直线和椭圆相切这个条件，先利用点斜式(先研究切线斜率存在的情形，再将斜率不存在的特殊情形补充说明)设出直线方程，然后把它和椭圆方程联立，利用方程有等根建立x0、y0与k之间的关系式，最后整理成关于k的方程．因为两条切线垂直，由韦达定理可得k1k2=-1，从而可求得动点的轨迹方程．

说明：遇到直线和椭圆相切的问题时，基本思路是将切线方程和椭圆方程联立组成方程组，利用判别式△=0处理.而利用伸缩变换，可将问题转化为研究直线和圆相切的问题，利用几何法圆心到切线的距离等于半径处理，有效地避免直线和椭圆联立消元的复杂运算，简化了运算过程，给人以一种“拨开云雾见月明”的感觉．本题实际上是一个“蒙日圆”问题，有兴趣的同学可以把这个问题推广到一般情形，动点P的轨迹方程为x2+y2=a2.

二、利用伸缩变换处理弦长问题

例2 如图1，已知椭圆C1的中心在原点O，长轴左、右端点M，N在x轴上，椭圆C2的短轴为MN，且C1,C2的离心率都为e，直线l⊥MN，l与C1交于两点，与C2交于两点，这四点按纵坐标从大到小依次为A,B,C,D．

(2)当e变化时，是否存在直线l，使得BO∥AN，并说明理由．

图1 图2

分析：本题(1)问设出直线l的方程，代入椭圆C1,C2的方程，求出点A,B的纵坐标即可；(2)问可先把直线和椭圆方程联立，表征出点A,B坐标，根据直线平行斜率相等，建立离心率这个目标，通过研究函数的值域求解．

说明：本题(2)问若用传统解法虽然目标很明确，直线平行斜率相等，但点A，B坐标的表征较为复杂，导致离心率的建构不够清晰，进而使得问题的解决困难重重．而通过伸缩变换将椭圆化为圆以后，点A，B重合在同一个圆上，使得坐标表征更为简洁方便，目标的建构也更为清晰．

三、利用伸缩变换研究面积问题

图3 图4

说明：凡涉及到直线与椭圆相交的问题，均可将椭圆通过伸缩变换化为圆，从而转为研究直线与圆的相交问题，进一步利用圆良好的几何特性，达到事半功倍的效果．

四、利用伸缩变换处理垂直问题

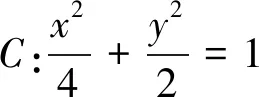
(1)当直线PA平分线段MN时，求k的值；

(2)当k=2时，求点P到直线AB的距离d；

(3)对任意k>0，求证：PA⊥PB.

图5 图6

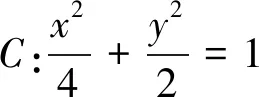
说明：要证椭圆中PA⊥PB，只需探究它们斜率之间的关系，而其中PB的斜率比较难求，将椭圆变换为圆后，可探究圆中P1A1、P1B1之间斜率的关系．在圆中直径所对的圆周角为π，可利用A1B1的斜率很快求出P1B1的斜率，从而问题得到简化与解决．

从以上的例题可知，椭圆中的定点、定值、垂直、弦长、面积等问题，可以先在圆上进行研究，得到一个正确的结论后，再通过变换得到椭圆上与之相对应的结论．或将圆的一些熟知的结论类比到椭圆上，再进行深入的研究，得到椭圆的一个正确的结论，然后进行加工、改编，形成一道适合学生进行知识巩固、方法训练、能力测试、选拔考试的试题．这也是命题中常用的一种有效方法之一．