基于Spark的并行频繁项集挖掘算法
2019-04-01张素琪孙云飞武君艳顾军华
张素琪 孙云飞 武君艳 顾军华
1(天津商业大学信息工程学院 天津 300134)2(河北工业大学人工智能与数据科学学院 天津 300401)3(河北省大数据计算重点实验室 天津 300401)
0 引 言
随着人工智能时代的到来,基于大数据的关联规则挖掘成为国内外科学家研究的热点方向之一,其主要任务是挖掘大数据集中潜在有用的关联关系以及动态数据中规则的变化规律,在很多行业和领域有重要的研究意义和应用前景。随着数据的爆炸式增长,数据集中的关联关系越来越复杂、越来越广泛,关联规则发现的复杂性和实时性需求日益强烈。频繁项集挖掘是关联规则挖掘的第一步也是最重要的一步。Apriori算法是挖掘频繁项集最有影响和最具有代表性的一种算法,但该算法多次扫描数据库,并且产生大量的候选集[1]。基于此,Han等[2]提出了一种不产生候选项集的FP-Growth算法,并且只对数据库进行两次扫描,使得挖掘效率以及空间复杂度方面均有很大改进。随着计算规模不断增大,串行FP-Growth算法会因硬件资源的限制遇到内存瓶颈或者失效的问题[3]。基于分布式计算框架的大数据平台成为解决这一问题的一个重要途径。这些大数据平台在处理海量数据时通过分布式计算框架可以明显提高算法的处理效率,能更高效地引导人们发现潜在的、有利用价值的信息。
基于MapReduce计算框架的Hadoop大数据平台,是一种用于分布式并行环境中处理大规模数据的计算模型[4]。2008年,Li等[5]提出了基于MapReduce的并行化FP-Growth算法——PFP(Parallel FP-Growth)算法,实验证明该算法的挖掘效率呈线性增长趋势并且有良好的扩展性,但是算法并未对FP-Tree挖掘以及负载均衡做出优化。2014年,章志刚等[6]对频繁项目集重新计算支持度的FPPM算法,并在Hadoop平台上加以实现,实验证明该算法能通过减少网络通信量来提高频繁项集挖掘效率。2015年,马强等[7]在FP-Tree节点中新增一个带频繁项前缀的域空间来构建一棵新的NFP-Tree,并在Hadoop平台进行验证与分析,实验证明该算法效率将频繁项集挖掘算法平均提高16.6%。这两种算法都是对FP-Growth算法本身进行改进并在Hadoop上实现,并未考虑在并行实现方式进行改进。2016年,朱文飞等[4]提出基于Hadoop的数据分割以及均衡分组的HBFP算法,实验证明该算法比PFP算法效率提高了约12%。尽管基于Hadoop大数据平台的改进方法在一定程度上提高了FP-Growth算法频繁项集挖掘效率,但是MapReduce编程模型中将各个步骤的中间结果存储到硬盘中,在处理大规模数据时会频繁读取硬盘内容,从而造成挖掘效率降低的问题。相比于Hadoop平台,Spark大数据平台是基于RDD(弹性分布式数据集)的编程框架。Spark相比MapReduce框架的优越性主要体现在两点:第一,Spark将所有运行中间结果均存储在内存中,减少I/O负载,因而更适合迭代运算;第二,Spark丰富的算子使得通过编程实现算法有了更多的灵活性。2015年,Deng等[8]提出了一种基于Spark框架的改进FP-Growth算法—DFP算法,在链头表结构中加入一张哈希表从而快速访问地址,实验证明DFP算法更高效。2016年,方向等[9]提出了基于Spark的均衡分组思想的改进算法—IPFP-Growth算法,实验证明优化后的算法要比PFP效率更高。2017年,张稳等[10]提出一种基于项间联通权重矩阵的负载平衡CWBPFP算法,实验证明该算法高效并有良好的可扩展性。2017年,陆可等[11]基于Spark框架通过支持度计数和分组过程对FP-Growth算法进行改进,实验证明经优化后的算法在面向大规模数据时要优于传统FP-Growth算法。
综上,基于Hadoop的FP-Growth算法改进方法主要体现在FP-Tree挖掘方式和并行化实现两个方面;基于Spark的FP-Growth算法改进主要集中在优化链头表结构和优化分组策略两方面。尽管已经有对Spark的并行化FP-Growth进行优化的算法,但是在优化分组时,仅考虑计算量对挖掘效率的影响,而并未考虑空间复杂度问题。所以,本文提出了改进算法——SPFPG算法:通过综合考虑计算量和FP-Tree规模两种因素对分组策略进行优化,并且运用Spark中丰富的算子对优化算法进行实现。
1 FP-Growth算法描述
FP-Growth是对Apriori算法的改进算法,算法使用一棵FP-Tree存储数据库中的事务,在不产生候选项集的基础上生成频繁项集。FP-Growth算法采用递归策略,并且在整个挖掘过程中,只对数据库进行两次扫描。FP-Growth算法对频繁项集的挖掘过程分为两步:第一步,构造一棵FP-Tree;第二步,对FP-Tree递归挖掘找出所有的频繁项集。
1.1 构建FP-Tree
(1) 第一次扫描数据库D,计算出所有项支持度计数,找出满足最小支持度的项并把这些项按支持度递减排序,生成频繁1-项集列表—F-List。
(2) 更新数据库D:将数据集中每条事务中的项按照F-List中项的顺序进行排序,删除不满足最小支持度的项,即数据库更新后每条事务中的项都满足最小支持度且都按照支持度降序排列。
(3) 第二次扫描数据库D,根据D中每条事务出现的频繁项顺序构造一棵FP-Tree。创建树的根节点null,并将每条事务中的项添加到FP-Tree的一个分支。为了更有效率地遍历FP-Tree,创建列表包含所有头节点,表中每个元素为F-List中的元素,每个元素通过一个节点链指向它在FP-Tree中出现的位置。
1.2 FP-Tree挖掘
FP-Tree的挖掘采用自底向上的递归思想,如果路径中包含头结点列表中元素,那么该元素的指针会指向路径中该元素的位置;然后基于这些路径构造该元素的条件模式基;最后对条件模式基进行递归挖掘找出含该元素的所有频繁项集。对头节点列表中所有元素自底向上都执行以上的操作,最终挖掘出所有频繁项集。
1.3 FP-Growth算法挖掘实例
事务数据库D如表1所示,最小支持度0.6。

表1 事务数据库D
算法挖掘流程如下:
(1) 对D进行第一次扫描,生成的F-List列表为<(n:5),(m:4),(o:3),(p:3)>,更新后的数据库列表如表2所示。
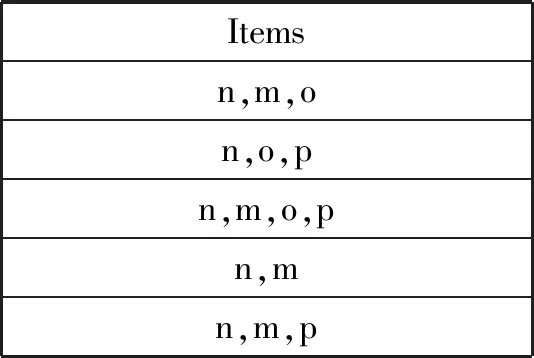
表2 更新后的事务数据库
(2)对D进行第二次扫描,生成FP-Tree以及头结点列表,如图1所示。
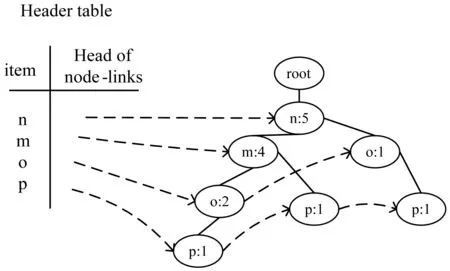
图1 生成的FP-Tree
(3) 对FP-Tree递归挖掘得到的频繁项集如表3所示。

表3 递归挖掘得到的所有频繁项集
2 基于Spark的FP-Growth算法实现
当数据集规模很大时,串行FP-Growth算法构建的FP-Tree横向或纵向维度变得很大,存储FP-Tree会造成失败;同时由于挖掘过程中的递归次数增加,造成挖掘效率变得极低[12]。所以基于Spark的并行FP-Growth算法—SFPG算法思想是将原始数据库划分到不同的节点,然后通过构建局部FP-Tree对各个节点的频繁项集进行挖掘,最后合并得到全局频繁项集[13]。
SFPG算法在Spark上的并行实现主要分为四个步骤:步骤一,读取原始数据库,对数据库进行更新并且产生F-List;步骤二,对数据库进行分组,按照一定规则将数据库中的每条事务划分到不同的Partion中;步骤三,对每个Partion用FP-Growth算法进行频繁项集的挖掘;步骤四,将步骤三中的每一个分组中的频繁项集挖掘结果进行合并,得到整个数据库的挖掘结果并将结果输出到HDFS上。算法主要实现过程如图2所示。

图2 SFPG算法流程图
步骤一中,要将原始事务数据库分布到RDD上,然后并行进行不同项的支持度计数统计。首先对挖掘任务初始化,再遍历每一条事务,对不同项进行支持度计数统计并按照从大到小排序,最后将所有满足最小支持度的项进行结果合并然后保存在内存中,得到F-List,同时对数据库进行更新,即删除每条事务中不满足支持度的项并按照支持度计数进行排序。
步骤二中,对更新后的数据库进行分组,首先将F-List划分为g个分组,生成group-list,这个列表中的元素包括item以及该项对应的group-id,然后将数据库中的每条事务根据group-list列表划分到不同的分区中。在划分之后得到Group-list,其存储分区号和划分到该分区的分事务组以及各个事务出现的次数。数据库进行划分采用将相同group-id的分事务分布到相同分组的方法,实现在后续进行频繁项集挖掘的过程中挖掘结果的完整性和准确性。
步骤三中,对划分到每个分区的分事务进行频繁项集挖掘,实现并行化挖掘。在本步骤中,每个分组只对划分到该分区的事务组包含的项进行逐项遍历,这样避免了频繁项集的重复挖掘。
步骤四中,将所有频繁项集进行合并,并将结果转换成所需格式。
3 基于Spark的FP-Growth优化算法——SPFPG算法
在第2节的叙述中可以看出,步骤二对整个并行算法执行效率起着关键作用。在这一步骤中执行对F-List进行分组操作以及数据库的划分操作。本文对算法的改进主要体现在分组策略的优化,并且运用了Spark丰富的算子对优化算法进行实现。
F-List分组作为整个并行挖掘的一个重要环节,为了使每个分区的挖掘任务均衡,应该改进对F-List的分组策略。由于在对频繁项集进行并行挖掘的时间取决于最后一个分区完成的时间,所以在进行分组时应该尽量使每个分区的挖掘时间相等。基于MapReduce编程框架的PFP算法采用的分组策略并未考虑负载均衡问题,在集群进行频繁模式挖掘任务时,会造成节点与节点挖掘负载相差很大。PFP算法分组策略:首先根据F-List中的元素个数和分组数g求出划分到每个组的最小元素个数为items_num,然后对已经按照支持度降序的F-List从后向前遍历,将其中(i%items_num+1)到(i+1)×items_num(i:0~g-1)的项划分到第i组。根据第1节中介绍,在构建FP-Tree时,从根节点到叶子节点支持度逐渐降低。由于支持度越低时,根据该项构建的条件模式树越高,递归次数越多,相应的挖掘任务负载越大,而在PFP算法中将支持度相对较大的项和支持度相对较小的项划分到不同组中,会造成不同分组之间的挖掘时间有很大差别,故造成负载不均衡。
已有的优化算法在分组策略上的改进主要是根据不同分组的计算量,关注点在时间复杂度。本文增加FP-Tree规模这一参考标准,即考虑各个分组中FP-Tree的横向或纵向维度。通过综合考虑时间复杂度和空间复杂度,得出负载均衡的分组策略,从而更好地实现分组。具体求出不同分组的计算量非常复杂,但是基于上段的分析,计算量主要体现在不同项所处路径的长度,而这是由该项item在F-List列表中具体位置决定的,据此对分区挖掘频繁项集计算量CAL进行估计:
CAL=lg(L(item,F-List))
(1)
FP-Tree规模是由项在F-List中的位置和该项的支持度计数进行度量。假设项的支持度计数为sup,项在F-List中的位置为loc。FP-Tree的规模可作如下估计:
Size=sup×(loc+1)/2
(2)
其中,sup越大,对应的loc也越大,即这两个变量有相同的变化趋势,所以可以得出树的规模Size主要由loc决定。在确定了两个度量标准之后,可以将分组策略优化示意图表示出来,如图3所示。假设F-List中元素个数items=18、g=6,图3中横轴代表项item在F-List列表中的位置,(a)中实线和虚线分别代表未优化分组时的计算量和FP-Tree规模,优化分组之后如(b)所示。
虚线a与经过对称变换的曲线的交点所对应原曲线的x轴坐标,即为优化之后的每个分组中的元素。采用这样的划分可以保证在某一时刻总是将较大计算量和局部FP-Tree规模较大的那个后缀模式项放在计算量和局部FP-Tree较小的那个分组,保证让组内的计算量和FP-Tree存储规模大致相同,实现负载均衡。
假设F-List中的频繁项个数为9,分别用9、8、7、6、5、4、3、2、1(用数字代表支持度的降序排列)表示,分组个数为3。未优化的分组策略示意图如图4所示。

图4 未优化分组结果示意图
从图4可以看出,第1组负载最高,第3组负载最低,造成挖掘任务负载不均衡从而影响挖掘效率。按照本文提出的优化策略的分组示意图如图5所示。

图5 优化分组结果示意图
从图5可以看出,优化分组策略使得剩余频繁项中负载最大的项划分到当前分组中负载最小的分组中,达到组与组之间的负载均衡。
4 实验结果分析
为了验证本文所提出的SPFPG算法的有效性,实验选取数据集retail.dat,该数据集取自Frequent ItemSet Mining DataSet Repository[14],该网站提供的数据集常用于频繁项集的研究。webdocs.dat数据集大小为1.48 GB,有1 692 082条事务和一共5 267 656个属性。从webdocs.dat数据集中随机选取事务生成五个测试数据集,记为{D1,D2,D3,D4,D5},每个数据集中事务数依次为10万条、20万条、30万条、40万条、50万条。
实验所用Spark集群由三个节点构成:一个主节点和三个从节点(其中一个节点既是主节点也是从节点),每个节点的配置为:CPU核数为4,内存为8 GB,操作系统Centos 6.8,Hadoop版本为hadoop-2.6.2,Spark版本为spark-1.6.1-bin-hadoop2.6.2,JDK版本为JDK 1.7.0_79,Scala版本为 Uscala-2.10.5。实验分别比较了数据量、集群节点个数对SFPG以及SPFPG算法挖掘效率的影响,同时对SPFPG算法有效性进行了验证。
4.1 挖掘时间与数据量之间的关系
本文设置支持度为20%。首先用未优化的基于Spark的FP-Growth算法对六个测试数据集进行频繁项集挖掘,然后再用本文提出的SPFPG算法对测试数据集分别进行频繁项集的挖掘,最后对两个算法的运行时间进行比较。实验结果如图6所示。

图6 webdocs.dat数据集实验结果
图6中横坐标表示事务数大小,纵坐标表示算法运行时间,两条曲线分别表示两个算法运行时间的变化趋势。从图6可以看出,当事务数据量不大时,优化前后的算法挖掘时间相差不大,SPFPG算法并没有体现出明显优势。随着数据量的不断增大,可以看出SPFPG算法挖掘效率要明显高于SPFG算法。实验说明,面对海量数据集,SPFPG算法更有利于提高频繁模式挖掘效率。
4.2 挖掘时间与集群节点个数之间的关系
针对webdocs.dat数据集,在支持度保持不变条件下,集群节点数从1递增到3,通过SFPG算法和SPFPG算法对数据集中频繁项集进行挖掘。实验结果如图7所示。

图7 挖掘时间与集群节点个数关系图
图7中横坐标表示集群中的节点个数,纵坐标表示算法运行时间,曲线分别表示两种算法运行时间的变化趋势。从图7可以看出,随着Spark集群节点数的增加,SFPG和SPFPG算法对频繁项集挖掘时间都会减少,但SPFPG算法效率优势更明显,说明本文提出的分组策略能大大提高挖掘效率。
4.3 算法有效性验证
通过改变实验数据集的大小,分析Spark平台在不同节点数目下SPFPG算法所需的时间,计算加速比来验证算法的并行性。加速比的公式如下:
(3)
式中:Sp代表算法加速比,t为使用1个节点时实验执行的时间,tp为使用p个节点时实验执行的时间。
SPFPG算法在两个测试数据集D3和D5上不同节点个数情况下的加速比如图8所示。图8中横坐标表示集群中节点个数,纵坐标表示加速比,两条曲线分别表示不同数据集对应的加速比变化趋势。从图中可以看出,在两个不同数据集下,算法加速比与节点数目的增加近似成正比的关系。可见,SPFPG算法处理数据集具有较好的并行性。
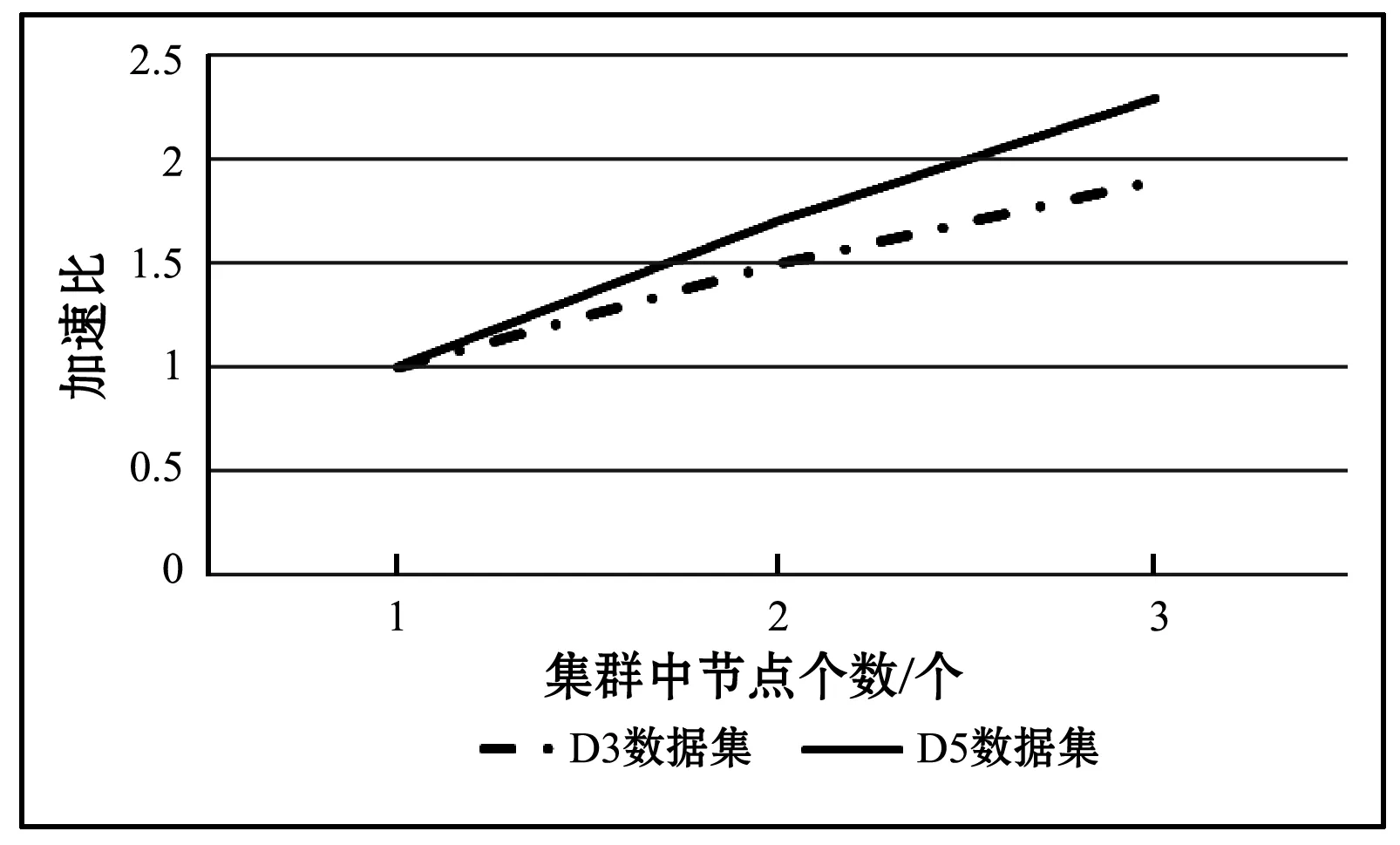
图8 SPFPG算法加速比
5 结 语
为了解决Spark下频繁项集挖掘过程中的分组不均衡问题,本文提出基于Spark的SPFPG算法。该算法在进行分组时,通过综合考虑不同节点的计算量和FP-Tree规模来实现均衡分组。实验结果表明,SPFPG算法提高了频繁项集的挖掘效率,且算法具有良好的并行性和扩展性。
