基于学习排序的多分类标签排序方法研究

贺成诚 汪海涛 姜 瑛 陈 星

(昆明理工大学信息工程与自动化学院 云南 昆明 650500)

0 引 言

学习排序作为计算机领域内相对较新的研究领域，在我国发展迅速。在包括信息检索、数据挖掘、自然语言处理及语音识别[1]等在内的多个领域内均发挥着重要作用。在学习排序的相关问题中，一个实例是一组对象而标签是应用于对象的排序列表。特别是学习排序旨在从训练实例和排名标签构建排名功能。通常每个标签都假定为客观且可靠的，可用于其他常规监督设置，例如分类。因此标签排序的问题可以被认为是传统分类的一般化，将完整的标签排序作为预测而不仅仅是一个类别的标签。

现有的标签排序方法主要是将原始学习问题转化为一个或多个二元分类问题的归约技术。例如，约束分类，即将原始问题转化为高维扩展空间中的单一二元分类问题，并利用该空间学习的分类器构件标签排序模型[2]。此外，也存在通过将原始问题拆解成多个小问题，利用每对标签学习一个二元模型并最终合并所有预测结果的方法来解决传统的二元分类问题[3]。这种缩减技术在本文的实验研究中具有较好表现。值得注意的是，它使标签排序问题适用于(二元)分类方法和现有算法在这一领域的大量库，将标签排序问题简化为二元分类的简单问题能更好地解决实验问题。但是，将多个二元模型预测结果还原到原有问题的还原技术也存在一些问题。首先，“排序值”映射的理论假设可能不适合作为适当的学习偏见，并且可能不容易转化为分类问题的相应假设。其次，二元问题最小化分类错误或相关损失函数通常并不清楚。在排序上等价于根据期望损失函数最大化标签排序模型的(预期)性能[4]。本文针对以上两个问题，采用所有排序类别的参数化(条件)概率分布进行标签排序的方法进行代替，从而将学习问题转化为最大似然估计的问题(或者作为贝叶斯推理的问题)进行研究。

1.3.1 血压水平 采用血压计测量治疗前后两组妊娠期高血压疾病患者的收缩压(SBP)和舒张压(DBP)。

Cheng W等[5]提出使用Mallows模型并开发了一种基于实例的(最近邻居)学习算法来以局部方式估计该模型。Cheng W等[6]提出了将Plackett-Luce(P-L)模型用于标签排序的方法，该模型更倾向于从可能不完整的标签排名中进行学习。

该项研究结合了两个经典的模型，即Plackett-Luce(P-L)模型和广义线性模型[7]，构建了一种新的学习排序框架。在这个排名模型中，需要学习排名函数和真实值排名标签。并且在算法中，使用最大化似然估计方法，以迭代的方式推断出最优的排序预测，以及要学习的排序功能的参数。整体流程如图1所示。

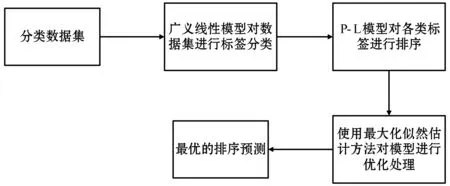
图1 整体流程图

1 标签排序模型

本部分对广义线性模型和P-L模型的定义及特点进行了介绍，并为后续新模型的提出作出说明。

1.1 广义线性模型

广义线性模型是典型的线性模型的推广。它通常用于分析事物之间的统计关系，并侧重于考察变量之间的数量变化规律。而在实际应用中，广义线性模型可以用来解决多类别的分类问题。比如在分类和回归问题中，我们通过广义线性模型来预测两个相关变量之间的数量关系等。

2015年6～8月，正值药品稽查“农忙时节”，因丈夫被公派出国留学，黄梅不得不一边工作，一边独自带着1岁的女儿担起家庭重任。在此期间，她参与了“幸福伤风咳嗽”假药案、“小儿健胃宝”假药案、“公牛牌超速效鼻炎灵”假药案、“板蓝根冲剂”假药案等系列假药案的查处。案件数量多、案情复杂，加班成为常态，她常常不得不把年幼的女儿托付给自己年迈的母亲。

广义线性模型三个前提假设分别如下：

(1) (y|x;θ)是一个以θ为参数的指数分布。

(2) 给定x的情况下的目标函数为h(x)=E[T(y)|x]。考虑到大多数情况下T(y)=y，即目标函数可以表示为h(x)=E[y|x]。

(3) 假设自然参数η和x为线性关系，即假设：η=θTx。

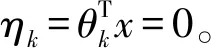
2)比较两种函数的运算结果，发现conv()输出长度为 6 的序列[3，5，11，17，8，16]，filter()输出长度为 4 的序列[3，5，11，17]，但两个序列的前 4 个元素相同。

(1)

式(1)为在y=i时的概率分布。由前提条件式(2)可知在这个广义线性模型中，目标函数为：

hθ(x)=E[T(y)|x;θ]

(2)

通过在式(2)的基础上构造分类模型并利用相关数据来求解目标函数hθ(x)，并结合参数拟合与梯度下降的方法求解原模型。

1.2 P-L模型

P-L模型是一种典型的基于分数的模型，它通常用于列表学习排序中。其中P-L模型中的假设条件是式(3)中的评分向量，而不是等级和固定参数。P-L模型由分数向量v=(v1,v2,…,vM)来参数化，其中vi(>0)与索引i相关联，计算给定一个分数向量的排名π的概率。

(3)

式中:(T(y))i表示T(y)的第i个元素。

(4)

显然，与vb相比，va越大，选择a的概率就越高。同样，式(3)中的参数vi与参数vj，j不等于i且相比越大，标签yi出现在最高等级上的概率越高。P-L模型可以用一个花瓶模型来直观解释：如果vi对应于充满标记球的花瓶中的第i个标签的相对频率，则p(π|v)是通过随机从花瓶中依次抽出球，并将第k个试验中的标签绘制在位置k上(除非之前已经选择了标签，在这种情况下，试验被取消)，从而产生排名π。

（2）树立人本理念。在新的经济环境中，不能忽视经济一体化以及全球化的趋势和特点，不能故步自封、因循守旧，应该结合房钱的网络信息技术、科学财务管理工具及方法等，推行科学、高校、人性化的财务管理理念，重视对财务工作人员的综合素质培养。

The purpose/aim/objective of this study/paper/research was/is to…

对于P-L模型，可以用式(3)验证不完全排名yπx(1)≻xyπx(2)≻…≻xyπx(k)(yπx(i)≻xyπx(j)表示相较于yπx(j)实例x更偏向于yπx(i))。即在完全相同的形式表达下，因子的数量k(观察到的标记的数量)是影响其概率分布的唯一要素。如下式给出：

(5)

2 基于实例的标签排序

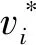
2.1 标签分类

考虑到实际生活中存在较多种类的标签，因此本文首先利用广义线性模型对多类别标签的分类问题进行分析。

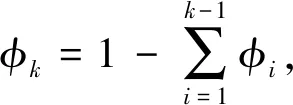
(6)

该模型是布拉德利特里模型的一种推广，是用于替代成对比较的模型，它指定了“a优于b”的概率(a≻b表示a先于b)的概率，公式如下：

为了表示方便，我们用符号1{·}表示判断，{}中的表达式为真时输出1，为假时输出0。于是有(T(y))i=1{y}(i)，它表示只有当y=i时(T(y))i才不会为零。另外，由于φi表示第i个类别的概率，则有E[(T(y))i]=p(y=i)=φi。

由于此分布属于指数分布族，故设该分布的标准参数为η，ηi表示第i维的标准参数，定义为：

到2016年，全市一级河道Ⅴ类以上水体达到60%，二级河道Ⅴ类以上水体达到50%，显著提升水生态环境质量。2014年清水河道行动计划实施七大类1311项工程。截至6月27日,完工433项,完工率33.8%,开工在建388项。

(7)

根据式(7)，可得到：

(8)

设θ≥0是扩展参数，且(y|x;θ)属于指数分布族，根据广义线性模型的第三个前提假设条件η=θTx，由式(8)可得：

定理 2.1[8] 令→是[0,1]上的正则蕴涵算子。若→满足:对任意的a,[0,1], a+a→b≤1+b,则

(9)

最后利用梯度下降法来求出使似然函数最大的θ值。

(10)

之后使用最大似然的方法来学习θ，似然函数为:

(11)

根据目标函数式(2)求解目标函数，构造出分类模型：

(12)

令式(12)等于0，求出θ的最优解。最后利用此最优θ求出此标签的最佳分类。

2.2 各类标签排序

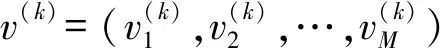
(13)

v的最大似然估计由最大化该概率的参数给出，或者等效为对数似然函数。MM算法[8]作为一种迭代算法，通过每次迭代中最大化一个函数直至将原始函数进行求解的方式可以很好地用于求解：

(14)

假设φ上的概率分布p(·|x)至少近似地在查询x。进一步假设排名πi是通过P-L模型式(5)彼此独立产生的，则观察排名π={π1,π2,…,πK)}在给定参数v=(v1,v2,…,vM)的情况下变为:

给定最大化估计v*，可以从φ上的分布p(·|v*)推导与x关联的排名的预测。由下式确定具有最高后验概率的排序：

(15)

式中：τ是一个Kendall的常用度量，定义为：

vπ*(i)≥vπ*(j)

(16)

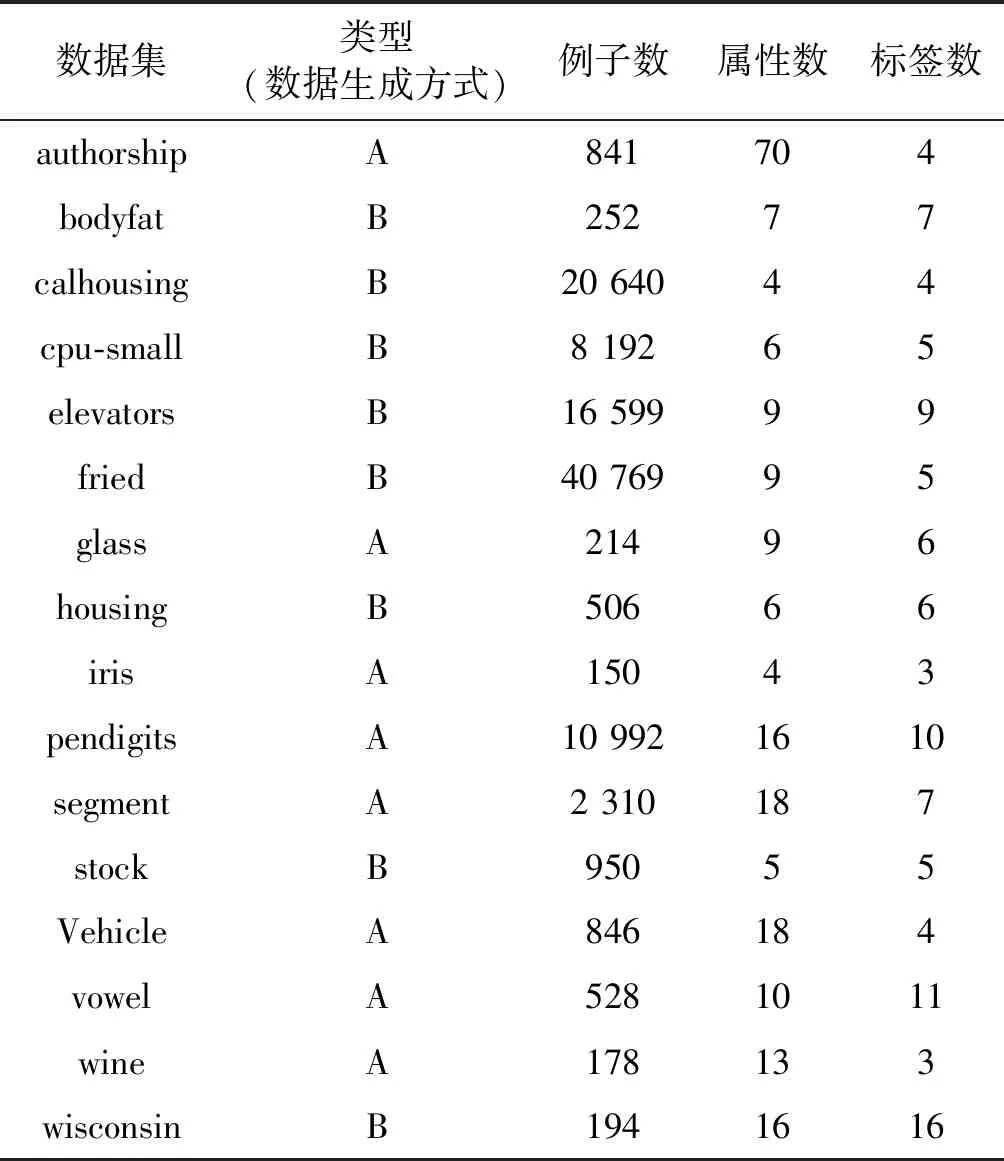
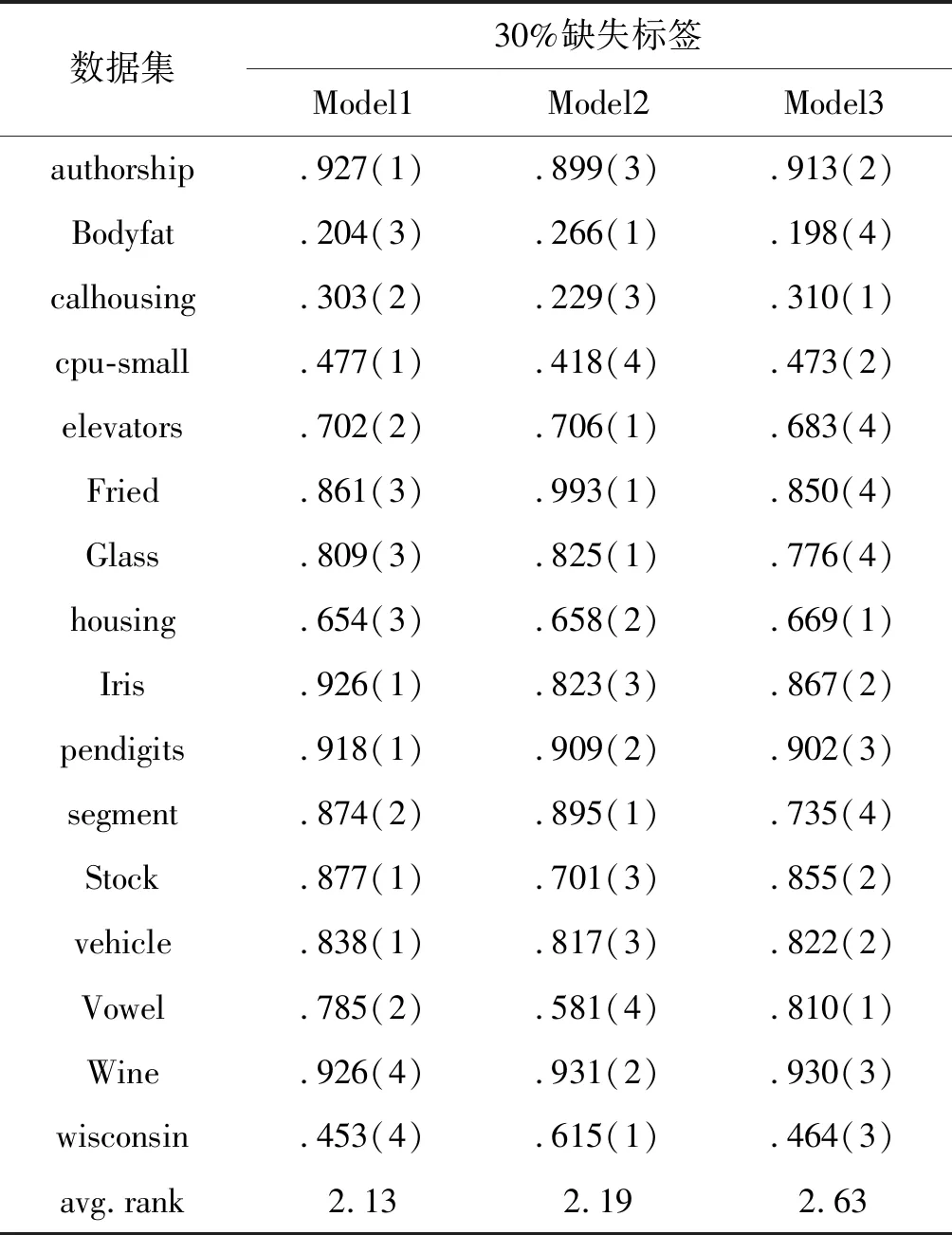
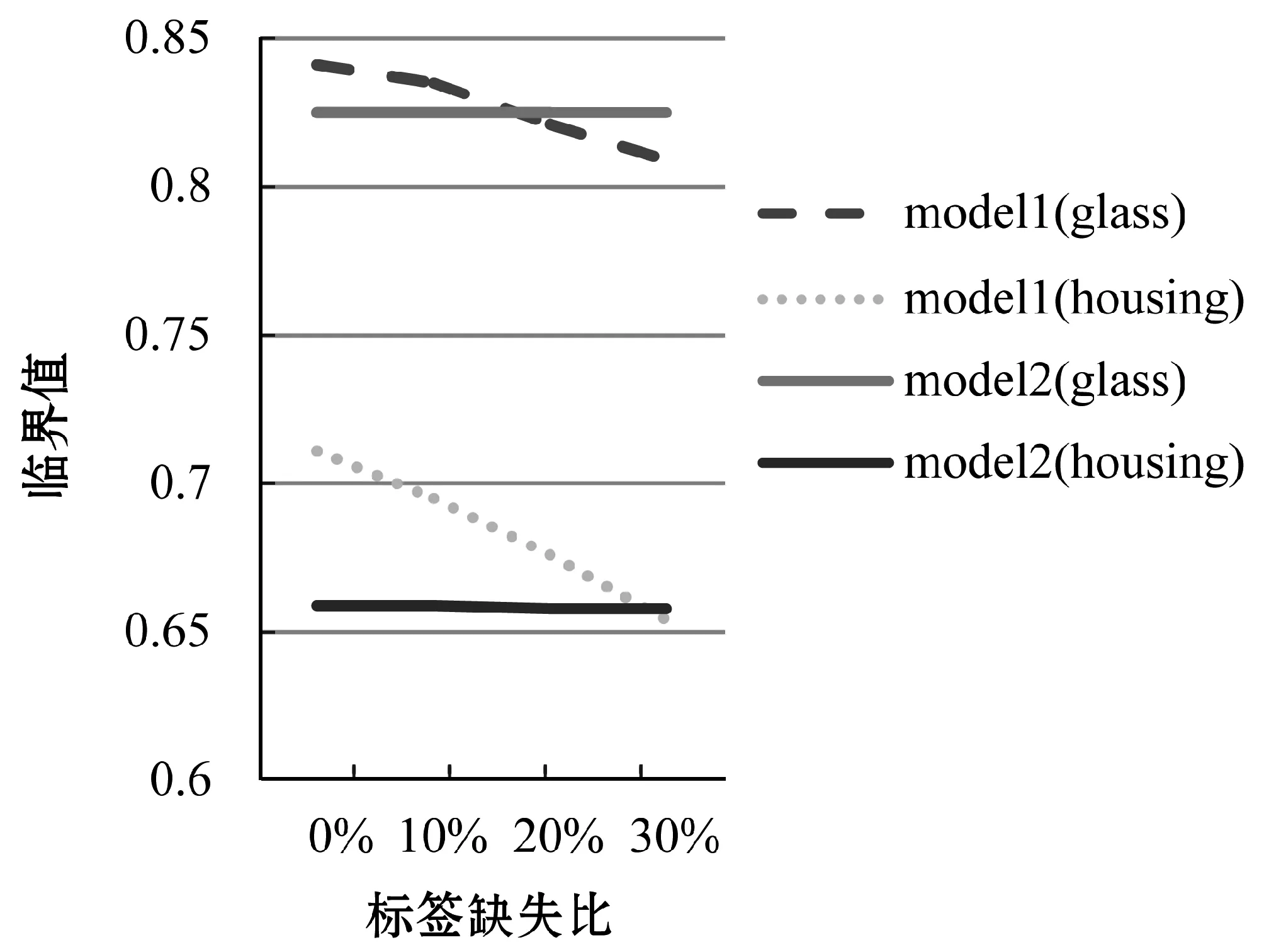
对于所有的1≤i

(17)

强生公司从全部召回的3500万瓶泰诺速效胶囊中，发现8瓶含有氰化物。这8瓶胶囊均来自于芝加哥地区。警方推断凶手是在药店买了胶囊后，把胶囊拆开混入毒物后重新装好，再偷偷放回货架的。

(18)

式中：C(π,σ)表示π和σ中一致对的数量；D(π,σ)表示π和σ中不一致对的数量。

本文用于在各类标签中预测最优的标签排序算法步骤如算法1所示。与简单地根据排名产生预测的其他方法(包括大多数简化技术)相比，本文的排序模型的概率方法允许通过不同类型的统计信息来补充预测，例如预测的可靠性等，并且能解决多分类标签的排序问题。此外，分布p(·|v*)支持包括可靠的排序集覆盖真实的高概率问题在内的多种类型的广义预测。

算法1各类最优预测标签排序算法步骤

输入：θ

广州中海达卫星导航技术股份有限公司……………………………………… （2、4、6、10、12、16、18、22）

输出：v*，π*

步骤：

1. 根据广义线性模型求出的标签最佳分类θ获得每个类的标签排序集π。

2. 为每个π选择标签集中的最大元素v*。

标准化实验教学课程大纲应包括课程信息、课程目的、教学要求、教学内容(含课外教学)、考核说明及课程教学评价、课程持续改进、教学参考书等。目前，很多高校采用优、良、中、及格和不及格5个等级评价实验教学成绩，缺乏相应的教学评价量化标准。因此，教学大纲的标准化不因开课学校和开课教师而发生变化，将有效地规范课程教学，这样更有利于知识的精准传授。标准化实验教学大纲的构建可以借鉴针对专业核心课程大纲的标准化建设[7]，其中实验课程的教学要求和课程评价是标准化实验教学大纲中十分重要的内容。笔者以湖北大学制药工程专业药物化学实验教学大纲中的考核说明及课程教学评价为例说明。

3. 使用最大似然估计更新π以得到最优预测排序π*。

3 实 验

3.1 数据准备

本文采用UCI存储库和Statlog集合的分类数据集及回归数据集，并以两种不同的方式将它们转换为标签排名数据：(1) 本文首先利用广义线性模型对分类数据进行训练，之后将所得每个示例数据集中存在的所有标签相对于预测类别概率进行排序，其中在关系情况，具有较低索引的标签排在第一；(2) 对于回归数据，本文首先将预测变量组中数据属性予以删除，并将每个属性均视为一个标签，之后本文将属性进行标准化，并按大小顺序进行排序以获得排名。表1给出了数据集及其属性的总结。

表1 数据集及其属性

3.2 实验设计

我们将使用基于实例的广义线性模型和P-L模型结合的方法(model1)和广义线性模型方法(model2)、基于实例的Mallows(model3)模型方法进行标签排序的实例评估。

为了保证实验公平，本文在归一化属性之后使用欧几里德距离[9]作为实例空间上的P-L模型和Mallows模型的距离度量。通过训练集上的交叉验证选择邻域大小K∈{5,10,15,20}。

本项目随机选择多发、单发内膜下、肌层及浆膜下子宫肌瘤病例150例，同时取对应的子宫肌层组织作为对照，所有标本均采用4%甲醛固定，石蜡包埋、HE染色。采用免疫组化法（SP），切片厚 4 μm，切白片 3张，高温修复或酶消化，4℃冰箱过夜，以PBS缓冲液代替第一抗体作为阴性对照，已知的阳性组织作为阳性对照。免疫组化试剂ER、PR、WT-1及SP试剂盒购自迈新公司，操作按试剂盒说明书要求进行。

本文利用Kendall的tau系数的10次交叉验证，并重复5次实验后得出实验结果。同时，为了模拟不完整的观察结果，本文对数据进行了如下修改：对于排名中的每个标签，有偏见的硬币被翻转以决定是否保留或删除;其中，删除的概率由参数p∈[0,1]指定。因此，平均丢失的标签数为p×100%。

看到过“鲲龙”AG-600本尊的人，往往都会产生一种“诡异”的感觉。那是因为相对于一般飞机的流线型机身来说，它的飞机船身采用了大长宽比的设计，让人感觉很不协调。实际上，不论是哪一种能够在水面起飞的飞机，都会面临在水面滑行过程中出现的不可控制的“海豚运动”、弹跳、摇摆等情况。“鲲龙”AG-600采用大长宽比设计的目的，就是为了最大限度地减少降落时水面载荷对船身的冲击，以及提高在水面滑行时飞机的纵向稳定性。

3.3 实验结果及分析

实验结果总结如表2、表3所示。本文按照Demsar.J.于2006年推荐的两步程序[10]进行结果分析。首先对结果进行对零假设的Friedman检验[11]，即判断所有学习者都有相同的表现。当该假设被拒绝时采用Nemenyi测试[11]以成对的方式比较学习者。这两项测试均基于平均等级(对于每个问题，方法按性能降序排列，并且由此获得的等级针对问题进行平均)，如表2、表3中的最后一行所示。从表2中可以看出Model1和Model3在完全标签的情况下优于Model2，而Friedman测试在30%缺失标签的情况下，如表3所示Model1与Model2没有显着差异,但Model1明显优于Model3,就总体Model1相比Model2和Model3提高了约5%。

表2 根据Kendall的tau(括号中的等级)完整标签中排序方法的表现

表3 根据Kendall的tau(括号中的等级)缺失30%标签中排序方法的表现

通过对表2和表3的数据进行分析，本文得到了以下结论：

首先根据实验结果发现，在丢失标签信息的情况下，我们提出的新方法比Mallows模型方法准确性提升了约5%。这与我们的预测非常吻合，即在同类标签的排序中P-L模型更适合从不完整的排名数据中学习。

城市在其发展过程中逐渐形成居住区、商业区、工业区等不同功能区[1]。识别城市不同功能区并研究其空间分布特征对研究城市的未来发展、城市的合理布局和城市建设的综合部署有着重要的意义[2，3]。传统的城市功能区识别主要是基于专家评判、调查统计等以经验为主的方法，主观性较强。也有一些学者通过遥感技术辅助实现城市功能区划，但数据获取和处理的成本较高，时效性差[4]。随着信息化时代的到来，可供城市规划相关研究所应用的数据不断涌现，包括传统数据、开放数据等各类大数据资源。在这些数据不断丰富的背景下，基于城市生活数据的功能区分析也变得更加快速、有效[5]。

其次，将广义线性模型和P-L模型结合的方法在完整标签和丢失标签信息的情况下都比单一的广义线性模型表现更好，其中在标签完整的情况下，准确性提升了约5%。

最后，实验结果也证明广义线性模型和P-L模型具有一定的互补性。就像传统分类的情况一样，基于实例的方法对于需要复杂决策边界的问题是有利的，因为线性方法的强偏差妨碍了它们实现良好的分离。另一方面，如果线性假设是(至少近似)有效的，那么可以用更少的数据来学习更好的模型。相应地，基于实例的学习者对于训练数据量更加敏感。一些有利于这一假设的证据的确是通过学习曲线提供的，该曲线将性能描绘为遗漏标签信息的一部分的函数。虽然线性方法的学习曲线通常相当平坦，呈现出一种饱和效应，但对于基于实例的方法而言，它们更陡峭。这表明，即使线性方法由于缺乏灵活性而不再能够利用和适应额外数据，附加标签信息仍然对这些方法有益。玻璃和外壳数据的典型例子如图2所示。

图2 排名表现

4 结 语

本文提出了一种将广义线性模型和P-L模型结合作为底层数据生成过程的新模型方法，并利用实验对比了其与传统的广义线性模型方法及基于实例的Mallows模型的优劣，实验结果显示本文构建的新模型方法在学习排序问题研究方面具有一定的优越性。尤其是在不完全的训练数据情况下，新的模型方法在计算与性能上均有更好的表现。此外，本实验也证明了广义线性模型在处理不同类别标签分类上对P-L模型也提供了一定的补充。

同时，本文的概率模型1采用最大似然估计的方法作为标准拟合模型的补充，减少了模型估计中存在的偏差，一定程度上提高了模型的准确度，更符合模型的前提假设。此外，通过最大似然估计的估计方法也允许实验者通过添加不同类型的统计信息来补充实验预测，使实验更加精准可靠。

虽然本文提出的新模型在一定程度上为研究学习排序提供了新的研究思路与方法，但仍存在一些问题需要解决。例如本文提出的解决多分类标签排序的方法建立在第一部分广义线性模型对标签进行了正确分类的基础上，如果广义线性模型确定的分类结果存在偏差，则整个模型方法的可靠性与精准性均会受到一定程度的影响。针对该问题，拟将本文提出的模型方法进行更深层次地合并，通过类似局部线性回归等方法，放宽原模型中较为严格的假设，从而保证实验的准确与可靠。