基于连边密度传播的二分网络社区发现算法
2019-04-01安晓丹张晓琴曹付元
安晓丹 张晓琴 曹付元
1(山西大学数学科学学院 山西 太原 030006)2(山西财经大学统计学院 山西 太原 030006)3(山西大学计算机与信息技术学院 山西 太原 030006)
0 引 言
自然界有许多复杂网络,如社会网络、技术网络和生物网络等。这些网络大部分都会呈现出社区结构,即社区内部连边分布较密集,社区间的连边分布较分散。社区发现对挖掘复杂网络的结构、预测对象的行为特征、提取网络的有用信息具有重要的研究意义。
网络的一个重要类型是二分网络,现实中许多真实的二分网络,例如用户-产品购买关系网[1-2]、新陈代谢网络[3]和疾病-基因网络[4]等。二分网络可以体现出一些深层网络结构特点,对网络结构特性的研究具有非常重要的作用[5]。
目前,主要有两种二分网络社区划分方法,一种是将其转化到单模网络上进行聚类、分析。如Melamed D[6]的双映射方法,但是这些方法会损失大量的网络信息。为降低映射过程的信息损失,张嫱嫱等[7]对两个网络的资源分布矩阵聚类分析。另外一种是直接在二分网络上进行划分,这些方法可以较有效地保留原网络大部分信息。如Barber等[8]提出的BRIM算法。周旸等[9]针对传统谱方法在二分网络社区发现中的缺点,提出了基于最优特征向量的谱二分社团检测方法。Tang等[10]将谱聚类算法的思想推广到二分网络,提出了联合谱聚类算法。邹凌君等[11]通过构建广义后缀树,提出了一种可以发现重叠社区的社区发现方法。Lehmann等[12]将K-clique算法[13]推广到了二分网络,提出了bi-clique二分网络社区发现算法。bi-clique算法的主要优点是可以发现重叠社区和不同连接密度的社区;缺点是只挖掘了那些密度超过指定阈值的二分网络[14]。
为了度量社区划分结果,Newman[15]提出了适合单模网络的模块度指标,因为该模块度依赖于零模型,因此在一些网络上存在分辨率限制。在二分网络上,Guimera等[16]、Barber[8]和Murata[17]基于Newman的单模网络模块度,提出了二分网络的模块度。虽然二分网络的模块度受到广泛应用,但Xu等[18]和Li等[19]指出以上模块度也存在一定的分辨率限制。
为缓解模块度在某些网络上的分辨率限制和算法精度不高的问题,本文提出一种二分网络评价指标。同时,利用密度传播和最优化评价指标,提出一种可自主识别社区的二分网络发现算法,并通过实验验证该算法的有效性。
1 二分网络的相关介绍
1.1 二分网络的概念
二分网络有两种类型的节点,且只有不同类型节点间有连边。二分网络可以表示为简单无向图G(X,Y,E)。X、Y分别表示二分网络的两类节点,E表示X和Y节点间的连边。
设X型和Y型节点个数分别为m和n,由于X(Y)型节点间没有连边,因此二分网络的邻接矩阵可以表示为:
式中:
0m×m、0n×n分别为m阶、n阶零矩阵;
1.2 二分网络的互信息指标
二分网络的互信息指标[16]被用来比较两种社区划分结果的一致性,假设有两种社区划分C和D,其互信息定义如下:
式中:
M表示网络总连边数;
NC和ND分别为C和D划分的社区个数;

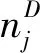

若划分C与D完全一致时,ICD=1;
若划分C与D不相关时,ICD=0。
1.3 Murata的模块度
假设网络的总边数为M,Vl和Vm分别是X和Y型节点的社区(Vl∈VX,Vm∈VY),邻接矩阵A中的元素为aij。连接Vl和Vm的边与网络总边数的比可表示为:
进一步定义矩阵B,B中的元素由elm组成,那么矩阵的第l行所有元素和bl为:
Murata的模块度定义如下:
1.4 Barber的二分网络模块度
鉴于二分网络同类节点间没有连边的特点,Barber将节点xi与xj的连边概率矩阵定义如下:
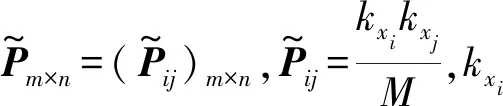
式中:


1.5 BRIM算法
BRIM算法是Barber采用递归的方法得到的社区划分方法,具体如下:

定义指标矩阵:

式中:R、T分别为m×c、n×c的矩阵,c为社区个数。那么,Barber的模块度可写为:

1.6 边集聚算法
Zhang等[20]对聚类系数做了修正,定义了如下的边集聚系数:
式中:m是X型节点i的邻居,n是Y型节点j的邻居。如果邻居m和n相互连接,则qijmn=1,否则为0。θijmn与qijmn相反。km是节点m的度,kn是节点n的度,ki是节点i的度,kj是节点j的度。这个算法如同GN算法[21-22],计算每条边的集聚系数,但是去掉集聚系数最小的边。
1.7 资源分布算法
吴亚晶等[23]提出的资源分布算法,通过构建二分网络的资源分布矩阵,然后对资源分布矩阵进行K均值聚类,并采用F统计量确定最终聚类结果。
2 连边密度传播算法
以往二分网络的模块度是从社区中整体连边角度构造,本文由社区内节点的连边角度,考虑节点的连边密度,将提出一种社区的平均密度评价指标。并通过密度传播和最优化平均密度,得到二分网络的社区发现算法。
2.1 社区的平均密度
对给定二分网络进行社区划分,使得社区内部连接相对较密集,社区间的连接相对较分散。若社区中的节点与其所在社区内的节点连边越多,则与其他社区节点的连边越少,即这个二分网络的社区结构越好。依据此思想本文定义了二分网络的平均密度,为给出此平均密度的定义,先定义社区内节点的连边密度。
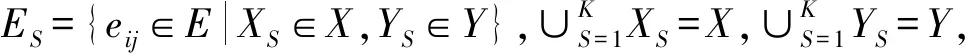
(1)
式中:
ki为X型节点xi的度;
j为Y型节点下标;
p为二分网络中Y型节点的总数;
yj为Y型节点中的节点;
aij为邻接矩阵A中的元素;

同理,对于第S个社区内Y型节点yj的连边密度定义为节点yj在S社区内的连边比例,具体定义为:
(2)
式中:q为二分网络中X型节点的总数;i为X型节点下标。
社区S中节点的平均连边密度定义为:
(3)
式中:|XS|表示社区S中X型节点个数;|YS|表示社区S中Y型节点个数。式(3)可简写为:
式中:i为社区中第i个节点;为与i节点相对的另一种类型节点。
二分网络社区的平均密度定义为K个社区的平均密度,具体定义为:
(4)
式中:K表示社区划分个数。
由式(4)可知,社区的平均密度越大,其社区内部节点连接越紧密,那么,社区划分效果也相对越好。因此,可以利用社区的平均密度刻画社区划分结果的好坏。当社区中的节点连边均与社区内部的节点连边时,社区的平均密度D达到最大值1,此时的划分社区结果最好;当社区内的节点的连边均与社区外的节点连边时,社区的平均密度D达到最小值0,此时的社区结构最差。
2.2 算法设计
利用社区的平均密度划分社区,可通过优化社区平均密度的方法进行社区发现。本文提出的连边密度传播算法(EDPR),首先,初始化其中一类节点的社区;然后,将节点密度大于参数θ的另一类节点加入到社区中;最后,通过节点连接密度D(xi)和D(yj)不断更新节点标签,使社区的平均密度D达到最大,即可获得二分网络的最终社区划分结果。具体算法如下:
输入:二分网络G(X,Y,E)的邻接矩阵A和参数θ。
输出:二分网络社区发现最终结果F1,F2,…,Fk。
Step1初始化X型节点社区,将X型节点中节点xi分别分配到一个社区中,令xi∈Gi,t=0,D=0;
Step2将Y型节点yj分配到与其有连边的Gi社区中;
Step3根据式(1)重新更新X型节点的社区,将节点xi分配到使得D(xi)>θ的社区中,并更新为Gi,且将X型节点从原先所属的社区中删去;
Step4由式(2)分别计算Y类型节点yj在社区Gi中的节点密度D(yj),并将节点yj分配到使得式(2)最大的Gi社区中;
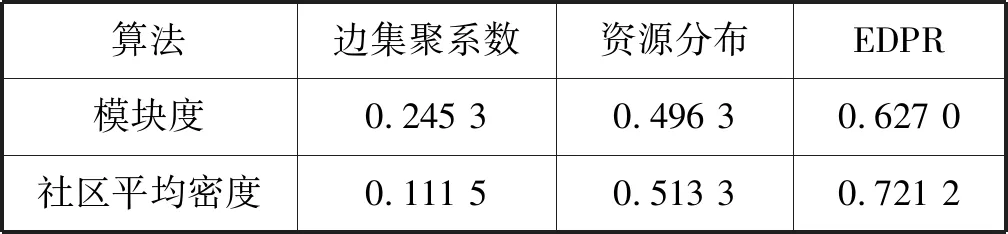
Step5根据式(4)计算社区的平均密度D,若D(t+1) Step6迭代更新,直到二分网络的平均密度D最大,即为社区划分的最终结果F1,F2,…,Fk。 算法的Step 3为了确保X型节点社区更新,从第二次迭代开始变为根据式(1)寻找使得D(xi)最大的社区Gi,并更新xi的标签。 虽然Barber和Murata的模块度得到了广泛应用,但是这两个模块度指标存在一些分辨率限制。本文提出的二分网络的平均密度D能够克服模块度在一个完全图上的分辨率限制,主要通过一个具体的实例说明。 如图1所示,二分网络是由一个完全图Kn,n组成,该完全图是由n个X型节点和n个Y型节点(n≥2)和n2条边组成。这个二分网络中共有2n个节点和n2条边。 (a) (b)图1 由完全图Kn,n组成的二分网络 考虑如下两个社区划分结果: P0:整个二分网络视为一个社区,如图1(a)所示。 P1:将二分网络划分为两个社区C1和C2,社区C1中X型节点和Y型节点均有n1个,社区C2中X型节点和Y型节点均有n2个,n1+n2=n。如图1(b)所示。 由图1可以很明显得出,划分P0要比P1好,然而,对于以上两个划分结果,用Barber和Murata的模块度计算求得的模块度值均为0[18]。因此利用Barber和Murata的模块度无法评价这两种划分的好坏。 本文提出的二分网络的平均密度D,对P0和P1两个划分评价的计算: 在人工网络和真实网络上验证EDPR算法的性能,同三种较经典的算法(BRIM算法、边集聚系数算法和资源分布算法)比较模块度和社区平均密度值。 为检验EDPR算法在给定网络结构下,社区划分的准确性,特在8个人工二分网络上进行测试。其中每个网络中节点的度均为k=64,k=kin+kout,kin表示节点与社区中节点连边个数,kout=0,1,…,7表示节点与其他社区节点的连边数。具体的网络信息如表1所示。 表1 构建的人工网络信息 分别在人工二分网络上,应用EDPR算法聚类,并与BRIM算法、边集聚系数算法和资源分布算法的聚类结果比较,互信息指标作为评价指标。如图2所示,EDPR算法总能准确自主地划分这8个人工二分网络的社区。由于EDPR算法始终寻找使得节点连边数最大的社区,所以在每次实验中,EDPR算法总能精确的将节点分配到与其连接最紧密的社区中,求得互信息指标为1,故划分准确性均为1。EDPR算法不仅准确性比其他三种算法都高,而且可以自主地确定社区划分个数。其中,边集聚系数算法在人工网络数据集上的划分准确性出现了较大的波动,且在kout=4时,正确率仅为0.533 8。资源分布算法和BRIM算法在kout=0,1,…,7的网络上虽无明显波动,但其正确率也不及EDPR算法。 图2 四种算法分类正确率比较 本节分别在3个真实数据:Moreno Crime(http://konect.uni-koblenz.de/networks/moreno_crime)、Southern Women Data[24]和Scotland Data[25]上验证EDPR算法的准确度。并与3种经典算法—BRIM、边集聚系数算法、资源分布算法比较模块度和社区平均密度值。 实验1: Southern Women Data是由Divas等收集的1930年的密西西比州,由18位妇女和14个活动组成的数据,被广泛地应用于对二分网络社区发现算法准确性的检测中。 社区分布图如图3所示,将数据集中的妇女用圆形表示,编号为1~18,活动用矩形表示编号为1~14,图中的连边表示妇女参加了相应的活动。Southern Women Data数据集上,EDPR算法将其划分为2个社区,其中,第一类为活动{1,2,3,4,5,6,7,8}与妇女{1,2,3,4,5,6,7,8,9},第二类为活动{9,10,11,12,13,14}与妇女{10,11,12,13,14,15,16,17,18}。计算得此划分模块度和社区平均密度值分别为0.333 2和0.870 1。图3中,不同的灰度表示不同的社区。 图3 在数据集Southern Women上的社区划分 在Southern Women数据集上,分别采用边集聚系数、BRIM和资源分布算法划分社区,并计算对应的模块度和社区平均密度值。进行多次实验,取平均值同EDPR比较,比较结果如表2所示。 由表2可知,在Southern Women数据集上,由EDPR算法求得的模块度和社区平均密度值,都比其他三种算法求得的值略高,表明所划分的社区结构更加明显,划分准确性也相对较高。 实验2: Moreno Crime数据集,是由551起刑事案件和与刑事案件有关的829名人员,1 476条连边构成。网络中一类节点表示案件中的一个受害者、目击者或嫌疑人,另一类节点是相应的案件。 在Moreno Crime数据集上,EDPR将其分为185个社区,例如人员{1,93,694,756}与案件{1,2,3,4}为一个社区;人员{77,205}与案件{98,127}分为一个社区;案件{108,109,180,279,593,709,814}与人员{163,164,165,166,167,168}为一个社区;相应的模块度和社区平均密度值分别为0.971 0和0.907 7。 分别采用边集聚系数、资源分布和BRIM 3种算法划分社区,同时计算3种算法对应的模块度和社区平均密度。比较结果如表3所示。 由表3可知,在Moreno Crime数据集上,EDPR算法的精确度高于三种经典算法,能够较好地识别社区。 实验3: Scotland Data是一个较典型的二分网络数据集,该数据集描述了苏格兰早期108家连锁企业和136位股东之间的任职情况。将该数据表示成一个二分网络,网络中的两类节点代表公司和股东,节点间连边表示该股东在公司任职。 在Scotland Data数据集上,EDPR将其分为25个社区,例如公司{11,28}与股东{2,48,59,60}为一个社区;公司{63,93,103,104}与股东{3,16,36,131}分为一个社区;公司{78,66,95}与股东{82,85,132,120,121}为一个社区;相应模块度和社区平均密度值分别为0.627 0和0.721 2。 分别采用边集聚系数、资源分布2种算法划分社区,同时计算2种算法对应的模块度和社区平均密度值。进行多次实验,取其最大的模块度值同EDPR比较。在Scotland Data数据集上模块度和社区平均密度值比较结果如表4所示。 表4 Scotland Data数据集上的比较 由表4可知,在Scotland Data数据集上,EDPR算法求得的模块度和社区平均密度值更大,表现更佳。说明EDPR算法可较好地挖掘社区结构,社区划分准确性相对更高。 本文从社区的节点出发,构造了节点的连边密度和社区的平均密度,同时验证了社区的平均密度作为评价指标,可克服模块度在特定网络上的分辨率限制。并提出了一种二分网络发现算法——连边密度传播算法(EDPR),通过实验验证该算法可较好地发现社区,划分准确度也较高。希望在今后可以对多模数据做进一步研究。2.3 分辨率限制的证明



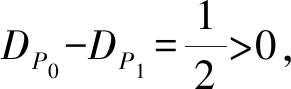
3 实验结果与分析
3.1 人工网络实验


3.2 真实网络上的实验

4 结 语
