马尔科夫与ARIMA组合模型对地区降雨量的预测研究

徐梦茹 王学明

1(宁夏大学信息工程学院 宁夏 银川 750001)2(宁夏大学网络信息管理中心 宁夏 银川 750001)

0 引 言

年降雨量与地区农作物收成、交通出行等方面息息相关。降雨量的多少将直接影响地区经济发展，尤其是农业方面的发展，降雨量太多或太少都会造成农作物的歉收；降雨量的多少也会影响流域水资源的丰富程度。若能够将年降雨量准确预测出来，这将对防洪抗洪、农业生产工作起到非常大的积极作用。但因为地理位置的差异，各个地方对于降雨量的预测需要因地而异。本文根据某地区从1949年到2017年的年降雨量历史数据对2018年的年降雨量数值作出预测，通过此次实验为准确预报年降雨量提供合理的依据。降雨量预测流程如图1所示。

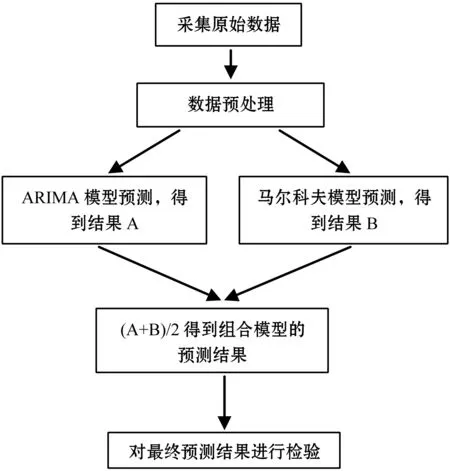
图1 降雨量预测流程

1 马尔科夫模型

一般要预测事物发展的趋势，必须要知道此事物历史情况与当前情况，并加以综合考虑，同时有相当一部分的预测方法需要知道预测事物的历史及当下数据，才能进行建模，并应用于实际生活中。但马尔科夫模型则认为只要知道当前的状态，便可以预测未来的情况，不需要知道事物发展的历史状态。这种性质称为马尔科夫性[1-2]。马尔科夫模型是根据系统状态之间的转移概率来预测系统的未来发展。

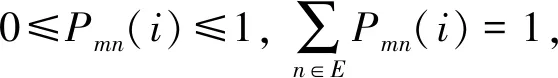
定义2将转移频数矩阵的第j列之和除以所有转移频数之和，所得值为边际概率，记为P·j，即有：

(1)

当n充分大时，统计量服从自由度为(m-1)2的X2分布。其公式如下：

(2)

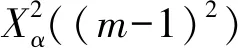
定义3数据序列是相依的随机变量，采用自相关系数作为相依关系强弱的度量，第s步的自相关系数为：

(3)

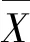
(4)

式中：ωs为第s步的马尔科夫权重;l为最大转移步数。

2 ARIMA模型

ARIMA模型的基本思想是将预测对象随时间推移而形成的数据序列视为一个随机序列，用一定的数学模型来近似描述这个序列。它的具体形式可以表达成ARIMA(p,d,q)，其中：p表示自回归过程的阶数；d表示查分阶数；q表示移动平均过程的阶数[3-4]。ARIMA模型建模过程及具体步骤如图2所示。

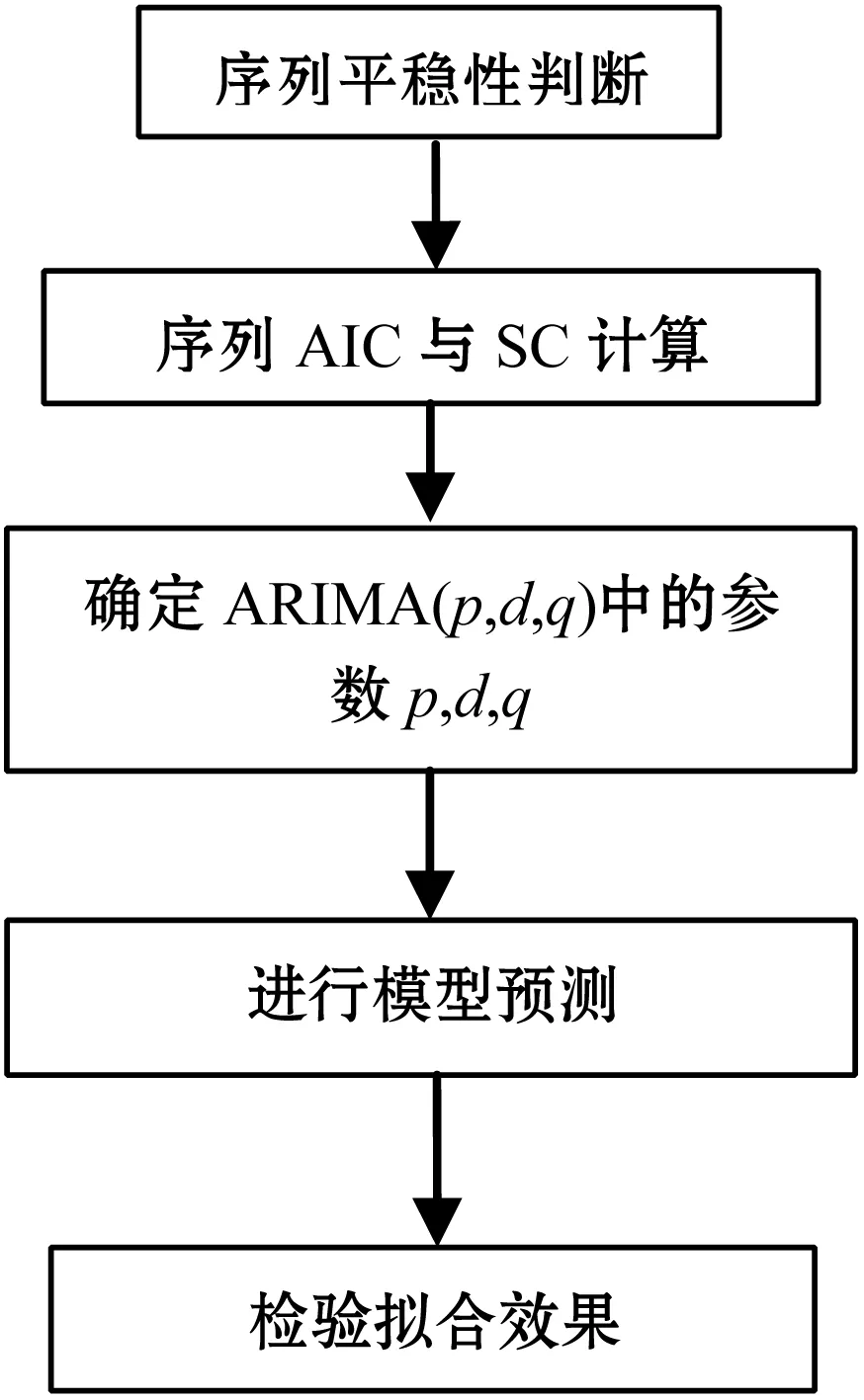
图2 ARIMA模型预测流程

3 实验过程及结果

实验选取的原始数据为某地区1949年-2017年的年降雨量数据。其中，将1949年-2014年数据作为模型训练集，2015年-2017年数据作为模型测试集，所有预测过程均用MATLAB与R语言完成。

3.1 ARIMA模型预测

(1) 序列平稳性判断。根据降雨量数据做出时序图，如图3所示。

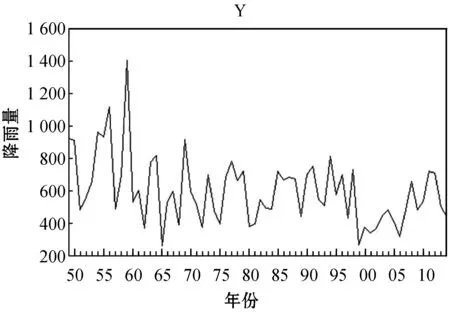
图3 序列时序图

根据时序图可知原数据接近平稳，之后用ADF单位根检验法来进行检验，通过计算得出Dickey-Fuller=-6.662 674，概率P=0.000 0<0.05，说明序列平稳，不用进行差分平稳化数据，故ARIMA(p,d,q)中d=0。

(2) 模型识别。根据数据得出自相关图与偏自相关图，如图4、图5所示。

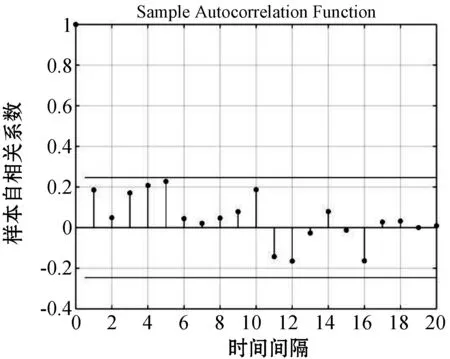
图4 自相关图

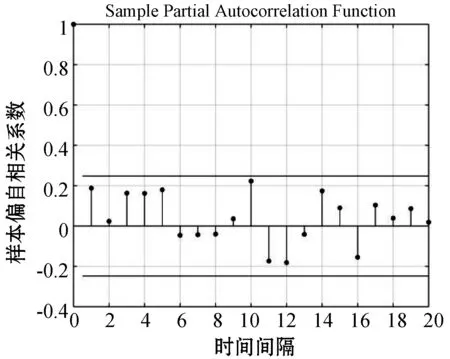
图5 偏自相关图

选取部分(p,q)来进行AIC验证，得到各模型检验结果，如表1所示。

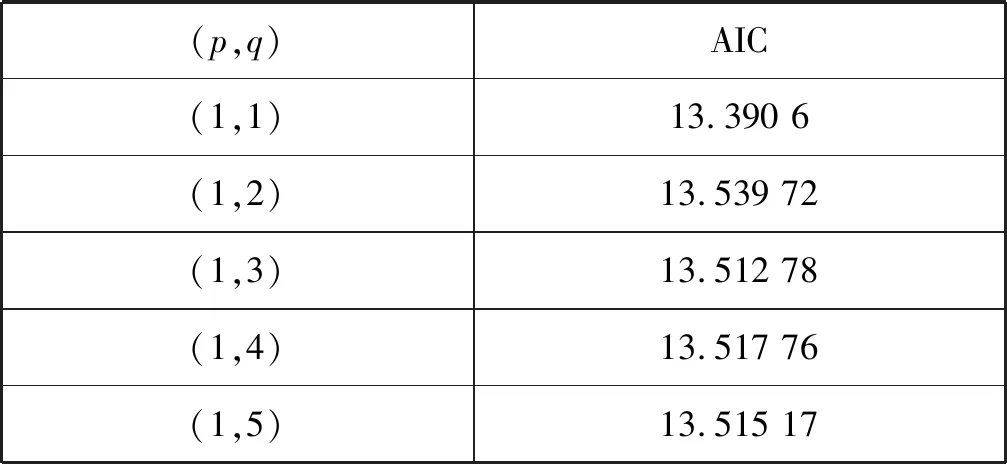
表1 模型检验结果

从表1中可知,当(p,q)=(1,1)时AIC 的值最小，理应选择p=1、q=1，但经过后期误差分析可知，当p=1、q=5时误差最小，即预测最准确，所以本实验中的ARIMA模型选用ARIMA(1,0,5)[5]。

(3) 模型预测。经过预测，得到2015年的降雨量预测值为565.894 8 mm，2016年的降雨量预测值为614.572 6 mm，2017年降雨量预测值为611.973 6 mm，平均相对误差为3.94%，预测结果较好。并将其应用于2018年降雨量预测，得到预测值为579.165 1 mm。

3.2 马尔科夫模型预测

(1) 马氏性检验。根据规定，一般情况下，当年降雨量t小于平均降雨量的-25%为枯水年，小于-10%偏枯年，-10%～10%为平水年，大于10%为偏丰年，大于25%为丰水年[6]。由此可以将降雨量划分为5个等级，如表2所示。

表2 降雨量等级状态划分

由此得到：

各步转移概率为：

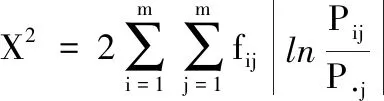
表3 统计量计算表

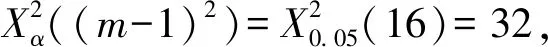
(2) 预测过程:

① 计算各阶自相关系数及权重。由式(3)求得序列各阶自相关系数r=(0.186,0.049,0.171,0.208,0.228)，再由式(4)得权重向量为ω=(0.206 2,0.054 3,0.189 6,0.230 6,0.252 8)。

② 根据1949年-2014年的历史降雨量数据分别预测2015年-2017年降雨量数据。以2015年为例，如表4所示。

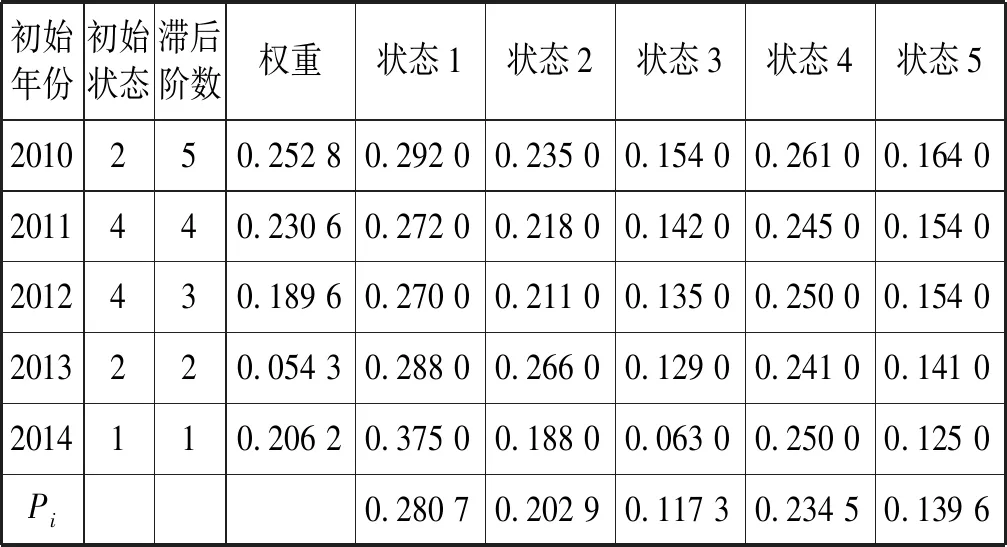
表4 2015年降水量预测状态

由表4可知，将同一概率加权后的最大值为0.290 7，即2015年的预测状态为1，同理可得2016年、2017年预测状态分别为3和3，同时求得2015年到2017年的预测降雨量分别为499.33 mm、599.1 mm、599.1 mm。实际上2015年到2017年的降水状态都为3，得出平均相对误差为10.17%。

最后根据实际2013年到2017年降水量数据，得到2018年预测的状态为2，降水量预测为519.26 mm。

3.3 两种模型组合预测

通常，ARIMA模型较为简单，只需要内生变量而不需要借助其他外生变量，但是其本质上只能用来预测线性关系，不能预测非线性关系[7]。马尔可夫模型不适合用于系统中长期数据的预测，理论上只能用于预测短期内的数据[8]。基于对以上两种模型的分析，本文将ARIMA模型得到的预测结果与马尔科夫模型的预测结果进行求平均值的操作，见表5。

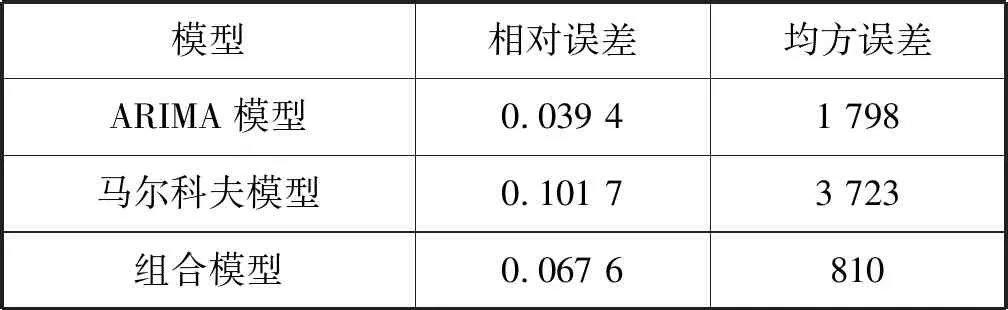
表5 预测模型误差对比

在相对误差相差不大的情况下，组合模型的均方误差相较ARIMA模型和马尔科夫模型的均方误差明显下降，说明组合模型预测的稳定性较高，此组合模型有较高的应用价值。

4 结 语

本文通过将两种模型组合对地区降雨量进行预测，所达到的预测结果较好。基于目前降雨量预测模型，本文所提出的组合模型还有一些地方需要进一步改进，以提高预测准确度和稳定性。预测准确度的提高将有利于相关部门制定相关的方案措施来应对不同的降雨量带来的后果，做到防患于未然。