基于单桩载荷试验的铁路路基桩筏基础沉降计算

2019-03-31陈洪运宋绪国郭帅杰

铁道勘察 2019年6期

陈洪运宋绪国郭帅杰

(1. 中国铁路设计集团有限公司，天津 300251; 2. 中国铁路设计集团有限公司轨道交通勘察设计工程实验室，天津 300251)

《高速铁路设计规范》对路基工后沉降的控制十分严格[1]。为有效控制路基沉降，常采用刚性群桩基础进行地基加固处理。路基沉降主要由底部的桩基沉降造成。因此，可采用设计阶段的理论计算[2]与施工阶段(基于沉降监测数据)的预测评估[3]相结合的方法预估桩基沉降，以提高高速铁路路基工后沉降预估的准确性。群桩沉降计算常采用复合模量法和实体基础法，将包含桩体与土体的加固区当作均质体，没有考虑桩-桩相互作用、桩筏基础与桩网基础的桩顶约束等因素对沉降的影响，其计算结果为路基的平均沉降。实际工程中，常规路基的横断面还存在内大外小的凹形沉降。通过实际沉降监测数据预测工后沉降的方法，需要大量的仪器设备和长期的监测数据，才能得到较为合理的沉降预测值，总体而言成本较高，而且还可能会出现监测数据跳动大等问题。

另外，当采用群桩基础进行铁路路基的地基加固时，施工过程中必须对不少于群桩总数1%的单桩进行静载试验[4-5]，其单桩静载p-s 曲线中包含着丰富的桩土相互作用信息，若仅进行单桩承载力的判定，其功能就略显单一。

综上所述，现有的路基工后沉降预估方法存在理论模型考虑不周全和监测数据获取成本高、数据不稳定等问题，而属于原位试验的单桩静载试验可以真实地反映现场不同荷载作用下的桩土相互作用。

提出一种铁路路基桩筏基础简化模型，基于单桩p-s 曲线和桩、土的相互作用系数[6-7]，给出了一种铁路路基桩筏基础的沉降预测方法，可以计算出不同位置处桩、土、筏的不均匀沉降。

1 桩筏基础模型

1.1 基本假定

桩筏基础筏板受力与变形的求解是一个空间问题，如果通过弹性力学方法对其进行精确求解，过程会十分复杂[8]，为简化计算，将筏板划分为垂直于线路方向的板带，板带的分界线为相邻桩间的中线(见图1)，忽略板带间剪力影响，用位于板带轴线的多跨连续梁结构表示板带并进行内力计算[9]。

图1 筏基板带

在桩筏基础沉降分析模型中(见图2)，将筏板简化成连续梁，其上作用有分布力;将桩体简化成简支支座，竖向位移为0;将梁下土体假定为Winkler 弹性地基模型。

图2 多跨连续简支弹性地基梁

该方法的基本分析思路如下:

①将桩筏基础简化为图2 所示的多跨连续简支弹性地基梁，按照弹性地基梁的相关理论，根据已知边界条件，解得各支点处的变形与内力。

②根据解得的各支点处左右两侧的剪力，可以得到支点反力，即桩顶反力。

③根据解得的各支点处变形与内力，即可求得各跨任意位置处的变形y(x)，将变形y(x)沿跨长积分，乘以地基系数，可求得各跨梁下土体承担的荷载。

④从单桩p-s 曲线中获得单桩刚度，结合桩、土相互作用的影响，求得群桩中的单桩刚度。

⑤通过地质资料获得Winkler 弹性地基的基床系数，结合桩、土相互作用的影响，求得群桩中的土单元刚度。

⑥桩土荷载除以群桩中的桩土刚度，得出桩土位移。

1.2 多跨连续梁模型

Winkler 弹性地基梁任一截面处的位移y(x)、转角θ(x)、弯矩M(x)、剪力Q(x)如图3 所示。

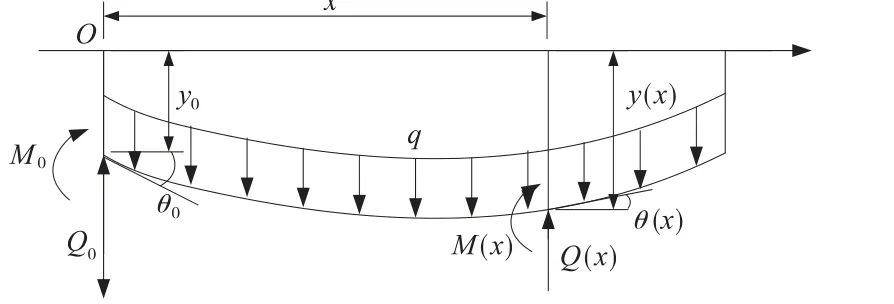
图3 弹性地基梁变形和内力示意

多跨连续简支弹性地基梁模型各支座的位移yi=0，两端支座的弯矩M0=Mn=0，中间各支座左右两端的弯矩相等，Mi(l)= Mi+1(0)、转角相等，θi(l)= θi+1(0)。根据上述已知条件，以2 跨为例，可以得出各支点处的变形和内力计算矩阵

通过式(3)，可求得各支点处变形和内力的解，依据上述流程，也可求得任意跨连续简支弹性地基梁各支点处的变形和内力，其中包括各支点剪力，通过简单换算后即可求得支点反力，即桩顶荷载。求得各支点处的变形和内力后，即可根据式(1)求得各跨任意位置处的变形和内力，对各跨位移y(x)沿跨长积分后，乘以地基系数k，即可得到各跨底土体承受的荷载。同理，可对任意跨进行求解。

从单桩p-s 曲线中获得单桩刚度，结合桩、土相互作用的影响，获得群桩中的单桩刚度;通过载荷板试验获得土单元刚度，结合桩、土相互作用的影响，获得群桩中的土单元刚度。将上述求得的桩土荷载除以群桩中的桩土刚度，即可获得桩土位移。

1.3 桩土刚度

单桩静载荷试验确定了单桩桩顶荷载p 与桩顶竖向位移s 之间的关系，体现了不同大小的荷载作用下桩体与桩周各层土体之间的相互作用。因此，可以通过单桩p-s 曲线获得单桩刚度，结合桩、土相互作用的影响，进而可以求得群桩基础中单桩的刚度[11-12]。

桩体刚度的定义为:在桩顶位移s 很小时，使桩顶发生单位竖向位移ds 时的竖向荷载dp，即K=dp/ds。但是，由单桩p-s 曲线获得的单桩刚度还不是群桩基础中某根桩的刚度，群桩基础中某根桩的刚度不仅与单桩刚度有关系，还受到群桩中某根桩的位置和荷载影响，其刚度需要联合单桩p-s 曲线与群桩基础中的桩、土相互作用系数来求得。为研究群桩基础中桩与桩之间的相互影响，桩-桩相互作用系数的概念被提出。在常规的桩-桩相互作用系数求解方法中，由于没有考虑桩体的存在，导致所求得的桩-桩相互作用系数偏大。 Muki 提出了虚拟桩法，考虑了桩体的影响，将桩基分解为弹性半空间扩展土和虚拟桩的叠加，基于桩土界面的位移协调条件，构建了第二类Fredholm 积分方程[6-7]

式中:Ef=Ep-Es为虚拟桩模量，Ep为桩体模量，Es为土体模量，vs为土体泊松比，pf(z)为虚拟桩中z处的轴力，A 为桩体横截面面积，(z，ζ)表示作用在截面Πξ，j的单位荷载引起截面Πz，i的平均应变。

根据桩体位移与虚拟土的位移存在变形协调的关系，结合式(4)解得的虚拟桩轴力pf(z)，可以得到桩身不同位置处的位移

桩-桩相互作用系数αij是桩j 引起桩i 的附加沉降与桩i 因自身荷载引起沉降的比值，基于式(5)，有

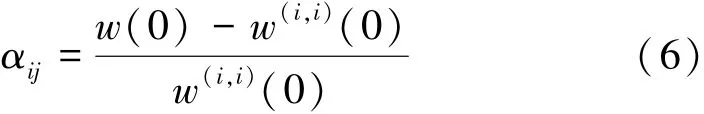
式中:w(i，i)(0)是单位竖向荷载下单桩的桩顶位移，可以从式(4)、式(5)中除去与桩j 相关的参数来获得。

同理，也可获得桩-土、土-桩、土-土相互作用系数。求解过程中，为方便处理，将桩间土划分为一个个单元格，并将单元格等效为圆形。

群桩基础中某根桩的刚度实际上是在该桩顶部发生一个单位位移时，群桩基础中所有桩单元与土单元所承受的荷载。结合通过单桩p-s 曲线获得的单桩刚度与基于弹性理论解的桩、土相互作用系数，群桩基础中桩i 的刚度为

式中:1/δpi为通过单桩p-s 曲线获得的单桩刚度;αij为桩j 对桩i 的相互作用系数;φik为土单元k 对桩i 的相互作用系数;ppi、ppj、psk分别为作用在桩i、桩j、土单元k 上的荷载。

同理，可获得群桩基础中某处土单元的刚度。

虽然路基底面宽度有限，但沿线路方向的长度较大，往往远超出桩、土单元相互作用的影响范围。因此，对于铁路路基，需要确定其相互作用系数的叠加范围。

郭帅杰[13]以前后两排桩基之间附加应力差值小于10%为控制标准，研究了铁路路基中路堤填土高度H、桩间距s、桩体直径d、桩体长度L、下卧层厚度Lx等因素对加固区和下卧层附加应力荷载的叠加范围，确定了不同工况中铁路路基条形荷载作用下的桩体荷载叠加范围，并对相关影响因素与叠加范围的关系进行了拟合

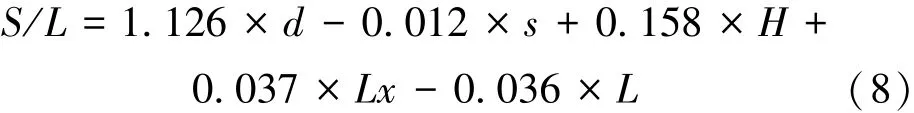
式中:S 为荷载影响范围。

综上，桩的刚度直接取之于单桩p-s 曲线，土的刚度可以从载荷板试验或基床系数获得，并考虑群桩基础中各桩单元、土单元之间相互作用的影响及影响范围，最后解得群桩基础中的桩、土刚度。

1.4 位移计算

桩、土荷载分别对应地除以群桩中的桩、土刚度，即可得出桩、土位移。

采用纯弹性模型计算其相互作用系数，可能会导致计算得出的沉降位移比实测值偏大[14]。因此，可将相互作用系数乘以修正系数来解决这个问题。

2 工程实例

2.1 工程实例一

为满足工后沉降要求，京津城际武清段采用了桩筏基础，以减小软土段的路基沉降。路基断面结构形式如图4 所示，两侧为扶壁挡土墙，基础底面为钢筋混凝土筏板，筏板厚度为0.5 m，混凝土等级为C30;筏板底面的碎石垫层厚度为0.15 m;采用CFG 桩进行地基加固，布桩形式为正方形，每个断面15 根桩，桩间距约为1.5 m，桩体长度为27.65 m，桩体直径为0.4 m;施工过程中进行了单桩静载试验(见图5)与地基沉降的长期监测(见图6)[15]。

图4 CFG 桩断面

图5 单桩静载试验的荷载-位移曲线

图6 断面沉降-时间-填土关系曲线

从图5 可以看出，加载到500 kN(设计荷载)时的沉降量为1.81 mm;加载至1 000 kN 时，曲线基本呈线性关系;当加载到1 125 kN 时，桩顶的总沉降为8.9 mm;当加载至1 250 kN 时，桩顶沉降突然增大，混凝土试桩已经破坏。

由图6 可以看出，前310 d，荷载增量较小，相对应的路基断面沉降也较小;随后开始预压堆载，荷载增加至200 kPa;480 d 后卸载，荷载降低至约160 kPa。沉降监测截止时，线路中心沉降为66.5 mm，线路坡脚沉降为54.3 mm，路基断面中间的沉降较坡脚大12 mm左右。

采用基于单桩静载试验计算群桩沉降的方法，设桩体弹性模量为20 GPa，土体弹性模量为25 MPa，土体泊松比为0.3;用于计算相互作用系数;设筏板弹性模量为30 GPa，地基土体基床系数20 为MN/m3，用于考虑筏板效应的桩-土-筏协同作用[16-17]。通过式(8)，确定群桩叠加范围为42.8 m。该实例的地基横断面沉降位移计算结果如图7 所示。

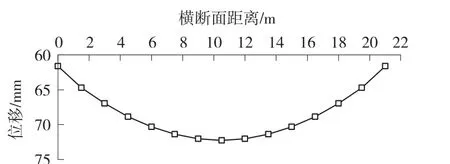
图7 横断面沉降的理论解

如图7 所示，地基横断面位移呈现出中间大、边侧小的凹形规律，路基断面中间的沉降约比坡脚沉降大11 mm，与实测结果吻合较好。总体沉降量的理论值约比实测值大6 mm(偏安全)。从图6 可以看出，监测结束时，沉降尚未完全稳定。

2.2 工程实例二

德国马克斯·博格公司对京津城际路基段进行了沉降量检算。

路基段土层为正常黏性固结土，最大勘探深度处的土层为黏土与粉土，局部含有机混合物。黏土为硬塑，局部软塑，在较深处为硬塑-坚硬。不同深度处有砂层，砂层含不同体量的泥土。地下水离地表较近，在地表以下0.5～3.1 m 处。土层参数见表1。

表1 土层参数

打入桩桩径为0.45 m，桩长21.5 m，桩间距1.7 m，一排共6 根桩。筏板宽9.3 m，厚0.5 m。每排桩承担的总荷载为896 kN，包括活载、轨道板、垫层、筏板等。

对打入桩进行了静载试验，在试验桩轴线中心采用千斤顶压力控制加载，与压重相连的反力梁作为千斤顶的承台，荷载由在试桩与千斤顶之间的压力表来控制，试桩端头的沉降由电子位移传感器测量。工点处的单桩静载试验的荷载-位移曲线见图8。

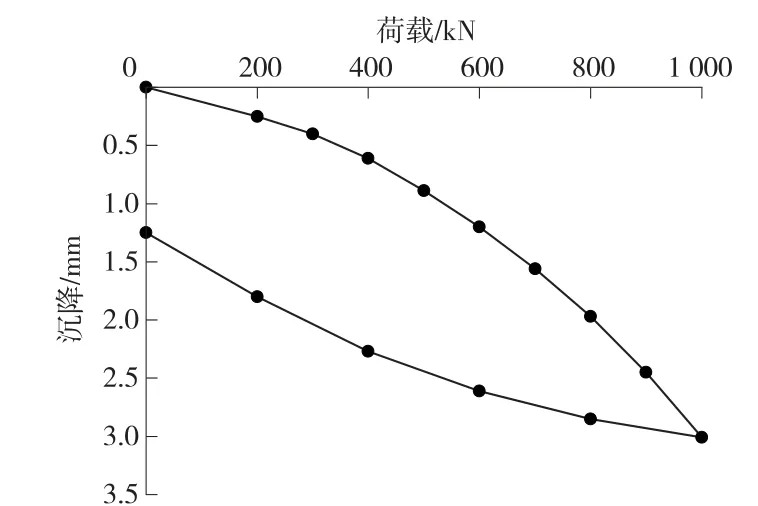
图8 单桩静载试验的荷载-位移曲线

如图8 所示，加载至1 000 kN 时桩顶位移仅3 mm，桩体仍未破坏。随后，完成了桩体的卸荷测试。

在采用基于单桩静载试验计算群桩沉降的方法中，设桩体弹性模量为20 GPa，土体弹性模量为20 MPa，土体泊松比为0.3，用于计算相互作用系数;设筏板弹性模量为30 GPa，地基土体基床系数为20 MN/m3，用于考虑筏板效应的桩-土-筏协同作用;通过式(8)确定群桩叠加范围为13.5 m，由于不同桩位处桩体的叠加范围不同，最终导致不同位置处桩体的沉降差异。相关计算结果见图9。