空间圆拟合在钢安全壳闸门套筒安装测量中的应用
2019-03-31范祖贵
范祖贵
(中机国能电力工程有限公司,上海 200061)
1 概述
核电厂钢安全壳结构是压水堆核电厂反应堆的内层屏蔽结构[1],由中间柱形筒体及上下两个椭圆形封头组成,其中包括2 个设备闸门、2 个人员闸门及其它数以百计的贯穿件等(见图1)。 这些大型闸门套筒、贯穿件等均为圆环柱体结构(与钢安全壳焊接在一起),在拼装阶段,与安全壳同步完成[2]。
在安装测量时,对于直径较小的部件(如贯穿件),可先制作圆心靶座,然后直接测定内外侧圆心;对于直径较大的部件,无法直接制作圆心靶座[3],可采用全站仪在圆环端面上设站,通过测量套筒端面上平分的4 个点来间接获取圆心位置(其两两连线的交点被认定为圆心)。 由于测量及拟合方法的误差,使得该方法的安装精度较差。 而通过端面上的测量点,采用最小二乘方法拟合套筒端面圆心的方法,在核电行业中的应用案例极少。

图1 人员/设备闸门平面布置
关于空间圆拟合的方法很多,如文献[4]直接把空间圆看成平面圆进行拟合,但这种三维转二维的拟合方法存在一个明显缺陷,即无法保证所有的测量点完全在一个平面上,故其拟合精度不高。 文献[5,6]则是利用坐标投影、坐标转换等方式,对拟合平面上的测量点进行拟合,然后经过坐标反算,得到空间圆的圆心。 这种方法是目前使用最多也是较为成熟的一种方法,但其拟合过程复杂,实现起来也较为繁琐。 文献[7-13]则是分别拟合空间平面和球壳。 球壳的拟合采用球体的标准二次方程形式,用空间平面和球壳相交的方法确定空间圆,其方法大同小异,区别在于约束条件。 这种方法的数学模型更为严密,拟合计算过程也相对简单。
以下采用与文献[7-13]类似的方法,且以拟合空间平面作为约束条件,最终解算出空间圆的参数以及闸门套筒安装的其它参数,并判断其安装精度是否满足工程需求。
2 技术方案
钢安全壳人员/设备闸门现场安装的设计要求:(1)闸门中心线与水平/垂直方向的夹角误差不超过0.5°;(2)闸门实际位置(x,y,h)与设计位置(x,y,h)的误差不超过±25 mm。 为满足上述要求,可根据空间球体的性质,将套筒端面看成是一个球壳与过球心的空间平面形成的大圆,其球心即为套筒端面的圆心(见图2)。 拟合出空间平面后,运用中垂面理论和空间向量,推导出误差函数式(以空间平面为约束条件),利用最小二乘原理直接解算套筒内外侧端面圆心的坐标,同时计算出半径、平整度及圆度等参数,再通过两圆心的连线计算其与水平面(即过理论中心线的水平面)和垂直面(即与水平面垂直的竖向平面)的夹角,为现场安装指导以及安装后的检测提供依据。

图2 空间圆拟合示意
3 数学模型
3.1 数据采集
基于钢安全壳组装场地基准网[2],利用免棱镜全站仪分别测量布置于闸门套筒端面12 个测量点的三维坐标Pi(xi,yi,hi),如图3 所示。

图3 测量点布置示意
3.2 拟合方法
(1) 空间平面拟合
根据实测的闸门套筒端面点位三维坐标Pi(xi,yi,hi)(i=1,2,3,…,12),建立端面所在平面的平面方程axI+byi+chi-D=0,由于套筒端面圆平面不经过原点,为方便起见,直接认定D=1,同时将测量点的坐标值Pi(xi,yi,hi)代入,有

根据最小二乘原理VTPV=min,由于12 个测量点均为等精度观测,权阵取单位权阵,可得到平面方程的最小二乘解,也即是空间平面法向量的方向系数,表示为

(2)空间圆拟合
根据球体的中垂面性质,球心一定在球体上任意两点连线的中垂面上,而多个中垂面的交点一定是球心[3]。 设空间圆的圆心P0(x0,y0,h0),测量点Pj、Pk(j和k=1,2,3,…,12,j≠k),根据空间几何理论,向量

12 个测量点可以列出66 个中垂面等式,但是只有11 个中垂面等式是相互独立的,所以取k=i,j=j+1(i=1,2,…,11)。 同时认定第一步空间平面拟合的误差对空间圆拟合没有影响,并作为一个约束条件与11 个独立的中垂面等式联立,获得间接平差函数式

式中,
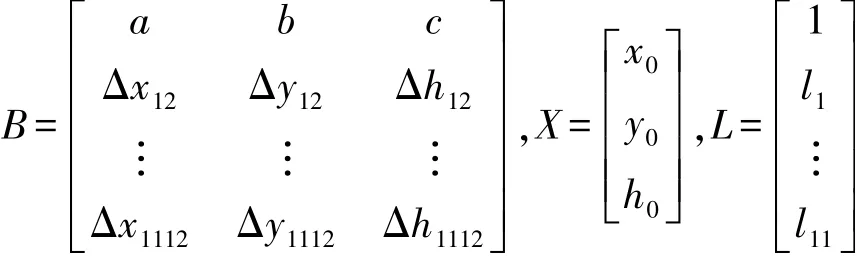
根据最小二乘原理,可得空间圆圆心的最优解为

由于加入了约束条件,权阵的选取应考虑权的差异性。 按照文献[8]的方法,令每一个中垂面方程的权为1,由于不在一条直线上的3 个点构成一个平面,该平面是由个平面拟合而成的最优平面,故拟合空间平面的权可取
(3) 精度评价
平面拟合的残差[4]
可理解为平整度,用实测点到拟合平面的距离来表示,计算式为

拟合圆的残差[4]可理解为圆度,用实测点到圆心距离ri与拟合半径r 的差值来表示,计算式为

其中ri= (xi- x0)2+ (yi- y0)2+ (hi- h0)2,
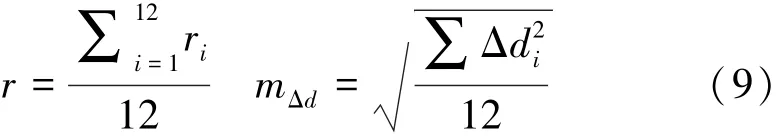
当某测量点的残差大于限差(限差一般可设定为2mΔd或3mΔd)时,则认为该点的观测值存在粗差。 应剔除粗差后重新解算参数,或重新测量该点的数据,从而获取最佳的拟合平面与拟合圆。
4 工程实例
以其中一个设备闸门套筒的安装测量数据为例,其内外侧测量点的观测数据如表1、表2 所示。
4.1 套筒内外侧圆心和平整度、圆度
根据表1、表2 的测量数据,利用式(2)、式(5),可分别计算门套管内外侧圆心(P、Q)的坐标和PQ 连线中心点O 的坐标,并计算其与设计坐标的差值(如表3 所示)。
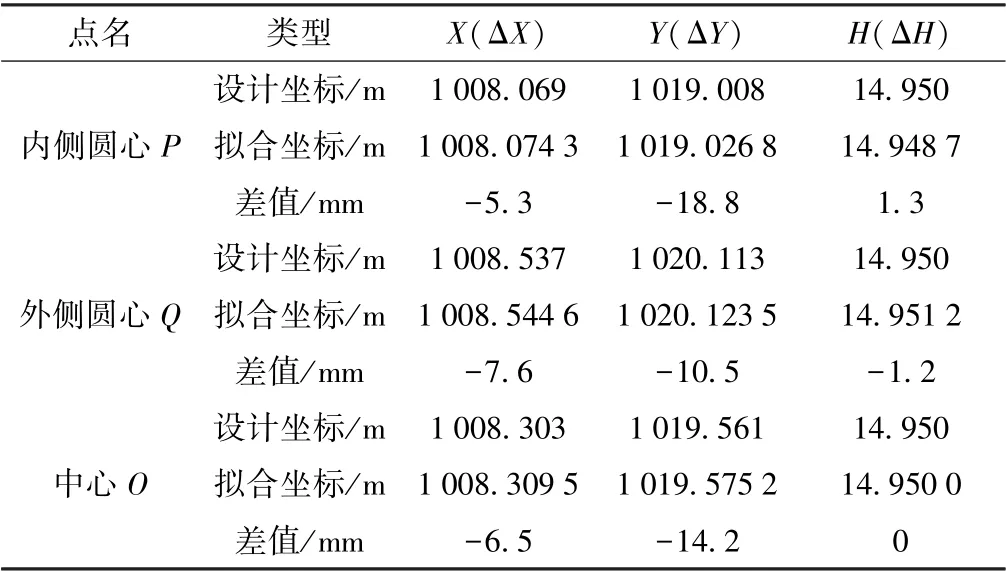
表3 圆心拟合坐标及差值
根据式(6)、式(8)可分别计算各个测量点的平整度和圆度,如表4、表5 所示。

表4 各个测量点的平整度与圆度(内侧) mm
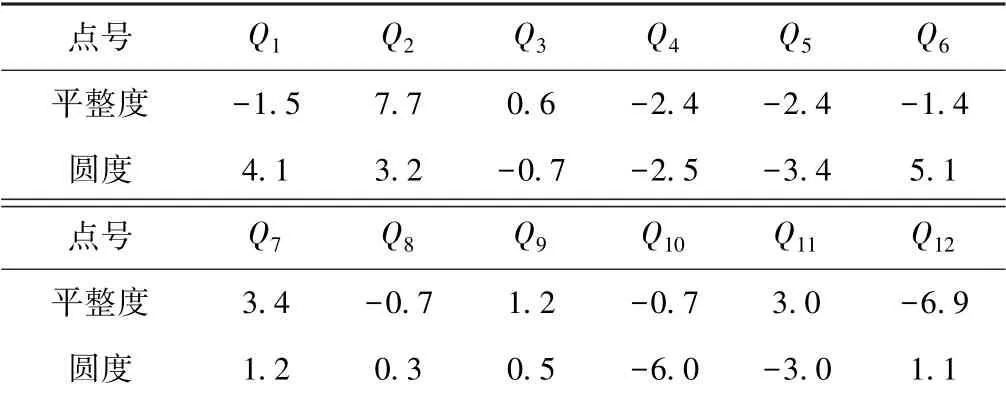
表5 各个测量点的平整度与圆度(外侧) mm
根据式(7)、式(9),分别计算内外侧测量点的残差中误差:md内= 3.8 mm,md外= 3.5 mm;mΔd内= 3.3 mm,mΔd外=3.1 mm。 表4 和表5 中,P12的平整度值最大,为8.2 mm,超过了2 倍残差中误差,但未超过3 倍的限差;而其余各测量点的平整度和圆度均未超过2 倍的限差。
4.2 与垂直面和水平面的夹角
理论上,闸门套筒内外侧端面圆心应处于同一水平面上,且圆心的连线PQ 应通过钢制安全壳的中心。 由于结构本身的制造误差、变形及安装误差,连线PQ 与垂直面和水平面存在一定的夹角,该夹角可利用三角函数理论公式直接计算。 本实例中,其水平面之间的夹角为16′22.23″,垂直平面的夹角为5′13.71″。
5 结束语
针对空间圆环柱体结构的安装与检测,提出一种新的数据处理方法。 该处理方法思路清晰,计算简单方便,可进行编程计算,亦可直接采用EXCEL公式进行计算。 配合高精度全站仪免棱镜测量功能,直接采集闸门套筒上测量点的三维坐标,可实现现场同步安装与检测,具有高效、快捷、精度高等特点。 数据采集时,测量点位应均匀分布,以避免病态矩阵的产生。
