模糊神经网络在阀门开度控制中的应用
2019-03-28朱天宇董全林
朱天宇,董全林,刘 日
(1.北京航空航天大学仪器科学与光电工程学院,北京 100191;2.微纳测控与低维物理教育部重点实验室,北京 100191)
0 引言
电磁阀控气缸系统作为智能阀门定位器的被控对象具有较强的非线性以及时变性,无法精确建立数学模型,而且智能阀门定位器还需要具备适应不同阀门的能力,常规PID控制方法无法根据被控对象的变化对参数进行调整。模糊控制和神经网络控制作为常见的两种智能控制方法对非线性问题都有不错的控制效果,将二者结合起来组成模糊神经网络则可以达到更好的控制效果。本文将模糊神经网络控制和PID控制相结合,利用模糊神经网络规则对PID参数在线整定,可以解决常规PID的问题,改善控制效果[1]。
在仿真分析中,利用AMESim建立被控对象模型,并联合MATLAB/Simulink进行联合仿真,实现控制器对系统控制效果的仿真分析[2];同时搭建了智能阀门定位器作为试验平台进行实验。
1 阀位控制系统组成及工作原理
智能阀门定位器闭环系统方框图如图1所示,它由微处理器、电气转换单元、气缸执行机构、阀门以及反馈位移传感器等部件组成。其工作原理是:阀门位置控制的指令信号和实际位置的反馈信号经控制系统运算处理及综合放大后,输出脉宽调制信号驱动开关电磁阀的启动和停止动作,完成向气缸腔体内的充放气,通过气缸活塞的运动使与活塞杆连接的阀门发生位置变换,控制其达到指令信号要求的位置[3]。

图1 系统总体方案设计
2 模糊神经网络PID控制器设计
2.1 控制器结构
模糊神经网络PID控制器结构如图2所示:控制器为二输入,分别为阀门位置的期望输出和实际输出。模糊神经网络经过训练以后对PID控制器的参数在线整定,并以PID参数KP、KI、KD为输出[4],PID控制器的输入为偏差,输出为控制量来控制阀杆的移动[5]。
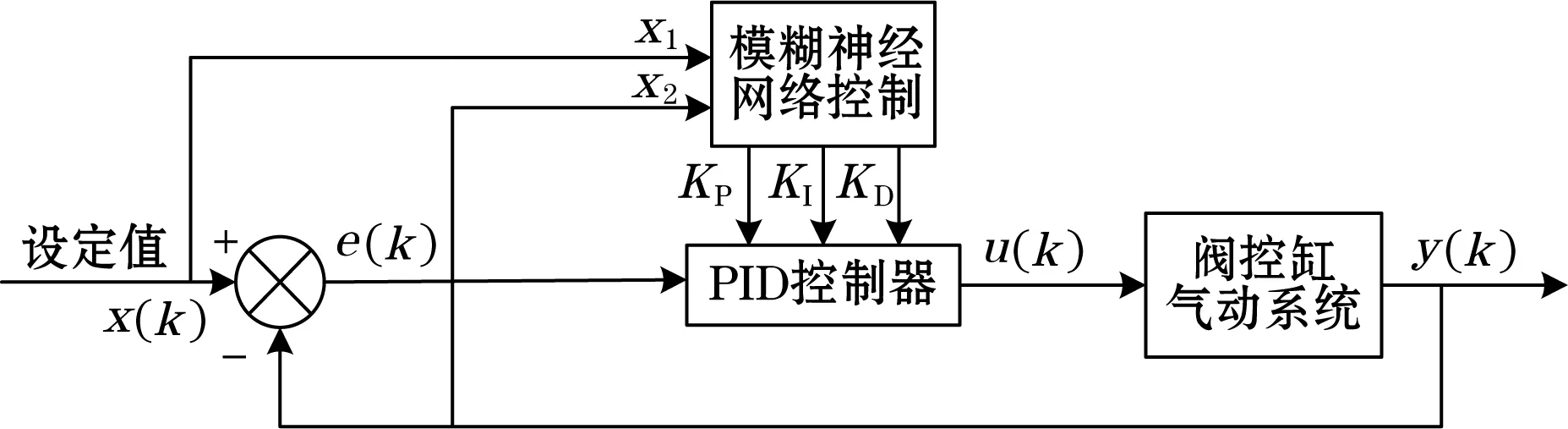
图2 模糊神经网络PID控制器结构图
模糊神经网络模型为如图3所示,由5层组成,除输入层和输出层之外共有三层隐层,分别负责模糊化、模糊推理以及归一化。输入层与模糊化层、模糊化层与模糊推理层、模糊推理层与归一化层之间的连接权均为1,只有归一化层与输出层之间的连接权需要调整[6]。
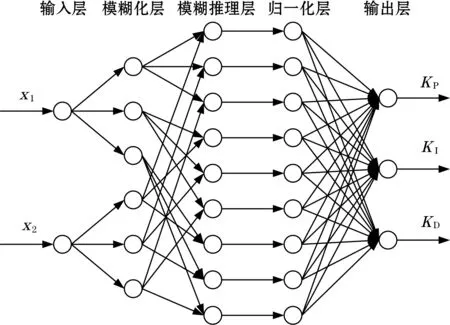
图3 模糊神经网络结构
对模糊神经网络中的每一层的具体功能做以下表示:
第一层:输入层
输入层的作用是负责连接输入值并将其传到模糊化层,每个分量可以表示一个语言变量。它起到将输入值传递到下一层的作用,该层节点总数N1=n。
第二层:模糊化层

(1)
式中:i=1,2,…,n;j=1,2,…,mi。
第三层:模糊推理层
本层的作用是匹配模糊规则,进行模糊推理,计算出每条规则的适用度。该层的节点j将其输入相乘后进行输出:
(2)
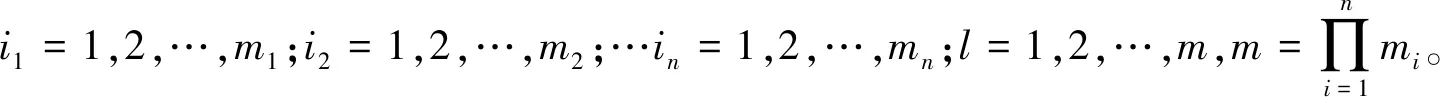
本层节点个数N3=m。
通常情况下,隶属度较大的点只存在于输入值附近,而其他节点的隶属度值则很小,近似为零。因此第三层的节点中只有少数节点不为零,多数节点输出都为零。
第四层:归一化层
该层节点个数与第三层结点个数相同,即N4=m,实现归一化,即:
(3)
式中:l=1,2,…,m。
第五层:输出层
输出层实现解模糊化运算,该层有3个节点,输出yk为KP,KI,KD的整定结果,即:
(4)
式中:wkl组成第四层各节点与输出节点的连接权矩阵,相当于yk的第j个语言值隶属度函数的中心值;k=1,2,3。
2.2 学习算法
该模糊神经网络PID算法需要学习的参数有模糊化层的隶属度函数的均值cij和标准差σij以及输出层的连接权wkl。
第一层:
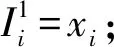
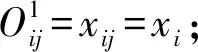
其中,i=1,2,…,n;j=1,2,…,mi。
第二层:


第三层:
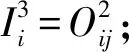
诱导局部域:


第四层:
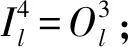
诱导局部域与输出:
第五层:

诱导局部域与输出:
式中:k=1,2,…,r。
PID控制器为
Δu(n)=KPxc(1)+KIxc(2)+KDxc(3)
(5)
式中:
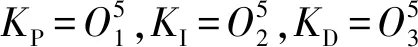
(6)
采用增量式PID算法
Δu(n)=u(n)-u(n-1)
(7)
采用Delta学习规则修正可调整参数,定义目标代价函数为
(8)
式中:rin(n)和yout(n)分别为整个控制系统的期望输出和实际输出。
模糊神经网络的权值和参数的学习算法推导如下:
首先计算第五层的局域梯度:
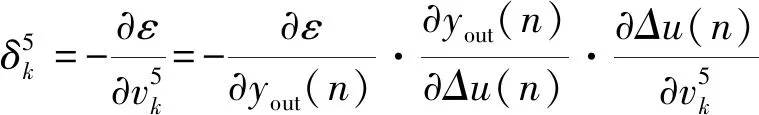
(9)
则可以得到:
(10)
进一步计算:
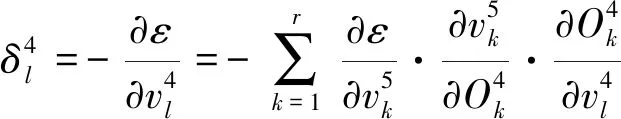
(11)

(12)
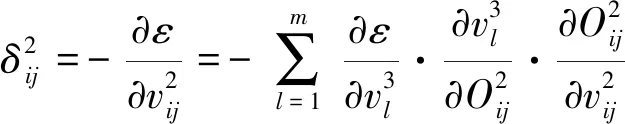
(13)
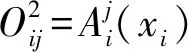
(14)
否则
(15)
从而可以求得一阶梯度为
(16)
(17)
在求得一阶梯度后,最后可以得到参数调整的学习算法。
(18)
(19)
(20)
式中:k=1,2,…,r;l=1,2,…,m;j=1,2,…,mi;η1、η2、η3为学习率;n为网络迭代步骤。
若考虑动量因子,则输出层的权值为
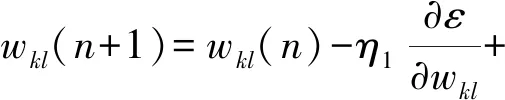
(21)
式中:n为网络的迭代步骤;α为学习动量因子。
对于该控制系统,输入量的两个分量分别为期望输出和实际输出,n=2。每个输入变量被模糊分割为7个语言变量值,则有m1=m2=7。由此得到第二层节点数为14;第三层和第四层节点数均为49,即可建立49条模糊规则;第五层有3个输出,分别为PID的3个参数KP、KI、KD,与每个节点相连接的网络权值有49个。因此,该模糊神经网络需要训练的参数有wkl,cij和σij。其中,k=1,2,3;l=1,2,…,49;j=1,2,…,7。
3 模糊神经网络PID控制算法仿真实现
3.1 AMESim被控对象模型的建立
本文的阀控缸系统模型由AMESim直观物理图形建模软件建立。如图4所示,设定阀口的体积流量为10 L/min,气缸行程0.12 m,最大静摩擦力为50 N,动摩擦力为40 N,粘性摩擦系数为80 N/(m/s),缸径为0.063 m,环境温度293 K,气源压力0.7 MPa。同时插入交互接口,设定其输入为位移值X,输出为模糊神经网络PID的控制量S并命名为AMESim[8]。因为需要用到MATLAB与AMESim联合仿真,所以AMESim中的模型需要一直运行。

图4 气动系统被控对象模型
由于被控对象的模型由AMESim建立,在MATLAB中以S函数的形式存在,而在MATLAB的Simulink中没有模糊神经网络的模块,需要编写相应的模糊神经网络PID控制器S函数来实现联合仿真。需要将MATLAB与AMESim放在相同目录并且模型具有相同名称[9]。
3.2 仿真分析
在MATLAB环境下搭建模糊神经网络PID对比常规PID控制效果的Simulink仿真模型如图5所示,图中S-Function fnn_pid Controller模块为利用S函数创建的模糊神经网络PID控制器模块,其输出送给被控对象模块AMESim,输入为阶跃信号。
本文中常规PID的参数值由MATLAB/Simulink软件中的Signal Constraint模块优化产生。在已有的Simulink模型中添加一个信号约束模块,将此模块连接到输出信号上,以约束PID控制的输出响应,该模块会自动地将时域约束转换成最优化约束问题。将KP、KI、KD作为寻优参量,添加到工作空间中并设定参数范围,然后使用最优化工具箱Optimization Toolbox中的最优化算法进行求解[10]。设置参数寻优的约束条件为:上升时间1 s,超调量≤20%,调节时间为5 s,误差范围±1%。采用梯度法进行了寻优试验。寻优后的PID参数值为:Kp0=4.257 1,KI0=2.658 7,KD0=0.031 5。
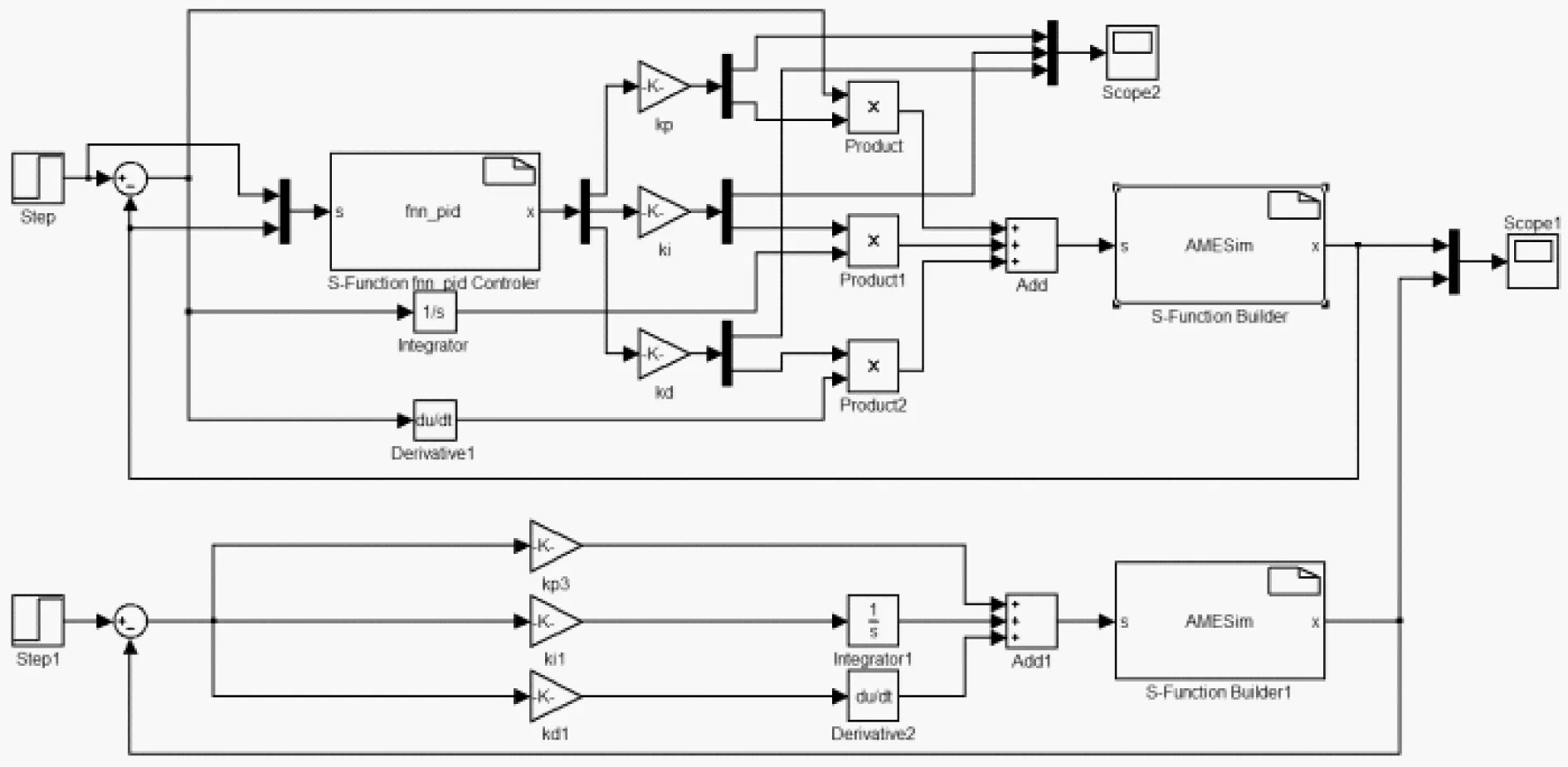
图5 Simulink仿真模型
模型搭建完成后进行仿真实验,nh取为7,学习速率xite=0.2,alfa=0.3。设定系统仿真时间设为10 s,在以上仿真模型的基础上联立两个软件对控制器进行仿真,同时通过观察显示器得到如图6所示两种不同控制器系统的阶跃响应曲线。
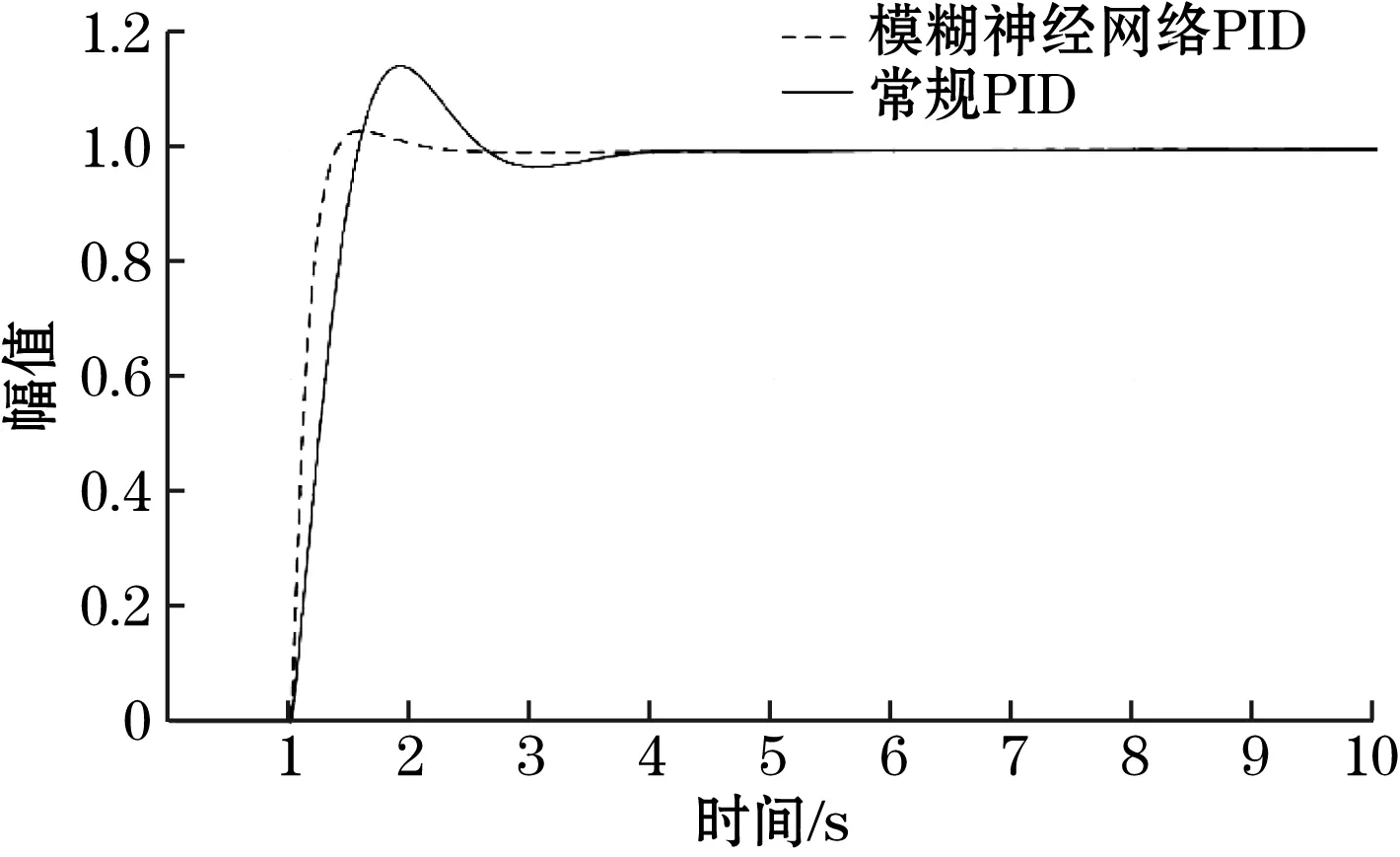
图6 缸径0.063 m阶跃响应曲线
为了验证模糊神经网络PID控制算法的适应性,对被控对象的参数进行调整来模拟更换不同阀门。不同阀门之间最大的差别是气缸大小,通过在AMESim中调整气缸直径可以模拟这一变化,上面仿真所使用的的气缸直径为0.063 m,现在将气缸直径变化为0.05 m和0.1 m,在不改变其他条件的情况下分别进行仿真,可以得到图7和图8两组对比曲线。
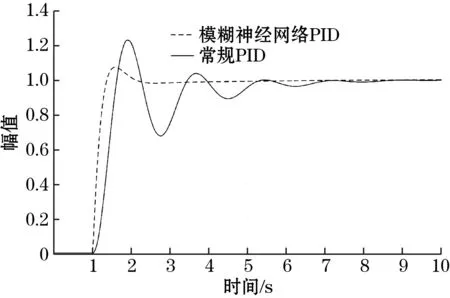
图7 缸径0.05 m阶跃响应曲线
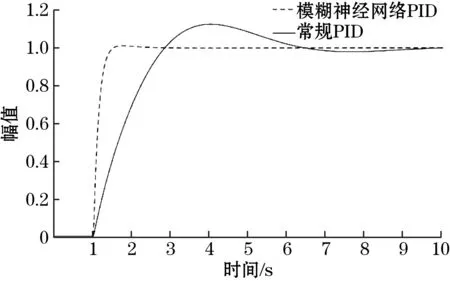
图8 缸径0.1 m阶跃响应曲线
仿真结果表明:在被控对象发生改变时,常规PID由于参数固定,参数不能根据外界环境的变化实时调整,控制效果明显下降,调节时间较长、振荡明显、响应缓慢;而通过引入模糊神经网络来实时调节常规PID的参数,便能很好的提升控制算法应对系统的变化的能力,可以针对被控对象的变化作出调整,在被控对象参数发生明显改变时控制效果几乎不变。模糊神经网络PID算法结合了常规PID控制和模糊控制以及神经网络的优势,实现了对参数的在线整定,可以满足智能定位阀控制系统对阀门开度实时性和精度的控制要求。
4 实验及分析
为验证控制算法的实际控制效果,以STM32单片机为核心搭建了如图9所示的智能阀门定位器作为试验平台,其硬件主要包含单片机最小系统、电源模块、采样模块、电气转换驱动模块以及人机交互模块;软件则用C语言在单片机上进行嵌入式开发,将该控制算法嵌入到单片机中,实现PID参数的自整定。

图9 实验平台
如图10所示为调试过程所用到的实验装置,主要由管道、水泵、水源、气源、阀门以及数据采集系统等组成,可以实现智能阀门定位器在不同管道、不同水压和气压的情况下对不同阀门进行控制的实验过程。

图10 综合测试装置
智能阀门定位器的测试实验在完全模拟现场工况的情况下进行,通过前期各个环节的测试后,设定了如表1所示的设备参数。
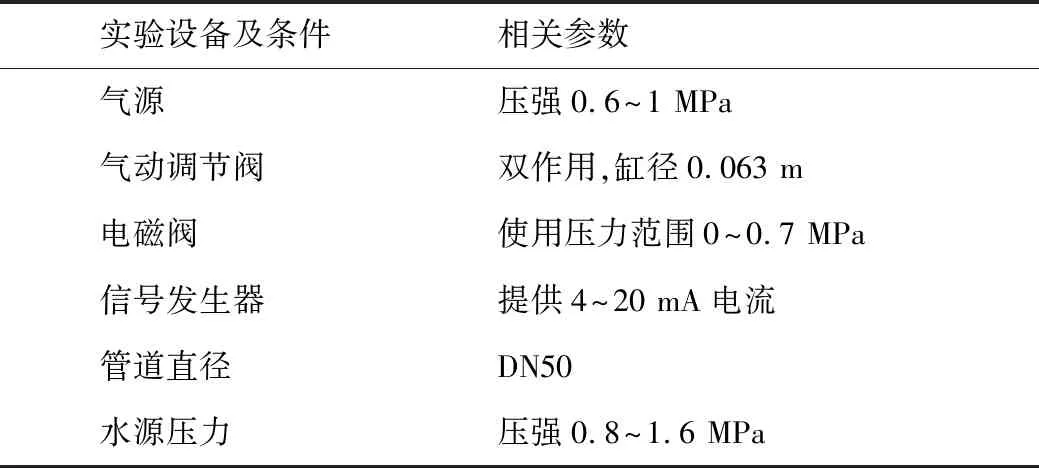
表1 系统实验设备相关参数设置表
实验过程首先需要打开气源和水源,并将输出气源压力调整到0.6 MPa,水源压力调整到0.8 MPa,然后通过调节信号发生器对系统施加不同的开度控制指令,同时利用采集系统采集并记录相应数据。实验主要针对控制精度进行相应的测试,为了探求不同工况下系统控制精度的大体分布范围,实验中主要测试了开度分别为0%、25%、50%、75%、100%的5个特征点,同时在每个点的测试中设置水源压力范围为0.8~1.6 MPa,每间隔0.2 MPa测试一组数据,每个点共测试并记录5组数据,实验过程所采集到的数据如表2所示。
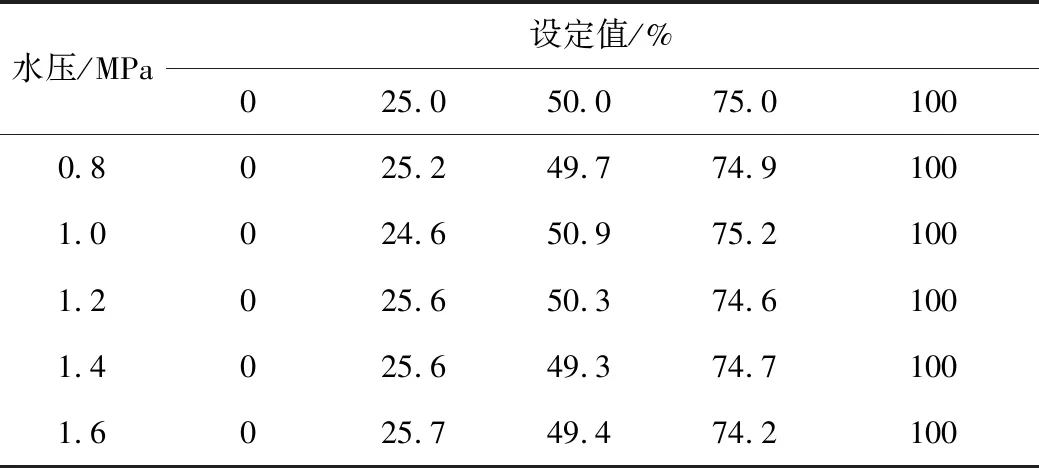
表2 不同水压下阀门开度测试结果
通过多次实验数据可知:系统响应较快,控制过程较为平稳,系统控制精度能达到1%;同时系统可以根据不同的工况需求进行相应的设定,以发挥不同特性之间的响应优越性;在控制过程中系统不存在执行器振荡过冲等现象,系统能够实现对阀门位置的控制,满足实际要求的性能指标。
5 结束语
本文提出了一种基于模糊神经网络的阀位控制算法,阀控缸系统由于气体可压缩性以及动静摩擦力等因素具有较强的时变、非线性特性。采用模糊神经网络整定PID参数的方式可以有效提升系统的适应性和抗干扰能力。仿真分析表明;该控制算法在被控对象发生改变时可以及时对PID参数做出调整,控制效果基本不变。实验数据说明:系统在不同水压下的控制精度都小于1%,且响应快速,过程平稳,满足阀位控制要求。
