基于时栅传感技术的带检测功能直线导轨
2019-03-28毛阿敏彭东林王阳阳徐志伟
毛阿敏,彭东林,王阳阳,徐志伟
(重庆理工大学,机械检测技术与装备教育部工程研究中心,时栅传感及检测技术重庆市重点实验室,重庆 400054)
0 引言
为了适应现今机械高速度、高精度、节能等要求,直线导轨已得到广泛应用和迅速发展[1-2]。对直线导轨的研究正趋于智能化、集成化、模块化[3]。智能化的直线导轨是将导轨和编码器整合,使其兼具直线导引和位置回馈功能,实现高精度定位,可广泛应用于数控加工中心、机械手臂、自动化设备等需要精确定位的传动机构系统中。市场上应用较多的高精度导轨单元一般采用磁栅技术构建检测系统。其中,由瑞士SCHNEEBERG研制的Monorail带磁栅测量系统的滚动直线导轨副,就是通过将导轨的导向功能和磁栅的位移检测功能相结合,实现运动中导轨滑块运动位置信息的实时反馈[4]。中国台湾上银科技公司的IG智能型直线导轨采用导轨与磁性编码器于一体的结构,将直线导轨与编码器整合[5]。磁栅直线导轨因兼有测量系统、磁栅热变形小、测量精度高等特点应用于高端机床位置测量领域[6]。然而,由于技术手段以及使用环境条件的限制,磁栅导轨的磁膜易受损,尤其在经常使用强磁性表座的场合,存在消磁的风险,因此使其应用受限。
时栅是一种以时间量作为测量基准,通过高频时钟插补技术来实现高精度测量的新型位移传感器[7]。由于采用时间基准,因此无需精密的刻线技术,在普通机械加工工艺下即可达到较高的测量精度,适用于复杂工况,可靠性高[8-9]。本文在文献[10]的研究基础上,提出一种将时栅的定尺嵌入导轨平面的凹槽内,动尺测头与滑块固联,集成测量系统与被测系统的带检测功能直线导轨,以实现导轨的智能化。
1 工作原理
1.1 结构设计
滚动直线导轨是以滚珠作为导轨和滑块之间的动力传输界面,通过其无限滚动循环运动驱动滑块沿导轨作高速高精度直线运动。在一般工业场合,导轨的部分上表面不承受负载,因此设计带检导轨的结构如图1所示。在不损坏滚珠滚道的前提下,通过在导轨上表面加工凹槽,再将时栅的定尺嵌入凹槽内部,实现导轨和定尺的集成。时栅的动尺通过联接板与导轨滑块固联,实现与滑块的同步运动。
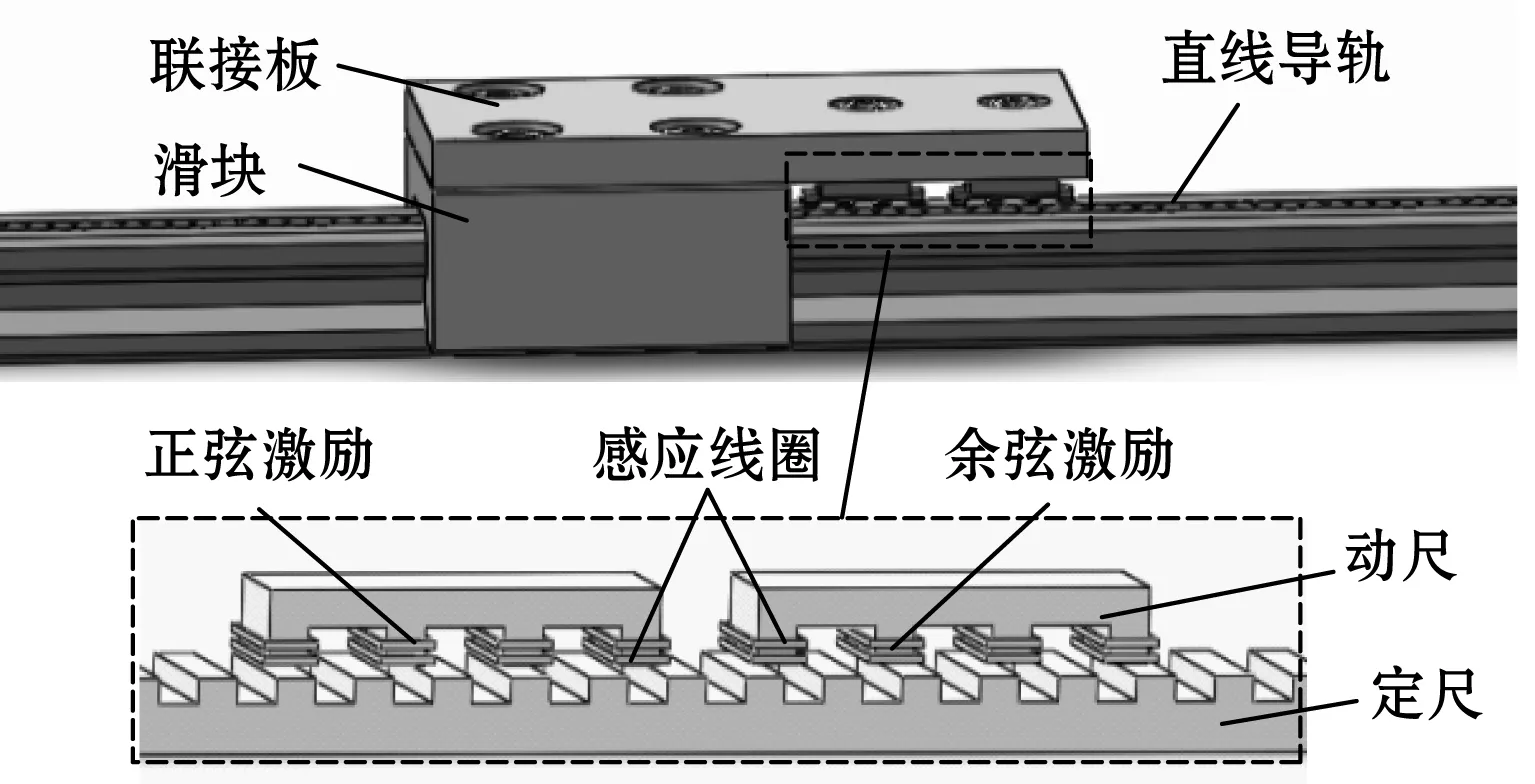
图1 带检导轨结构
时栅定尺上分布有等间距的齿槽,动尺由结构相同的两个导磁铁芯A、B构成,激励线圈与感应线圈均位于动尺。A、B测头分别绕制正、余弦激励线圈,其绕向为正-反-反-正串联,感应线圈绕向为正-正-反-反串联,如图2所示。同时,A、B两相测头初始位置错开W/4,以实现空间正交。

图2 时栅结构及线圈绕向
1.2 测量原理
动尺上的激励线圈和感应线圈与定尺周期变化的齿槽形成完整磁路。当时栅动尺相对定尺运动时,动定尺之间的气隙磁导周期变化引起磁路磁通周期性变化。由于气隙磁导高次谐波的幅值远小于基波幅值,可以只考虑气隙磁导变化中的恒定分量和基波分量,则A、B测头各齿下的磁导变化规律为:
式中:Λ0为气隙磁导恒定分量;ΛM1为气隙磁导基波分量幅值;W为极距;i为动测头齿号,i=1,2,3,4。
激励线圈与感应线圈之间的互感抗与气隙磁导具有相同的变化规律:
在A测头激励线圈通入电流iA=Imsinωt,在B测头激励线圈通入电流iB=Imcosωt。考虑电流正-反-正-反的方向,每个齿下的电流依次为:
iAi=(-1)i-1Imsinωt
iBi=(-1)i-1Imcosωt
则各感应线圈的输出电势依次为:
eAi=iAi·XAi
eBi=iBi·XBi
则A、B测头感应的驻波信号分别为:

将两驻波信号串联输出,可得到测量所需的行波信号:
E=Km(EA+EB)


式中Km为磁场耦合系数。
为了对感应电信号进行提取、变换、分析,设计了传感器后续信号处理电路,如图3所示。感应的行波信号经过信号调理电路进行放大、滤波、整形,转换成方波信号并送入比相电路,与参考信号进行比相,然后利用高频时钟脉冲插补两信号的相位差,得到输出信号与参考信号的时间差Δt,再通过如下关系式运算可得到动尺位移量:
式中N为动尺相对于定尺移动的完整极距数。

图3 信号处理示意图
2 模型建立与仿真分析
2.1 模型建立
以不影响滑块内滚珠与导轨的接触面为基本原则,导轨表面凹槽的宽度应小于上表面的最小宽度,从而确定嵌入的定尺的宽度。为了减小漏磁通影响,增强信号强度,动尺的宽度应略小于定尺宽度。在三维软件中建立如图1中的带检导轨模型,并导入Ansoft Maxwell软件进行仿真,以便于后续对模型的优化,节省了模型的建立和优化时间,提高研究效率。模型参数设置如表1所示。

表1 仿真模型参数
2.2 仿真分析
Ansoft Maxwell软件是一款电磁场仿真软件,具有强大的求解功能。其三维瞬态磁场模块可以计算三维模型的瞬态工作过程。
在仿真中设置动定子的材料为steel1008,线圈材料copper;A、B测头激励信号分别为IA=0.1sin(2π·40 000t)A,IB=0.1cos(2π·40 000t)A;划分网格时,线圈网格的最大边长设置为0.2 mm,动定尺铁芯设置为1 mm,真空设置为5 mm;动尺运动一个空间极距为4 mm,运动步距为0.1 mm。
感应线圈输出电势仿真结果如图4所示,输出的感应电势为一组初相角不同的正弦信号。由于初相角与动尺的位移线性对应,需要通过对感应电势的初相角进行解算来获得动尺的位移量。对行波信号中每一条正弦曲线运用傅里叶变换计算其初相角,由于一个2π周期对应一个极距W,因此初相角可以转换成对应的直线位移量,将计算结果与理论位移作差即得到位移误差值[11]。为了分析位移误差中各次谐波成分,以便针对不同频次谐波进行抑制,需要通过对位移误差数据进行快速傅里叶变换,从而可得到位移误差中的各次谐波分量。

图4 感应线圈输出电势
2.3 模型优化
为了减小模型误差并消除气隙磁导谐波分量的影响,且为了使气隙磁导变化规律接近正弦形,将定尺的齿型选择正弦齿型,形状由式(1)确定,A、B为齿形系数,选择A为4,B为4/3,动尺结构不变,建立如图5所示的模型并进行有限元分析,仿真参数设置同上。
(1)
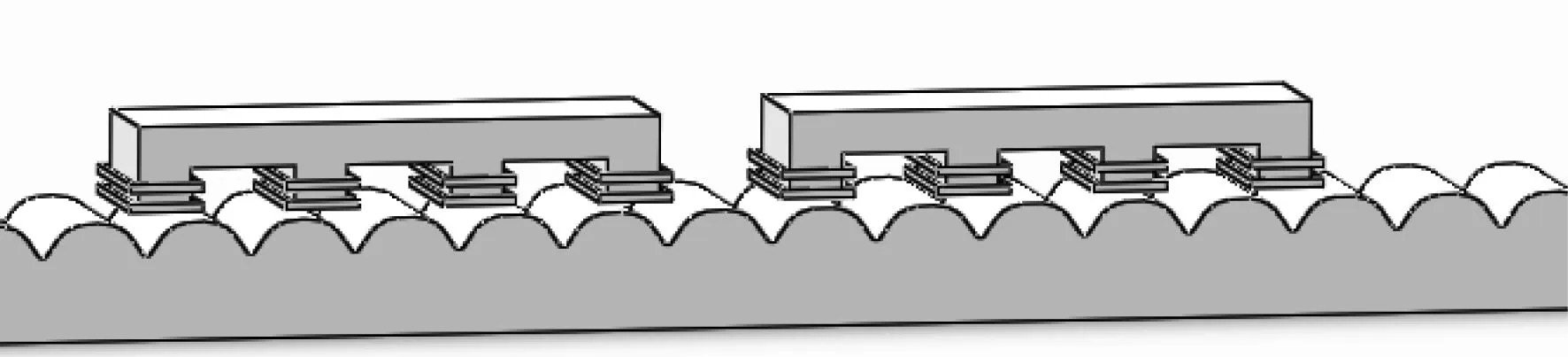
图5 优化后传感器模型
模型改进前后位移误差大小如图6所示,模型改进前后位移测量总误差由原模型的-60~60 μm下降到-18~20 μm。对位移误差进行快速傅里叶变换得到误差频谱,如图7所示,由图7可得,模型改进后各次误差的幅值均有所降低且均处于μm级,尤其2次、4次误差降低了75%左右。但由于两相测头之间的漏磁通产生残留电压信号,因此仿真结果中还存在较大的1次误差,后期可以通过硬件补偿即通入一路补偿信号来减小残留电压。此外,网格划分不均、计算精度等都会引入一定误差。

图6 模型改进前后1个极距内动尺位移误差

图7 模型改进前后位移误差频谱
3 实验验证
根据仿真分析的结果,采用慢走丝线切割工艺加工如图8所示的定尺和动尺,其中动尺上励磁线圈和感应线圈手工绕制,匝数分别为20匝、60匝,如图8(a)所示,定尺总长250 mm,如图8(b)所示。

(a)动尺

(b)定尺图8 动尺和定尺
为验证仿真结果,搭建了如图9所示的实验平台以进行实验验证。将导轨固定在大理石平台上;导轨滑块与直线电机相连,电机驱动滑块滑动。实验平台的测量基准选择RENISHAW ML80激光干涉仪。

图9 实验平台
当电机驱动滑块滑动,即动尺相对定尺运动时,下位机对时栅带检导轨和激光干涉仪的位移进行实时监测,并通过串口发送于上位机进行显示。两测量值之差即为带检导轨原始误差。图10为滑块滑动1个空间极距的误差曲线。
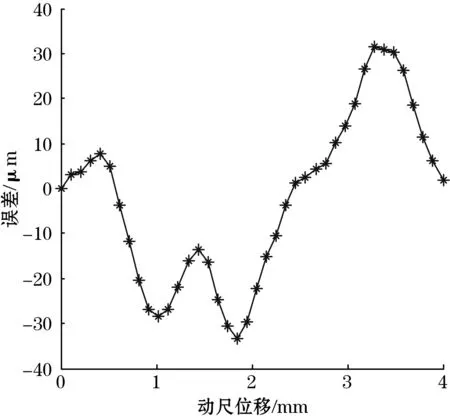
图10 1个极距内位移测量误差
由图10可得,原始误差的峰峰值为64 μm,其中存在较大的1次、2次和4次误差。其中1次误差是由A、B两测头之间的漏磁通引起;2次误差是由两测头感应电势的幅值不等、相位不完全正交引起;4次误差是由动定尺齿槽的齿谐波引起的。此外,动定尺的加工误差、安装误差以及外界信号干扰等都会对总误差产生影响。
通过误差补偿,在一个极距内测量误差峰峰值为0.66 μm,如图11所示。在200 mm测量范围内,测量误差的大小为1.25 μm,如图12所示。

图11 补偿后1个极距内位移测量误差
4 结论
本文结合时栅传感技术提出了一种带检测功能直线导轨的设计方案,并开展了模型的仿真、分析、优化、实验平台的搭建及实验验证等工作,得出以下结论:

图12 补偿后200 mm内位移测量误差
(1)通过将时栅技术嵌入直线导轨,实现测量系统与被测系统的集成,使导轨导引同时进行位置反馈,实现了直线导轨副的闭环控制功能。
(2)通过进行精度实验,带检导轨的测量精度达到1.25 μm,实现了高精度测量,可满足一般工业现场的需求。
