基于MPSO-BP神经网络的PSD误差补偿

王福杰，俞恒杰，陆辉山

(中北大学机械工程学院，山西太原 030051)

0 引言

PSD(Position Sensitive Detector)是一种能在感光表面连续移动光点位置的光电子传感器，属于位置敏感检测器，广泛应用于光学位置和角度的测量与控制、位移和振动监测、激光光束校准、自动范围探测系统以及人体运动及分析系统等。然而，由于敏感层电阻不均、电极结构差异以及边缘效应等因素，PSD存在较大非线性误差[1]，使其输出坐标不能正确地反映入射光点的实际位置。

孙淑光、王天游[2]等基于压电执行器的精密刀具伺服系统精确测量平移滑块的整体直线度误差，实现对PSD输出结果的误差补偿；A.Saha，S.Das，M. Suresh[3]等将微机电系统数字加速度计集成在安装二维PSD的同一平台上，以消除自振的影响；S. Regnier，S. Haliyo等[4]提出了一种非线性标定方法将正常位置电压响应的灵敏度误差控制在3.6%以内。通过组建硬件系统对误差进行补偿的方法对系统的要求高，非线性标定的算法需要得到电压相关灵敏度的连续函数。软件补偿方法有模拟退火方法、差分进化算法、BP神经网络等。陈盛，赵东标，陆永华等[5]采用模拟退火算法对螺纹参数测量误差进行修正，但它的初始温度要高、终止温度要低、降温速率要慢，且抽样数目多，因此优化过程较长；呼静静，李国勇等[6]采用差分进化算法辨识直线电机的摩擦模型参数,原理简单，受控参数少，但随着迭代次数的增加，个体间的差异会逐渐减小，影响变异的多样性；Z. Sun，Q. Song等[7]利用反向传播(BP)神经网络来补偿二维 PSD的非线性误差，但它的收敛速度仍旧非常缓慢，进入局部极小的情况仍旧很多。

本文在现有研究的基础上，利用改进的粒子群算法(Modified Particle Swarm Optimization，MPSO)优化后的人工神经网络模型对PSD输出的非线性误差进行补偿。与 BP 神经网络对比，进一步表明改进 MPSO-BP算法在非线性误差补偿上的优越性。

实验中建立了基于高灵敏度光电位置传感器(PSD)的光电测试系统，测量并记录已知角度下的系统输出的电信号；通过设计三层 BP神经网络模型，以MPSO 算法在多源传感数据样本集上确定模型连接权值和阈值，之后将训练好的 MPSO-BP 神经网络用于PSD输出误差的补偿，最后在测试集上对 MPSO-BP 算法的收敛速度和识别准确率进行了分析，并同现有方法做了比较。

1 MPSO-BP神经网络模型

1.1 粒子群算法

(1)

由于PSO中粒子都向最佳位置聚集，会形成粒子种群的快速趋同效应，容易陷入局部最优和过早收敛现象[10]。

1.2 改进的粒子群算法

为了克服上述不足，分别对惯性因子和学习因子做出改进[9-12]。在优化初期，ω取为较大值，增强全局寻优能力，这样有利于跳出局部极小，而随着优化过程的不断推进，ω应逐渐减小，这样有利于增强局部搜索能力，提高算法的收敛速度。故采取线性递减惯性因子：

(2)

式中：ωmax为初始惯性因子；ωmin为最终惯性因子；itermax为最大迭代次数；iter为当前迭代次数。

学习因子的大小决定了粒子自我认知和社会认知对粒子的影响，为了防止陷入局部最优，可以通过动态地改变c1和c2来保持粒子始终具有多样性。优化后的算法在初期使粒子具有大的自我认识(大的c1)和小的社会认知(小的c2)，便于快速搜索；在算法后期，应有小的自我认知(小的c1)和大的社会认知(大的c2)，加快算法收敛和在全局范围内寻找最优解。对此有如下改进：

(3)

式中：cst和cend分别为c1的初始值和最终值。

1.3 MPSO-BP神经网络

BP神经网络是一种采用误差反向传播训练算法的多层前向神经网络，其理论依据坚实、推导过程严谨、物理概念清晰、通用性强，具有较强的自学习能力，能够解决非线性模式识别问题。

多层前向神经网络的输入与输出之间的关系，可以看成是一种映射关系，这种映射是一个高度非线性映射，如果输入节点数为N，输出节点数为M，网络是从N维欧氏空间到M维欧氏空间的映射。这种映射是通过输入层与隐层之间的传递函数(作用函数或激活函数)，以及隐层与隐层之间，隐层与输出层之间的传递函数将各层的输入经传递函数作用后输出来实现的[3]。其结构图见图1所示。

据此建立三层神经网络结构模型：输入层节点数N个，隐层节点数S个，输出层节点数M个。目前，传递函数的选择常用的是3种Sigmoid函数[4]：log-sigmoid函数、tansig函数、purelin函数。

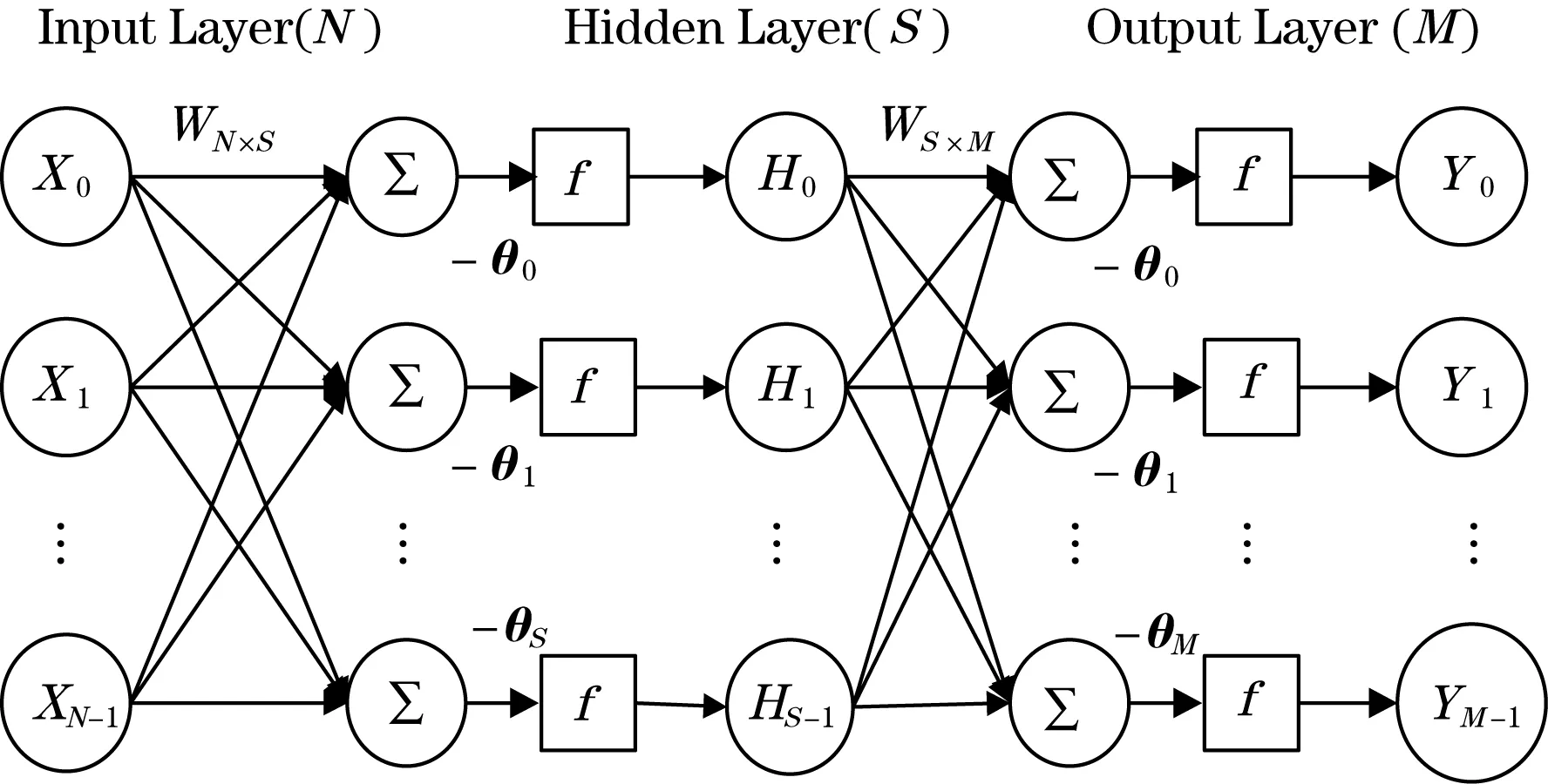
图1 BP网络结构

MPSO-BP神经网络的具体实现流程如图2所示。

图2 MPSO-BP算法流程

2 基于PSD的测试系统的标定

建立了基于PSD的光电测试系统。实验之前，对系统进行标定：用高精度的经纬仪代替物体，旋转经纬仪产生类似物体扰动的角位移，测量并记录已知角度下系统输出的电信号。标定角位移如图3所示，在标定角位移下的电压输出如图4所示。

图3 标定的水平和垂直角位移

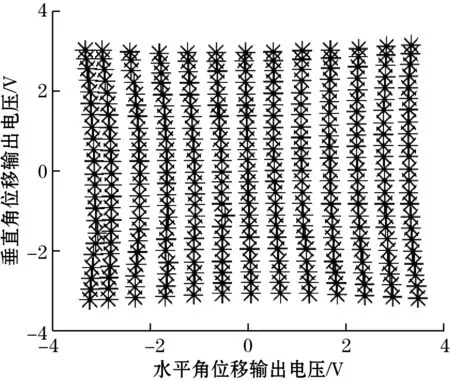
图4 标定输出的电信号

理论上，输出电压和水平角位移成线性关系；输出电压和垂直角位移成线性关系。但是实际由于各种因素影响，从图3和图4可以看出，被测量与输出结果出现非线性偏差。

本文根据一组角位移坐标对应一组电压坐标的关系，采用MPSO-BP神经网络将电压坐标映射到角位移坐标。根据该方法将实验所测得的电压值转化为对应的角位移。

3 BP网络模型的建立及实验数据分析

根据标定数据，建立一个2×35×2的BP网络模型。输入层神经元2个，隐含层35个神经元，输出层2个神经元。传递函数采用sigmoid函数：第一层采用tangsig函数，第二层采用purelin函数。无偏移向量θ。网络设计训练目标误差为0.000 1，粒子最大速度为0.5，初始惯性因子为0.9，最终惯性因子为0.3，c1的初始值为1、最终值为3，最大迭代次数为200。实验采用动态信号测试分析系统DH5920进行测试数据记录。

3.1 模型建立与误差对比

实验首先测得299组数据(水平角位移电压值、垂直角位移电压值)并进行人工标定，标定后得到标准的水平角位移和垂直角位移。将这299组数据分别作为BP神经网络和PSO-BO神经网络的训练样本，随机选取其中240组数据(80%)用作模型的训练，其余59组数据用作模型的测试，比较训练结果。算法训练目标是使得网络输出和期望输出的误差平方和达到最小，适应度函数为

(4)

为更好的体现误差相对于标定数据的偏差程度，将网络输出和期望输出的误差平方和的算术平均值作为评价模型的误差指标，即

(5)

BP神经网络与MPSO—BP神经网络的输出误差对比如图5和图6所示。

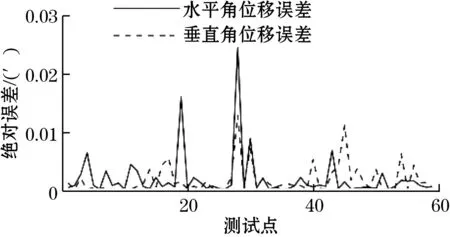
图5 BP神经网络角位移误差

图6 MPSO-BP神经网络角位移误差

为验证算法的特性，分别使用BP神经网络、MPSO-BP神经网络对训练样本进行100次模型建立与测试，分别计算平均误差，如表1所示。

从误差的对比可以看出，MPSO-BP神经网络的水平角位移误差为BP神经网络水平角位移误差的7.3%，其垂直角位移误差为BP神经网络水平角位移

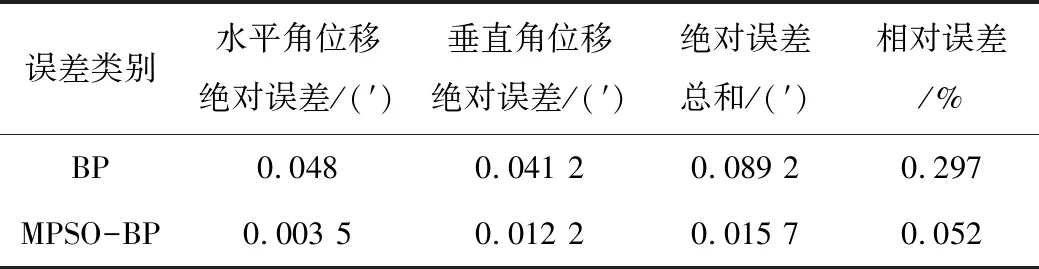
表1 100次测试的平均误差统计

误差的29.1%，其绝对误差总和为BP神经网络水平误差总和的17.6%；相比于BP神经网络0.297%的相对误差，MPSO-BP神经网络的相对误差减小0.052%，准确度提高5倍以上。

3.2 未标定数据补偿

将MPSO学习训练好的网络权值矩阵用于该系统信号分析处理，实验采样频率200 000 Hz，记录时间0～5.24287 s，数据分析时间段为0～0.066 82 s。试验获得的电信号如图7和图8所示，共13 366组数据。

图7 试验水平角位移电压值

图8 试验垂直角位移电压值

经过MPSO-BP神经网络转换处理后的角位移如图9和图10所示。

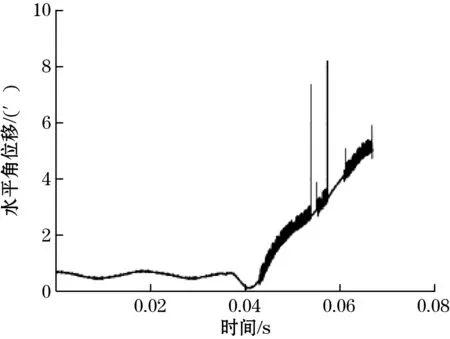
图9 转换后的水平角位移

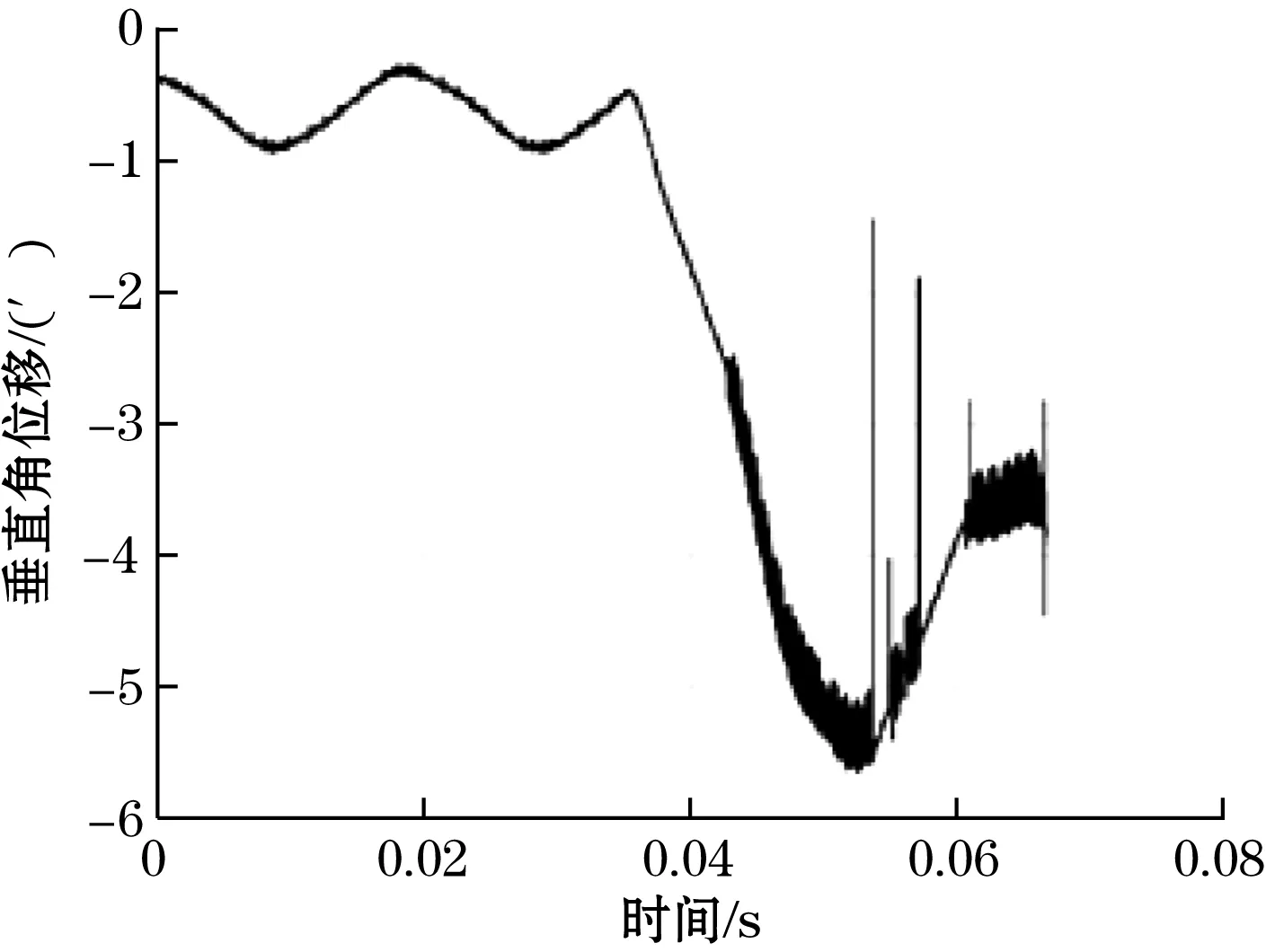
图10 转换后的垂直角位移

特别地，为了增强对比性，图中未将0.055 s后的畸变信号剔除。对比图7和图9，以及图8和图10：很明显地，MPSO-BP神经网络处理后，角位移数据保持了原电信号数据的特征，保持了数据的一致性。

4 结束语

本文针对光电位置传感器测试系统的输出非线性问题，提出了采用改进粒子群算法和BP神经网络对输出结果进行补偿修正。将优化后的初始值代入神经网络中进行训练，加快学习速率、克服陷入局部最优的情况，同时提高识别准确率。试验结果表明：该方法有很好的容错和泛化能力，能有效降低PSD测试系统本身及环境对测量精度的影响。