金属壳谐振陀螺温度误差补偿方法
2019-03-28万承军
杨 锐,苏 中,万承军,王 楚
(1.中国久远高新技术装备公司,北京 100094;2.北京信息科技大学,高动态导航技术北京市重点实验室,北京 100101;3.北京航天长征飞行器研究所,北京 100076)
0 引言
金属壳谐振陀螺是振动陀螺的一个重要分支,其敏感结构为金属谐振子,当谐振子随载体旋转时,哥氏效应引起敏感结构振型的“移动”是其对“旋转”敏感的基本表现形式[1]。金属壳谐振陀螺具有结构强度高、抗过载能力强的优点,在兼顾抗过载、量程和精度上表现出显著潜力[2-3],而其余振动陀螺的振动部件均不能适应大过载环境[4]。
金属谐振子的加工工艺相对简单、成品率高、易于实现[5]。但金属材料本身具有较大的温度系数和热膨胀系数,受环境温度变化影响明显[6]。因此,对金属壳谐振陀螺的温度特性进行研究,并利用温度模型进行补偿以提高陀螺精度是非常有必要的。
本文通过对金属壳谐振陀螺温度误差机理进行分析,提出金属壳谐振陀螺温度误差补偿方法,采用线性模型和玻尔兹曼模型对金属壳谐振陀螺的温度误差进行补偿。经实验验证,基于玻尔兹曼模型的补偿效果优于基于线性模型的补偿效果。本文中的金属壳谐振陀螺为北京理工大学和北京信息科技大学研制的钟形振子式角速率陀螺[8]。
1 温度误差机理分析
对于金属振子而言,在温度发生变化时,由于材料的弹性模量、热膨胀系数、阻尼系数以及振子的质量偏差等因素的存在,会使振子内部产生非均匀的热应力,并且随温度的变化而变化,从而导致谐振频率、频率裂解、振型偏移的改变,对谐振子的振动特性产生影响[9]。
在材料弹性模量变化和热应力作用下,谐振子刚度随温度变化的关系可表示为[10]
K=K0[1+(kt+λσaE0)(T-T0)]
(1)
式中:K、K0分别为谐振子在温度T、T0时的刚度;kt为弹性模量随温度变化的系数;λσ为热应力引起的谐振子刚度变化的比例系数;a为热膨胀系数;E0为谐振子材料在温度T0时的弹性模量。
由此,可得到金属谐振子的谐振频率与温度的关系[11]:

(2)
式中f(T)、f0分别为谐振子在温度T、T0时的谐振频率。
由式(2)可知,当温度发生变化时,由于金属壳谐振陀螺的谐振频率发生变化,陀螺输出精度降低。
2 零偏-温度模型
零偏-温度模型指根据陀螺各温区的零偏数据,通过拟合建立零偏与温度之间的数学模型。基于该模型,陀螺可实时计算由于当前环境温度造成的陀螺输出漂移,在陀螺输出中扣除该漂移即可达到陀螺温度误差补偿目的。
2.1 线性模型
线性模型是金属壳谐振陀螺进行温度误差补偿的经典模型,基于该模型的零偏-温度关系如下:
B(T)=a1T+a0
(3)
式中:B(T)为陀螺零偏输出;a1、a0为拟合系数;T为温度。
2.2 玻尔兹曼模型
基于玻尔兹曼模型的零偏-温度关系如下:

(4)
式中:A1,A2,T0,d为拟合系数。
3 零偏-温度数据分析与补偿
将由3支金属壳谐振陀螺(量程:±3 600°/s)组成的惯性测量单元静止置于温箱内,X轴朝上,设置温箱温度变化范围为-40~60 ℃,陀螺上电并记录数据,采样频率50 Hz,采样时间3 h。将惯性测量单元的Y轴、Z轴分别朝上,重复上述实验。
由实验结果得到X轴陀螺、Y轴陀螺、Z轴陀螺零偏与温度之间的关系如图1所示。由图可知,X轴陀螺、Y轴陀螺、Z轴陀螺的零偏值受到温度变化的影响都很大,随着温度的升高,X轴和Y轴陀螺的零偏值越来越小,Z轴陀螺的零偏值越来越大,X轴陀螺、Y轴陀螺和Z轴陀螺的最大偏移误差分别为13.742 1°/s、17.350 4°/s和19.439 9°/s。

(a)

(b)
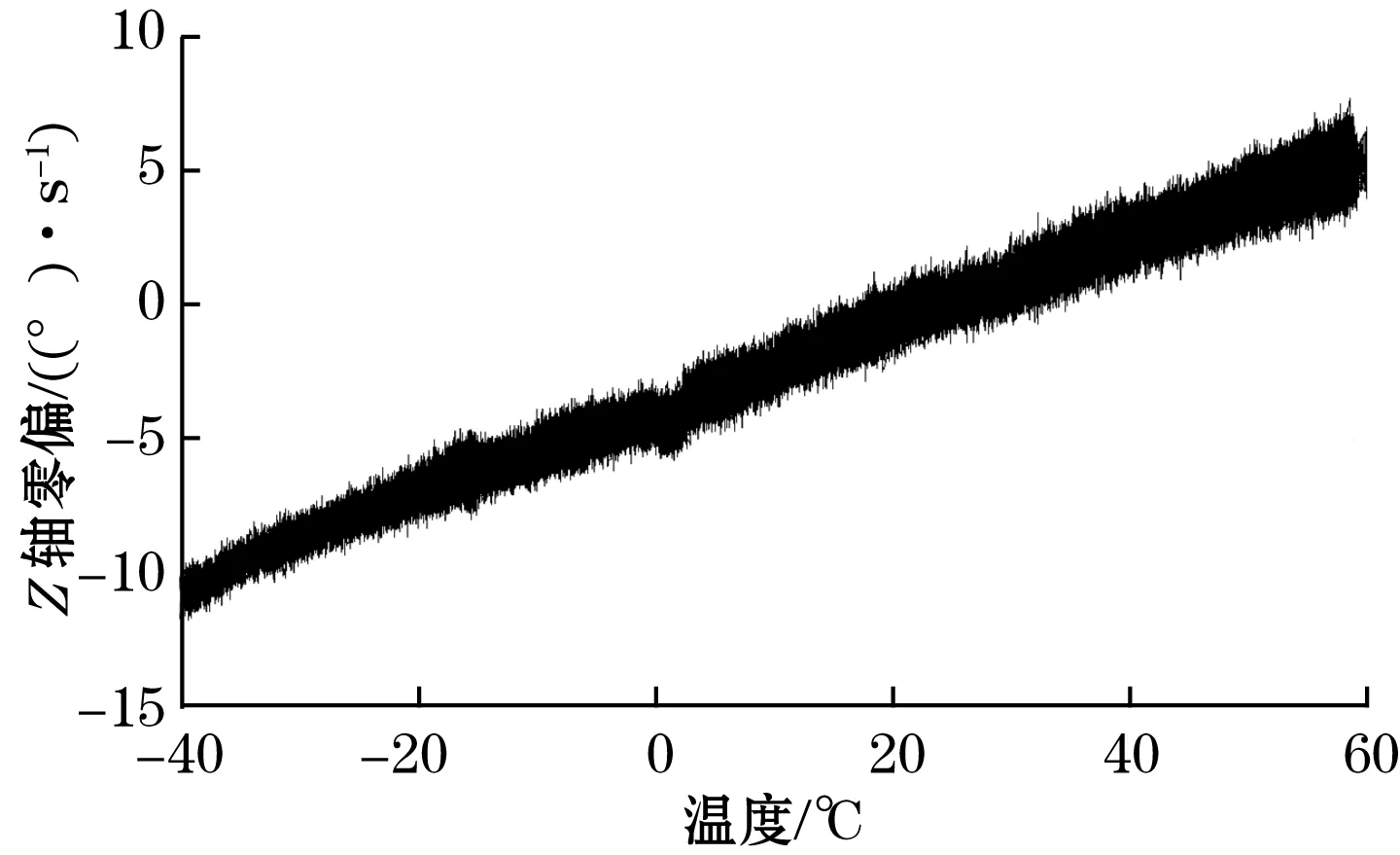
(c)图1 X、Y、Z轴陀螺零偏和温度关系
取实验数据中-40 ℃、-30 ℃、-20 ℃、-10 ℃、0 ℃、10 ℃、20 ℃、30 ℃、40 ℃、50 ℃和60 ℃温度点对应的陀螺零偏数据,得到温度与X、Y、Z轴零偏关系数据如表1所示。

表1 温度-X、Y、Z轴零偏关系数据表
分别对温度T和随温度变化的X轴陀螺零偏Bx(T)、Y轴陀螺零偏By(T)、Z轴陀螺零偏Bz(T)进行线性拟合和波尔兹曼拟合。X轴、Y轴和Z轴零偏数据拟合效果相似,以X轴零偏数据为例,拟合得到零偏-温度的线性模型为式(5),玻尔兹曼模型为式(6):
Bx(T)=-0.095 9T+2.688 2
(5)
(6)
X轴陀螺的零偏-温度关系的线性拟合和玻尔兹曼拟合效果对比结果见图2,X轴、Y轴、Z轴陀螺拟合残差对比结果见图3、图4和图5。
由拟合效果对比和拟合残差对比图可看出,基于玻尔兹曼模型的零偏-温度关系拟合效果优于基于线性模型的拟合效果。

图2 X轴零偏-温度关系拟合效果对比
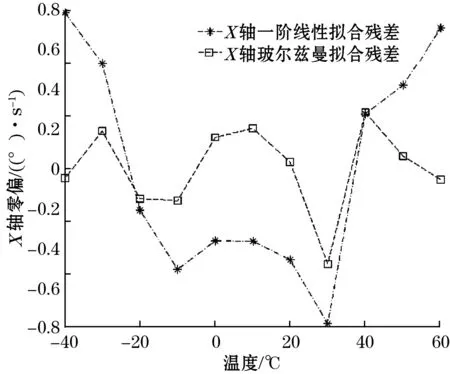
图3 X轴零偏-温度关系拟合残差对比
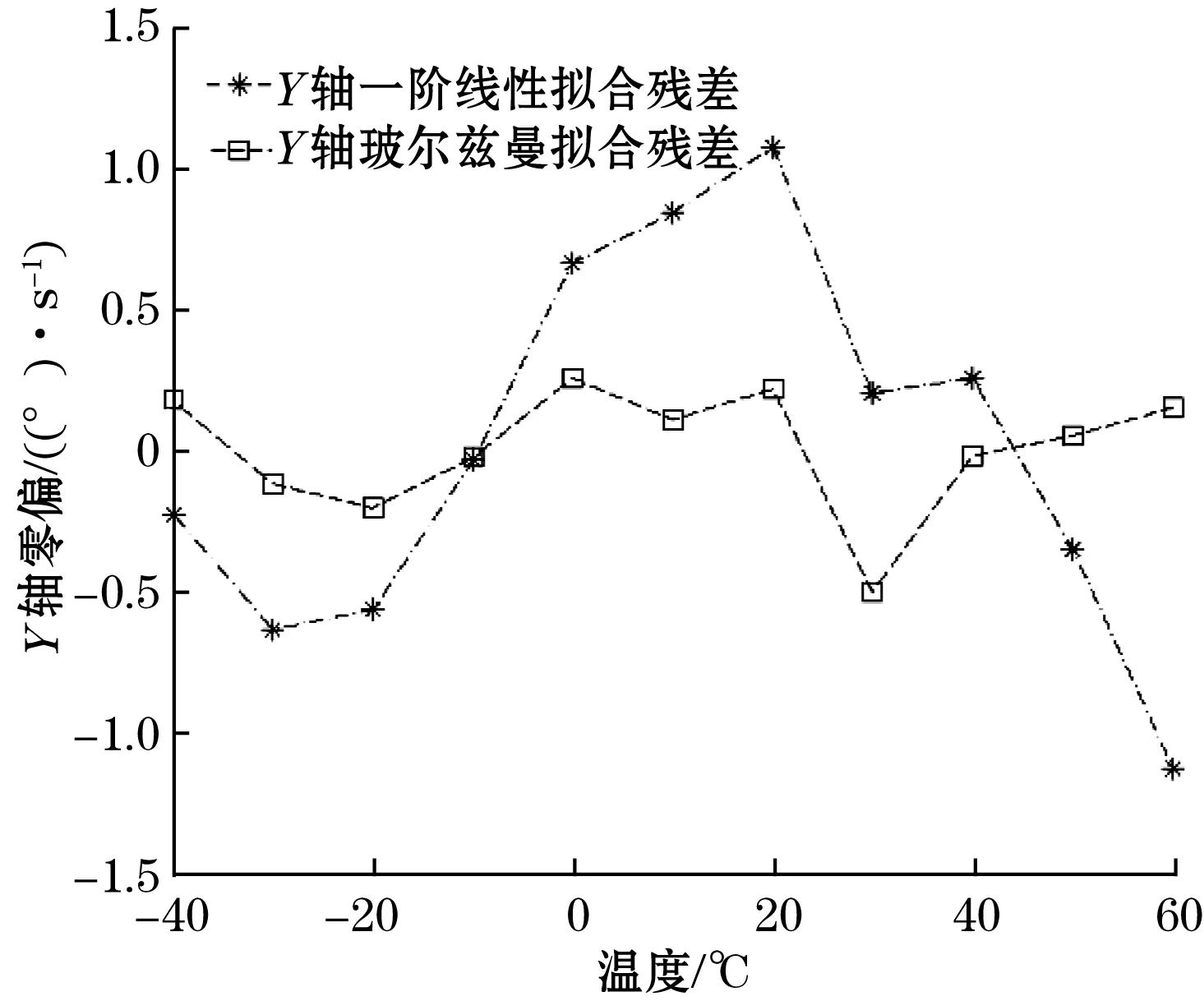
图4 Y轴零偏-温度关系拟合残差对比

图5 Z轴零偏-温度关系拟合残差对比
利用零偏-温度模型对陀螺进行温度补偿,补偿后的陀螺输出为
Gc(T)=G(T)-B(T)
(7)
式中:G(T)为陀螺原始输出;B(T)为基于零偏-温度模型计算的补偿量,即基于零偏-温度模型计算得到的陀螺零偏输出。
基于建立的线性模型和玻尔兹曼模型,分别对金属壳谐振陀螺全温区的零偏数据进行补偿。基于玻尔兹曼模型的X轴陀螺、Y轴陀螺和Z轴陀螺零偏补偿前后效果见图6、图7和图8。

图6 X轴零偏-温度的玻尔兹曼模型补偿效果
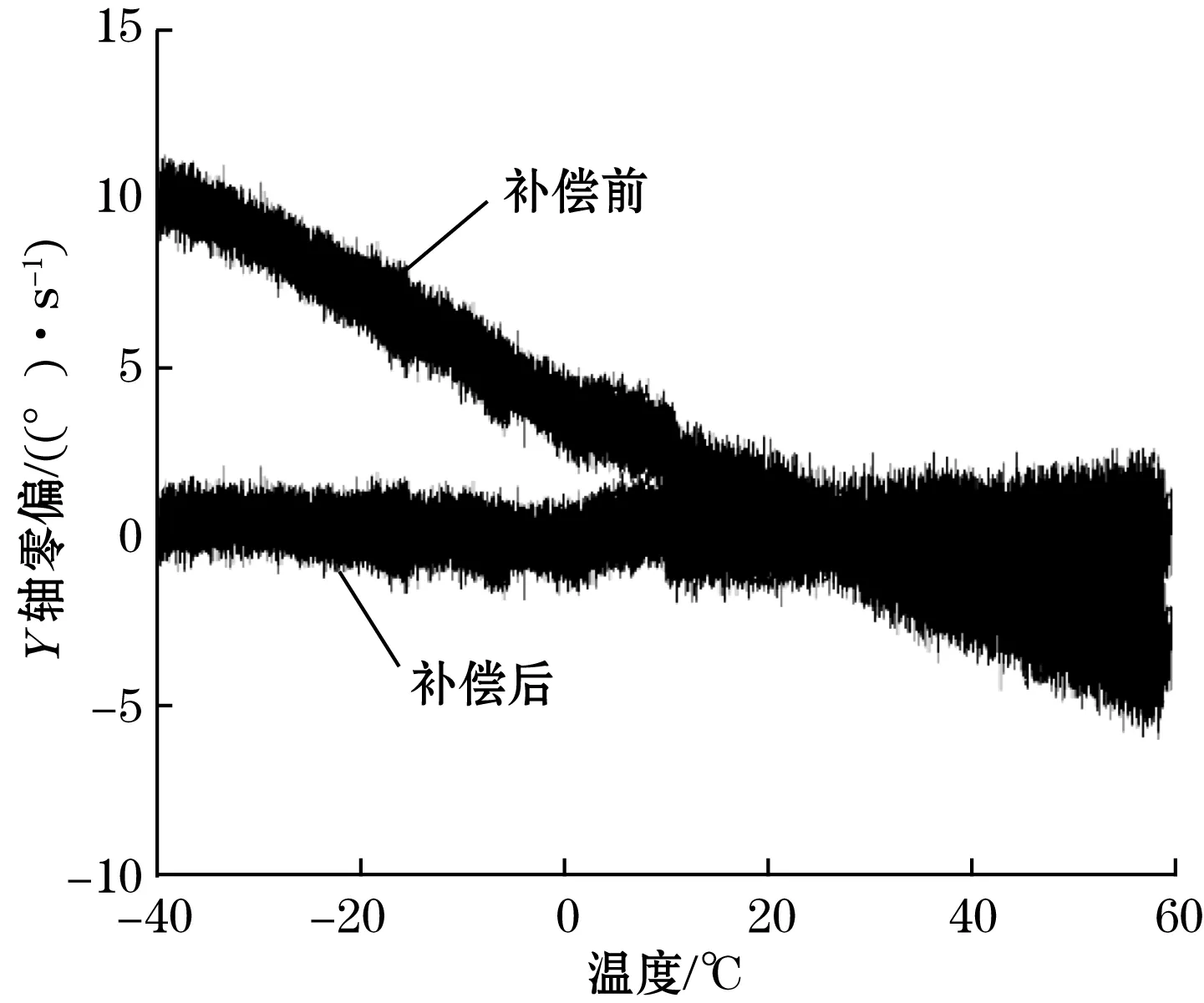
图7 Y轴零偏-温度的玻尔兹曼模型补偿效果
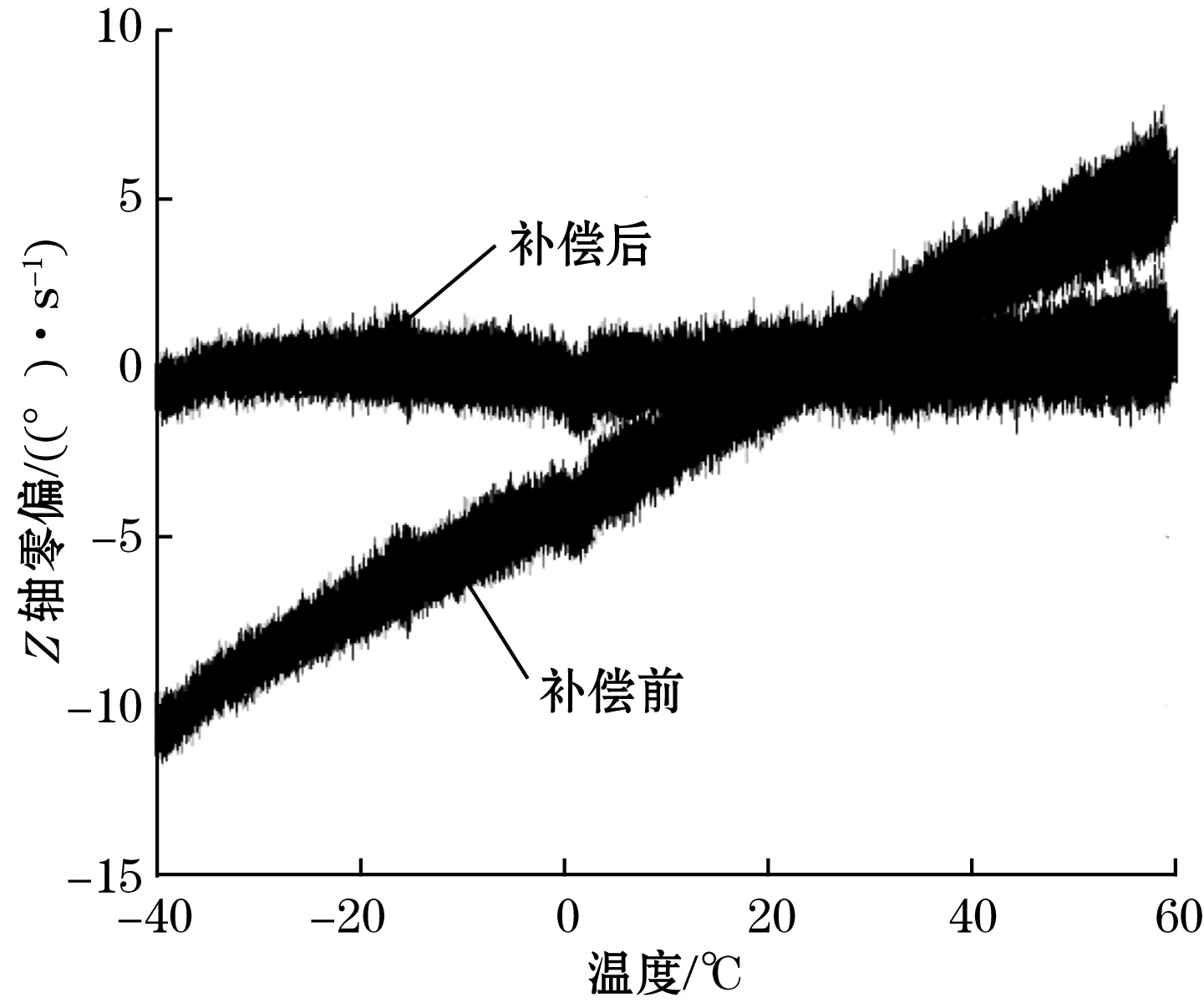
图8 Z轴零偏-温度的玻尔兹曼模型补偿效果
将基于零偏-温度的玻尔兹曼模型与线性模型补偿方法进行比较,比较结果见表2。

表2 玻尔兹曼模型与线性模型比较
由表2可看出,采用零偏-温度的线性模型和玻尔兹曼模型对金属壳谐振陀螺进行温度补偿后,陀螺的温度漂移得到了抑制,在-40~60 ℃的温度区间内的漂移标准差大幅降低,补偿效果明显。相比线性模型,玻尔兹曼模型具有更好的补偿效果,补偿后,陀螺漂移最大值降低到3.2 °/s以下,标准差降低了80%以上。
4 结束语
本文对金属壳谐振陀螺的温度误差机理进行分析,结合温度实验,建立金属壳谐振陀螺温度误差的线性模型和玻尔兹曼模型,并通过温度误差模型对陀螺输出零偏进行温度补偿。实验结果表明,基于玻尔兹曼模型的补偿效果优于线性模型的补偿效果,补偿后的陀螺输出精度显著提高,补偿效果明显。
