一道试题解法赏析

余永波

(云南省绥江县第一中学 657700)

一道好的试题总会留下很大的拓展空间,让你产生无尽的遐想,细细品来,让人回味无穷,因而成为学生学习数学的航标.命题者在命制试题时,都会对曾经出现过的“好题”密切关注, 这类“好题”涉及高中数学主干知识的每个角落,同时蕴藏着丰富的思想方法.

题目若正数a,b满足ab=a+b+3,则ab的取值范围是____.

从不同的角度、用不同的方法去解决同一个问题,要求考生善于观察与分析,紧扣条件和问题的结构特征,通过多种视角探寻解题方法,选择最优解法,从而提高解题能力和学习效率.

解法3 由题可知ab-3=a+b>0,即ab>3.而(a+b)2≥4ab,即(ab-3)2≥4ab.变形得(ab)2-10ab+9≥0,得ab≥9或ab≤1(舍).而ab>3,故ab≥9.

启迪与反思通过多种视角运用基本不等式及其变形公式巧妙地将“相等”关系转化为“不等”关系,是解此类问题的常规解法,变形过程中不可忽视变量的范围.上述几种解法中等号成立的条件都是a=b=3.

启迪与反思对分式型函数,可利用分离常数法和结构变换法,再结合函数单调性或基本不等式求函数最值.

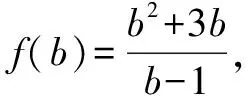
由于b+1>0和(b-1)2>0,所以当b>3时,f′(b)>0,即f(b)为增函数；当1

启迪与反思:导数法是求函数最值的一种普遍性很强的方法,但它未必是求最值的最优方法.

启迪与反思此法的精髓是方程思想,即通过换元,构造出一元二次方程,利用根与系数的关系将两个变量的问题转化成一个变量的问题.一般遇到“a+b”和“ab”,可将a、b视为一元二次方程的两根.

在高三复习过程中,同学们要牢固掌握基础知识,注重知识的渗透,灵活运用数学思想方法.对于 “好题”,要多咀嚼、要多回味、磨渗悟透,以求“一叶知秋”,以达“一雨普滋,千山秀色”之效.