追及与相遇问题的教学

孙云贵

(海南省海口市海南中学 571158)

追及和相遇问题，在高中物理的教学过程中，在学生看来，是学习中的难题，对教师来说，是教学中的难点.之所以有这种现象，我认为是因为是教师在教学中存在一些小问题.下面笔者结合自己的教学经验，谈一谈看法，跟同仁们商讨.

要做好追及和相遇问题的教学，教师在备课时，应有整体考虑，特别是《课程标准》中似乎是不太重要的物理概念，比如参考系、位置、时刻的概念，要讲透.这一点，往往被忽视，在教学中通常是一带而过，简单讲一下，这正是造成教学中对追及问题的把握感到非常困难的根本原因.

物理教学，要回归物理问题本身，才是解决问题的“捷径”.就这个问题来说，在教学过程中，首先要引导学生理解什么是“相遇”；其次，要引导学生学会怎样求“位置”；第三，比较在某同一时刻两物体的位置；第四，引导学生归纳出追及和相遇问题的典型模型及解决方法，数学处理技巧.

什么是相遇？所谓“相遇”，用物理语言来，就是某时刻两物体的位置相同.所谓“追上”，也是某时刻，一个本来在“后面”物体运动到本来位于“前面”的物体的位置.搞清楚了这一点，在教学中，我们就可以对症下药.

由于高一学生在学习追及和相遇的时候的知识储备，暂时只能解决物体在一条直线运动问题.在这个前提下，制定教学计划.

具体的教学步骤可分为以下几步.

第一步，引导学生学会根据具体问题选择合适的参考系，建立相应的坐标系.一般情况下，选“地面”为参照物，建立参考系，是一维坐标系，这样学生易于理解.

第二步，引导学生学会如何在坐标系如何表示物体的位置：坐标系中的坐标.

第三步，引导学生学会如何计算物体的位置.

物体在t时刻的(原)位置坐标为x0，自t时刻开始的Δt时间内的位移是s，则t+Δt时刻物体的(末)位置是x0+s.当然，要强调，位移是矢量，在一维坐标系的情况下可用代数形式表示.如图1所示.

图1

用矢量式表示即是：

r(t+Δt)=r(t)+s.

在一维情况下可表示为：

x(t+Δt)=x(t)+s

第四步，引导学生理解解题的步骤.弄清两物体的初始位置x10和x20；分别分析两物体的运动过程，求出题目中设定的条件下且在相同的时间段内运动的位移s1和s2；用“第三步”中的方法表示出两物体的末位置x1和x2；比较x1和x2，如果相遇(相等)则两位置相同(两物体相遇)，从而可列出方程；求解方程并解释结果的涵义.如果是求解“追不上”，则可列出不等式求解即可.

第五步，结果案例，展示解决问题的过程.

第六步，归纳总结追用与相遇问题的典型类型，特别是高一刚学过的典型的直线运动模型进行分析，能否追上及追上追不的判据.这一点，可以结合下表进行分析(教师只要分析部分做示范，可采用包括图象等各种手段进行分析，其余的可作为学生课作业).

追赶物体运动情况被追物体运动情况匀速运动匀加速运动匀减速运动匀速运动匀加速运动匀减速运动

案例分析示例

案例1 在高速公路上，有时会发生“追尾”的事故——后面的汽车撞上前面的汽车.请分析一下，造成“追尾”事故的原因有哪些？我国高速公路的最高车速限制为120 km.设某人驾车正以最高时速沿平直高速公路行驶，该车制动时产生的加速度大小为5 m/s2，司机的反应时间(从意识到应该制动至操作制动的时 间)为0.6 s - 0.7 s.请分析，应该如何计算行驶时的安全车距?

已知：v0=120 km/h，t1=0.7 s，a=-5 m/s2,求：smin=?

解以地面为参考系，乙车开始运动的方向为正方向，以发现甲车时刻为起始时刻，则

(1)在反应时间内，乙车的位移为s1=v0t1；

(2)制动开始到最后停止(假设不追尾)的位移

答：行车时安全距离至少为134.2 m.

图2

案例2 如图2所示，甲、乙两车沿着同一条平直公路同向行驶，甲车以速度20 m/s 做匀速运动，乙车原来速度为4 m/s，从距甲车128 m处以大小为1 m/s2的加速度做匀加速运动，问：乙车经多长时间能追上甲车？

分析画出两车运动的示意图如图3所示.

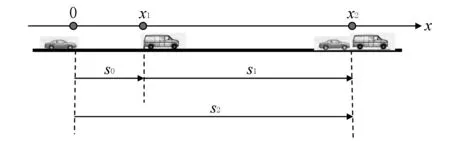
图3

分析两车运动的过程

为什么两车一定会相遇(追得上)？

两车运动的v-t图象如图4所示.可以分析出乙车一定能追上甲车！

假定经时间t，乙车追上甲车，只要求出两车在时间t内的位移就可以表示出它们t时刻的位置坐标，由于追上时位置坐标相同，可以以此为等量关系列方程，解出时间t.

图4

对甲，t时刻的位置：

x2=x1+s1=s0+v10t

对乙，t时刻的位置：

就得到关于t的方程：

解得：t= 38.624 s.

追及和相遇问题作为匀变直线运动规律的综合应用实例，表面上看，问题很复杂，在教学中很难把握，实际上，只要我们冷静思考，从物理学的“运动”本身出发，就可以较为方便地引导学生理清思路，从而解决问题.