六谈转化与化归

崔 文 侯宇虹

(1.山东省文登第一中学 264400;2.山东省文登南海高级中学 264400)

数学核心素养提升的主要表现是能够对复杂问题进行转化，化抽象为具体，复杂为简单.纵观高考题目，常见的转化方法有以下几种类型.

一、直接转化法

把原问题直接转化为基本定理、基本公式或基本图形问题.

例1 在△ABC中．sin2A≤sin2B+sin2C-sinBsinC,则A的取值范围是( ).

答案C

点评本题主要考查解三角形，突出“边角互化”这一转化思想的应用.

二、换元法

运用“换元”把较复杂的函数、方程、不等式问题转化为易于解决的基本问题.

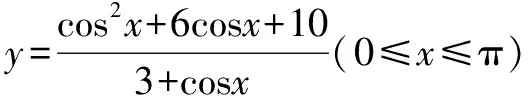
点评我们使用换元法时，要遵循有利于运算、有利于标准化的原则，换元后要注重新变量范围的选取，一定要使新变量范围对应于原变量的取值范围，不能缩小也不能扩大.

三、数形结合法

研究原问题中数量关系(解析式)与空间形式(图形)关系，通过互相变换获得转化途径.

例3 已知a，b是平面内两个互相垂直的单位向量，若向量c满足(a-c)·(b-c)=0，则|c|的最大值是( ).

答案C.

解析因为(a-c)·(b-c)=0，所以(a-c)⊥(b-c)．

点评通过“以形助数，以数解形”，使复杂问题简单化，抽象问题形象化，有助于把握数学问题的本质．

四、构造法

用构造法解题的关键是由条件和结论的特殊性构造出数学模型，从而简化推导与运算过程．

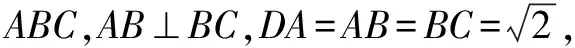
解析如图，以DA，AB，BC为棱长构造正方体，设正方体的外接球球O的半径为R，则正方体的体对角线长即为球O的直径，所以

点评本题巧妙地构造出正方体，而球的直径恰好为正方体的体对角线，问题很容易得到解决．

五、特殊化方法

把原问题的形式向特殊化形式转化，并证明特殊化后的问题，结论适合原问题.

点评有些题目看起来较为抽象，貌似不易解决，但结合具体数学情境，联系相知，建立模型，把一般问题特殊化，以启迪解题思路，寻找解决问题的突破口.

六、补集法(正难则反)

若问题从正面入手难以解决，可将问题的结果看作集合A，而把包含该问题的整体问题的结果类比为全集U，通过解决全集U及补集∪A获得原问题的解决.

解析g′(x)=3x2+(m+4)x-2.若g(x)在区间(t,3)上总为单调函数，则①g′(x)≥0在(t,3)上恒成立，或②g′(x)≤0在(t,3)上恒成立．(正反转化)

点评由于不为单调函数有多种情况，先求出其反面，体现“正难则反”的原则．一般地，题目若出现多种成立的情形，则不成立的情形相对很少，从后面考虑较简单，因此，间接法多用于含有“至多”、“至少”及否定性命题情形的问题中．

总之，转化与化归思想在高中数学中占有十分重要的地位，数学问题的解决，总离不开转化与化归，它即是一种数学思想又是一种数学能力，高考对这种思想方法的考查所占比重很大，是历年高考考查的重点.