高中数学解题中圆锥曲线参数方程的应用

何金建

(福建省泉州市奕聪中学 362015)

我们可以看到过去的教育还是主要针对学生的学科知识的记忆性学习，对学生的学科知识进行传授，更加关注的是学生的单一学习能力，而学生的自己的综合能力则没有更多的关注，在其他素质等的培养也是不那么关注，没有当作重点进行研究.而我们都知道，高中数学属于理科性质学科，本身具有一定的难度，数学是研究数字和事物变量等关系的一种具有很强的逻辑性的学科，但也是学生们比较难掌握的一门学科.这也是因为数学学科本身知识具有抽象性、应用性和逻辑性等.其中比较有代表性的就是高中数学中的圆锥曲线参数方程的应用了，这是一种相对比较难的用参数方程来解析圆锥曲线的类型题目，解题思路和解题计算能力都是要求比较高的，所以对圆锥曲线参数方程的解题分析可以为学生的学习成绩的提升做好充分的准备和基础.

一、创新思维：针对高中数学圆锥曲线方程应用中的解决最值的问题

当下，需要以学生为主，关注学生实际需求，学生的探索求知欲望的起点就是质疑，也是创造性和发散性思维形成的前提，这是提高学生数学学习能力的关键.

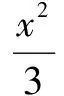
先观察题型可以发现此为椭圆题目，具体分析有：开始要结合椭圆基本知识写出椭圆的参数方程，再调动学生脑海中的点到直线的距离的三角关系式知识，从而就可以找到求距离的最小值的切入点了.

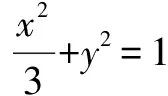
需要注意的是直线上的点坐标不容易直接使用，不可以达到解题的目的，所以需要考虑建立适当的曲线的参数方程，换个思考方式，及创新思维来解决问题.

二、探索性思维：针对焦点三角形的问题可以适用定义与正余弦定理

先观察本题可以发现这是一种需要有基本的知识储备，要对学习过的概念有所深刻了解和感悟，对正余弦知识很熟悉和可以灵活思考，同时理解面积公式才能更好地解答此题.

(2c)2=|PF1|2+|PF2|2-2|PF1|·|PF2||cosθ|②.

由圆锥曲线中的双曲线定义能够得到，

|PF1|-|PF2|=2a③.

三、学生的自主学习能力需要提升：采用圆锥曲线解决参数方程之范围问题

演算此题过程中，学生自我的思维模式不能求急，不能守旧，需要学生非常熟悉自己所学知识，以达到可以自我分析研究的程度，从而可以锻炼出学生的自主学习能力.学生有了更高的自主学习能力，在演算题目中的反复试验后还没有达到解题的目的时，就需要我们的老师来指导或者和学生交流来让学生得出最后的答案.这样的解题思路后还需要最后的总结.

解依题可知，M的坐标可以用(a，0)表示.假设N点坐标为(tcosθ，bsinθ)，同时，结合ON⊥MP可知：

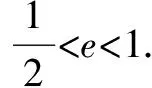
四、圆锥曲线参数方程应用中的注意问题

知识综合的运用能力在我们常见的高中数学问题中是非常必须的，尤其是在圆锥曲线参数方程应用问题中尤为突出，学生的运算思维和结构思考能力是必须的.因此，高中生的自身基础知识需要很熟悉，对圆锥曲线参数方程各种概念牢牢把握，再进行灵活运用，注重思考，从而更好并迅速掌握住高中数学题目的内涵而解题.