发射药颗粒间摩擦系数测定及其对装填密度的影响

2019-03-27郑向阳张领科符少波

弹道学报 2019年1期

郑向阳,张领科,符少波

(1.南京理工大学能源与动力工程学院,江苏南京210094;2.西安北方惠安化学工业有限公司,陕西西安710300)

火炮的内弹道设计是整个武器系统设计的核心,设计的目标是确定满足指标的装填条件和膛内构造参数等。为了提高发射药装填密度,通常将粒状发射药表面用石墨处理增加光滑度[1]。因此,摩擦系数的测定对研究发射药颗粒间摩擦系数对装填密度的影响具有重要的意义。滑动摩擦的研究和理论较为成熟,对于滚动摩擦的研究和测量相对较少,如何测定滚动摩擦系数是核心和重点[2]。

在颗粒摩擦系数研究中,离散单元法发挥了越来越重要的作用。Zhao等[3]通过离散单元法探讨了滑动摩擦系数及滚动摩擦系数对堆积形成的影响,发现颗粒堆的形态是由滑动摩擦和滚动摩擦共同决定的;Nakashima等[4]得出颗粒的滚动摩擦系数对沙堆堆积角起决定作用,两者近似呈线性关系,受重力和颗粒半径影响很小;Ai等[5]对比了各种滚动阻力模型下模拟的沙堆堆积模型,认为传统的离散单元法将法向和切向的颗粒接触简化为阻尼和弹簧组合模型,对沙堆测量具有适用性;Ann-Sofie等[6]通过点源法模拟颗粒的堆积过程,得出颗粒间的滑动和滚动摩擦系数会对颗粒的流动性和堆积角产生较大影响;李贝等[7]提出一种滚动摩擦系数工程化测量方法,并通过对比实际堆积角与模拟堆积角,验证了测量的准确性。

本文以表面涂有石墨的发射药颗粒为研究对象,采用传统的斜面仪来测量发射药间的静摩擦系数。对于滚动摩擦系数的测定,基于离散单元法,模拟了一种点源式的堆积过程,获得模拟堆积角与滚动摩擦系数间的线性拟合方程,并基于实验堆积角进行参数标定来确定滚动摩擦系数,最后通过二次模拟来验证所测参数的准确性。

1 静摩擦系数的测定

1.1 实验原理

静摩擦系数测量原理如图1所示,A为可调节角度的斜面仪,为了测量物体B与A接触面间的静摩擦系数μs,将物体B放置在A的斜面上,调节斜面的角度,当B刚好处于将要滑动的状态时,记斜面与水平面间的夹角为α,则

式中:W为物体B所受的重力。

图1 静摩擦系数测量原理图

1.2 实验方法

本实验采用如图2(a)所示的斜面仪测量发射药颗粒间的静摩擦系数。该装置包括:可调节支架、平板、双面贴和发射药颗粒。首先,将双面贴粘贴在平板上,再选取圆柱形发射药紧凑排列地粘贴在双面贴上,如图2(b)所示,再将平板放置在可调节支架上,通过可调节支架来调整平板的倾斜角,最后随机选取几粒梅花形发射药放置在排列的圆柱形发射药上(圆柱形与梅花形发射药表面均为石墨材料,实验表明它们的静摩擦系数近似相等),改变可调节支架的倾角使发射药刚好处于有滑动趋势的状态,再用量角仪测量此时斜面仪的夹角。

图2 静摩擦系数测量实验图

进行多次实验测量并取平均值,得出斜面倾斜角为9°～9.5°,从而可得发射药颗粒间静摩擦系数μs为0.158～0.167。

2 滚动摩擦系数的测定

目前,对非圆颗粒滚动摩擦系数的测定还没有准确成熟的测量方法,当颗粒的某参数未知时,参数标定的方法是一种有效便捷的研究手段,当模拟过程中调节或拟合出的颗粒参数值符合实验结果时,可认为该值为颗粒参数值。

文献[8-9]通过改变斜面倾角测量出椭球形糙米颗粒的静摩擦系数,基于离散单元法模拟颗粒堆积过程,得出模拟堆积角与动摩擦系数的线性关系,再运用实验所测堆积角进行参数标定;王云霞等[10]通过设计2种不同的玉米颗粒堆积实验,分别测出堆积角,再经过离散元模拟后得出2种实验各自的模拟堆积角与静摩擦系数和滚动摩擦系数的二元回归方程,将实验所测堆积角分别代入各自方程,联立计算出静摩擦系数与滚动摩擦系数。

本文基于上述学者的研究,采用离散单元法[11]模拟发射药颗粒的堆积过程,测定发射药颗粒间的滚动摩擦系数。步骤如下:进行发射药颗粒堆积实验,建立发射药颗粒离散元模型,确定颗粒接触模型,进行离散元模拟和参数标定,二次模拟验证。

2.1 发射药颗粒堆积实验

设计了一种点源式的颗粒堆积实验,实验原理如图3所示。

图3 颗粒堆积实验原理示意图

在平台上方固定一漏斗,漏斗下口离地面约9 cm,在漏斗上口处倾倒发射药颗粒,发射药选用14/19梅花发射药,颗粒在重力的作用下做自由落体运动,从漏斗下口处流出,逐渐在平台上形成颗粒堆,然后测量颗粒堆的堆积角。为了排除发射药颗粒与平台之间的摩擦对颗粒堆形态产生的影响,事先在平台上铺满了一层发射药颗粒,这样,颗粒的堆积可视为只有颗粒之间产生了堆积摩擦。形成的颗粒堆如图4所示。

图4 实验颗粒堆

在测量颗粒堆堆积角时采用GetData图像处理获得边界轮廓线,并获取拟合方程,得到方程的斜率k,如图5所示,图中,x,y为图像的像素点。

图5 边界轮廓图像处理

令堆积角为θ,则

(1)

处理后得到的实验堆积角θ=23.46°。

2.2 发射药颗粒离散元模型

本文以实验中的14/19梅花发射药颗粒为研究对象,模拟所需的发射药物性参数来自参考文献[12],如表1所示,药型参数数据由工厂提供,如表2所示,表中,ν为发射药泊松比;ρ为发射药密度;G为发射药剪切模量;μs为发射药间静摩擦系数;e为发射药间恢复系数;d0,e2,2c分别为发射药孔径、弧厚和长度。

表1 模拟所需材料物性参数

表2 14/19梅花发射药药型参数

EDEM为目前功能最强大、应用最广泛的离散元建模模拟软件[13],可导入SolidWorks所建立的发射药三维模型,以此为颗粒模板建立发射药离散元模型。根据表2药型参数建立的SolidWorks三维模型如图6所示,离散元模型如图7所示。

图6 14/19梅花发射药三维模型

图7 14/19梅花发射药离散元模型

目前EDEM通过选用多个球形颗粒填充颗粒模板的方式来建立颗粒离散元模型,因此所建立的离散元模型与颗粒模板存在一定的差异,但颗粒模板对离散元模型的建立起着重要的约束和规划作用。

2.3 颗粒接触模型与离散单元法

发射药颗粒模型视为软球模型[11],即模拟颗粒间的碰撞过程时,视碰撞发生在一小段时间范围内,半径分别为R1和R2的颗粒发生了接触碰撞,颗粒间碰撞面产生的法向重叠量为δn,接触半径为Ra,如图8所示。再由接触模型公式计算得到接触力F和接触力矩T,即力-位移关系。

图8 软球模型

发射药颗粒视为非粘连颗粒,基于以上假设,颗粒的接触模型采用Hertz-Mindlin无滑动接触模型[14-15],如图9所示。该模型将颗粒间在接触点的碰撞分解到法向和切向2个方向,接触力简化为弹簧和阻尼器的并联,Kn和Kt分别为法向和切向弹性系数,dn和dt分别为法向和切向的阻尼系数。

图9 接触力学模型

颗粒在堆积过程中主要受自身重力mig,颗粒间法向、切向碰撞接触力Fn,Ft,法向、切向阻尼力Fn,d,Ft,d,还受切向力造成的力矩和滚动摩擦力矩Tt和Tr,根据牛顿第二定律,得到颗粒的运动方程:

(2)

在上述力和力矩的作用下颗粒发生移动和滚动,在运动过程中颗粒所受到的力和力矩[13]如下。

法向接触力:

式中:E*为等效弹性模量;Ei,Ej分别为颗粒i,j的弹性模量;νi,νj分别为颗粒i,j的泊松比;R*为等效颗粒半径;Ri,Rj分别为颗粒i,j的半径。

法向阻尼力:

式中:

式中:β为与恢复系数e相关的参数,kn为法向弹性系数,m*为等效质量,vn,rel为法向相对速度。

切向接触力:

Ft=-ktδt

式中:

式中:kt为切向弹性系数,δt为切向重叠量,G*为等效剪切模量。

南水北调中线工程渠漳古段SG3标道桩号74+660至75+095段属于I型（轻微）—II（中等）级湿陷性黄土场地。该段渠道筑堤工程早已完成施工，后发现该段黄土地基具有湿陷性，不仅在南水北调工程中具有代表性，在其他水利工程中特别是处理旧有渠道地基问题上也具有广泛的代表性。由于该段属于筑堤完成后发现黄土的湿陷性，且该段筑堤高度在原地面以上均超过了6m，选择方案时面临着巨大的土方工程量增加的困难，加之南水北调中线工程工期和工地周边土源紧张导致外购土困难，给解决该地基问题带来了诸多制约因素。

切向阻尼力:

式中:vt,rel为切向相对速度。

力矩:

Tt=Ri×(Ft+Ft,d)
Tr=-μrFnRiωi

式中:μr为滚动摩擦系数,Ri为颗粒半径,ωi为颗粒在接触点处的单位角速度向量。

利用中心差分对式(2)进行数值积分得到颗粒的更新速度:

(3)

式中:Δt为时间步长。

对式(3)进行积分得到时间步长结束时的位移:

(4)

由此得到颗粒新的位移值,将该位移值代入力-位移关系中便可计算颗粒所受新的作用力。基于牛顿第二定律,新的作用力便用于求解下一时间步长颗粒新的位移值,如此进行循环计算,便可实现对颗粒运动的跟踪,这便是离散单元法的基本求解过程,如图10所示。

图10 离散单元法计算循环

2.4 离散元模拟与参数标定

模拟方法和过程与实验应尽量保证一致,如图11所示,漏斗上口处为在EDEM中创建的颗粒工厂[13],用于生成发射药颗粒的离散元模型。将颗粒工厂设置为生成位置随机的14/19梅花发射药颗粒,颗粒在重力的作用下做自由落体运动,最终落在地面上,逐渐形成颗粒堆。在模拟中所建立的漏斗模型与图3中实验所用的漏斗形状尺寸完全相同。实验中所倾倒的发射药总质量为2 kg,14/19梅花发射药单个颗粒质量约为1.36 g,因此,颗粒工厂大约生成1 500个颗粒。

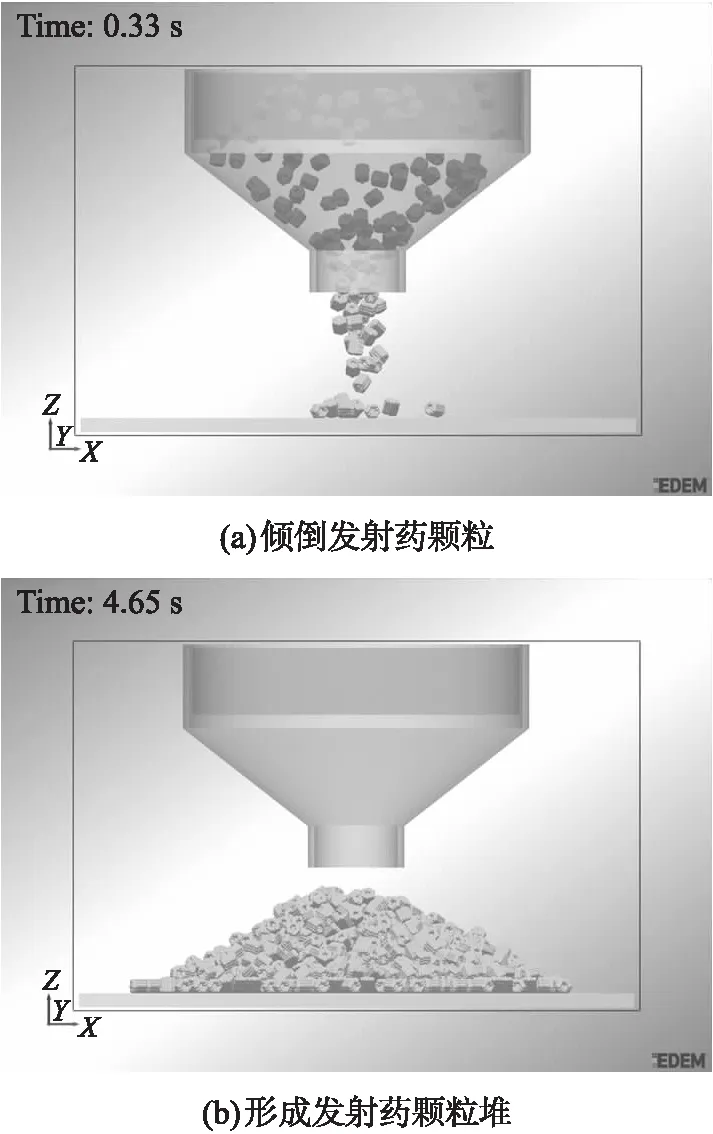
图11 模拟过程

为了分析滚动摩擦系数μr对模拟堆积角θ的影响,μr分别取0.04,0.06,0.08,0.10,其余参数取值均相同;静摩擦系数μs取实验测量值0.16。通过模拟获得不同μr对应的模拟颗粒堆,如图12所示。

图12 不同μr的模拟颗粒堆

对图12(a)～12(d)的颗粒堆进行边界轮廓图像处理,获取模拟堆积角。为了提高模拟堆积角测量的精度,对颗粒堆4个方向(x,y轴正、负方向)的边界轮廓进行图像处理再取其斜率|k|的均值,结果如表3所示。

表3 斜率拟合结果

表3中μr对应的模拟堆积角θ分别为21.8°,22.7°,23.8°,24.6°,可见随着颗粒滚动摩擦系数的增大,颗粒堆的堆积角近似呈线性增大趋势,比较符合Nakashima的研究结果。将μr与θ的值进行线性拟合得到拟合方程:

θ=47.5μr+19.9

(5)

实验中所测堆积角θ=23.46°,将其代入到式(5)中,得到滚动摩擦系数μr=0.076。

2.5 二次拟合

为了对该标定值进行验证,取发射药颗粒的滚动摩擦系数μr=0.076,其他参数取值不变,进行堆积过程的二次模拟,结果如图13所示,由图13可得模拟颗粒堆与图4实验颗粒堆的形态十分相似。

图13 二次模拟颗粒堆

为了对比结果的相似程度,对图13颗粒堆的边界轮廓进行图像处理,得到的模拟堆积角约为23.61°,接近实验值23.46°,说明参数标定法测量滚动摩擦系数可行,同时也是一种有效便捷的研究手段。

3 模块装填模拟

为了探究发射药颗粒间摩擦系数对装填密度的影响,将摩擦系数取不同值,对口径为122 mm的模块进行发射药装填模拟。模块装药为目前大口径火炮装药技术的发展方向,装填密度的计算主要基于每个模块的装药量,而模块的装药量主要取决于模块形状、发射药的药形、摩擦系数和装填状态等。因此,运用EDEM进行装填过程的模拟,应保证除摩擦系数外的其他因素相同,装填状态初步设为自然装填,未发生振动。此外,还需建立模块的几何模型,模块为圆柱形容器,经实验测量,口径为122 mm,高度为150 mm,如图14所示。

图14 口径为122 mm的模块

建立的模块几何模型如图15所示,模型上方的圆柱形区域为颗粒工厂,用于生成发射药颗粒的离散元模型。生成的颗粒模型在重力的作用下做自由落体运动,最终落到模块容器中,直至装满模块,以此来模拟自然装填过程。最后根据装满模块所需生成发射药颗粒的数量及单颗发射药颗粒的质量,来近似计算模块的装药量和装填密度。

颗粒工厂生成的是14/19梅花发射药模型。模拟时将发射药颗粒间静摩擦系数μs取实验测量值0.16,滚动摩擦系数μr取标定值0.076。当发射药装满模块时,模拟结果如图16所示,大约需要1 220个颗粒,经实验测量得到的单颗平均质量约为1.36 g,可得此时的装药量约为1.660 kg。

图15 模块几何模型及模拟过程

图16 装满发射药的模块

为了探究摩擦系数对装填密度的影响,改变μs与μr的值,其他模拟条件不变,模拟模块装满发射药所需的颗粒数(装药量)。实验中所选取的发射药颗粒表面已涂有石墨材料,比较光滑,因此可将μs与μr的值调大,来模拟颗粒表面比较粗糙时(可视为未涂有石墨材料)的情况。

先将μs的值调大,取模拟值0.4,μr的值不变,重复模拟过程。考虑到若生成原有颗粒数1 220时可能产生较多的颗粒溢出,因此设置颗粒工厂先生成1 155个颗粒,观察模拟结果,如图17所示。

图17 μs调大后的模拟结果

可见,当μs的值调大后,虽然生成的颗粒数比之前少了,但发射药依然装满了模块,甚至略有溢出。

再将μr的值调大,取模拟值0.2,μs不变,取模拟值为0.4,当同样生成1 155个颗粒时,观察模拟结果,如图18所示。

可见,当μr的值调大后,同样生成1 155个颗粒时,模块所装发射药的状态较之前显得更加饱满,且有部分颗粒溢出。

图18 μr调大后的模拟结果

在发射药自然装填模块的模拟中,可以观察到,通过改变μs与μr的值,模块装满发射药的模拟结果产生了较大的差异。颗粒间的摩擦系数较小时,模块可以装更多的发射药颗粒,即装药量和装填密度比较大;当摩擦系数调大后,由于颗粒表面的粗糙程度加大,模块的装药量也随之产生了明显的下降,这说明摩擦系数对装填密度的影响是一个不可忽略的因素。