低压长脉冲作用下PBX炸药的响应特性
2019-03-27孙文旭王万军罗智恒代晓淦章定国
孙文旭,王万军,罗智恒,4,代晓淦,刘 彤,章定国
(1.南京理工大学 理学院,江苏 南京 210094;2.中国工程物理研究院 化工材料研究所,四川 绵阳 621900;3.中国工程物理研究院 成都科学技术发展中心,四川 成都 610200;4.中国工程物理研究院 研究生院,四川 绵阳 621999)
关于含能材料冲击起爆国内外已做了大量的研究,多数集中在高压和高加载率研究领域,也就是一般所说的冲击转爆轰(SDT)。然而,含能材料会经受各种低于SDT的加载条件,并且同样会发生强烈的反应[1-2]。如高速侵彻战斗部在对混凝土等目标进行侵彻时,炸药受到压力较低而作用时间长达数百到上千微秒的低压长脉冲作用。一方面,低冲击下炸药延迟起爆(XDT)现象本身的机制尚不清楚;另一方面,低幅值压力作用过程涉及到多种因素的相互影响,具有较大的不确定性,因此深入认识低压长脉冲作用下PBX炸药的力学响应特性尤为困难[3-5]。
本文开展实验室级别的低压长脉冲点火试验研究,通过测试低压长脉冲撞击作用下炸药的动态力学响应,获得被撞击炸药的动态应力、应变参数,分析其与撞击脉宽、撞击压力的关联,获得一种典型的浇注PBX-1炸药在低压长脉冲撞击作用下的力学响应及反应规律。采用LS-DYNA非线性有限元软件对落锤冲击载荷作用下炸药内部压力变化过程进行数值模拟,对比峰值应力、应力上升时间等主要力学参数,结果与试验测试结果具有较高的吻合度,可以很好地模拟炸药在低压长脉冲冲击下的力学响应特性。
1 大落锤试验原理
根据应力波理论可知,当硬材料撞击软材料时,在不考虑卸载波影响的前提下,硬材料会持续对软材料进行加载,直至硬材料速度降为0,相应的应力幅值逐渐降低。通过控制加载条件,可以使应力幅值缓慢衰减,如采用高阻抗硬材料。根据上述分析,本文利用大质量钢质落锤撞击放置在基座上的样品,在样品中实现低压长脉冲加载,大落锤加载试验示意图如图1所示。

图1 大落锤加载试验示意图
基于X-t波系图,对大落锤撞击下样品内部应力波的传播和反射过程进行分析,如图2所示。当大落锤撞击样品时,在落锤和样品的撞击面上产生压缩加载波并同时向落锤和样品内部传播。大落锤中的加载波经过自由面的反射作用应力卸载到0,并向样品方向传播一个卸载波,经过加载和卸载,大落锤的速度有所降低。在样品中的加载波与刚性固壁作用后,会反射一个加载波。该加载波又会再次与大落锤作用,由于大落锤具有高阻抗特性,又会向样品中反射一个加载波。由此在大落锤中卸载波达到撞击界面之前,样品要经历多次加载波的压缩作用,应力不断上升,同时在大落锤中也形成一系列加载幅值较小的扰动加载波。这一系列扰动加载波经过自由面的反射,同样会反射一系列的扰动卸载波,但由于幅值较小,不会对大落锤速度造成明显影响。当大落锤的卸载波达到撞击界面时,大落锤对样品产生二次加载。由于大落锤速度有所降低,样品中的应力幅值也会有所下降。由于二次加载产生的应力波在大落锤与固壁之间来回反射,样品中应力与第一个周期一样,也会不断增加[6-10]。
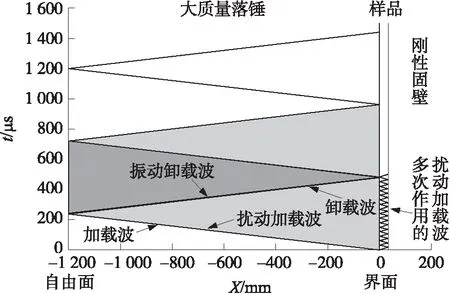
图2 大落锤撞击基座上样品的应力波作用波系
2 试验研究
采用尺寸为φ40 mm×30 mm的柱形PBX炸药,其组分为HMX/Al/HTPB,配比为60∶35∶5。样品放置在厚度为8 mm的钢中进行约束,总体尺寸为φ56 mm×46 mm,在壳体上表面选用3 mm厚的聚四氟乙烯用于对应力脉冲的整形,如图3所示。试验中,在样品与上、下表面的整形器之间各放置了一个薄膜式的PVDF用于测量样品的轴向应力。在壳壁表面粘结了环向和轴向应变片,用于测量壳体的变形;利用高速相机通过限位装置上的开孔对带壳炸药变形以及可能的反应发光现象进行了拍摄。
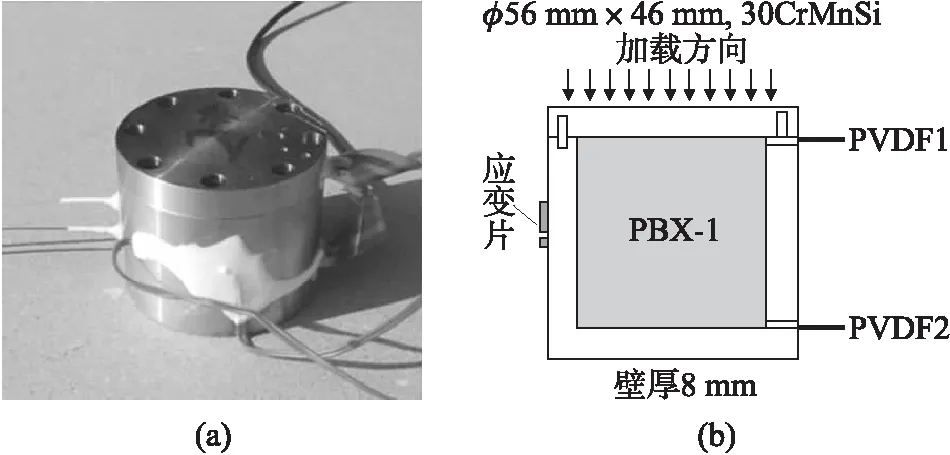
图3 带壳炸药试验装置及测试布局
第1发试验中,大落锤的实测撞击速度为3 m/s,高速摄影给出了带壳炸药在大落锤撞击下的响应过程,如图4所示。大落锤撞击后,先造成聚四氟乙烯缓冲层的墩粗变形,并对带壳炸药进行加载。在600 μs时,聚四氟乙烯缓冲层在较大变形下出现断裂破坏,在1 200 μs时,大部分聚四氟乙烯缓冲层碎裂分散,由此造成带壳炸药的短时卸载,随后大落锤进一步加载,带壳炸药继续变形,直至与限位装置发生相互作用。

图4 第1发试验撞击过程高速摄影结果
通过应力和应变波形,可以获得大落锤撞击过程的量化信息,如图5所示,图中,ε为应变,σ为应力。在大落锤加载下,炸药上表面的轴向应力逐渐增加,在撞击后300 μs时可观测到局部卸载现象,此后应力继续增加;800 μs左右达到峰值,上表面的轴向应力峰值约为100 MPa,下表面约为40 MPa;在900 μs时聚四氟乙烯大面积破碎飞散,造成撞击过程中更为严重的卸载现象;整个加载过程的持续时间约为1.5 ms。在应变测量结果中,环向受拉伸作用产生变形,最大应变为0.013;轴向受压缩作用产生变形,最大应变为0.014;整个带壳炸药呈墩粗形状。此外,在应变波形中,也可以在对应时刻观测到缓冲层的破碎飞散过程对壳体环向和轴向应变波形的影响。同时由图6中的回收样品可知,在较低的撞击速度下,壳体变形处于弹性范围,当完全卸载后,壳体恢复原有形状,回收的带壳炸药试样没有变形。

图5 第1发试验炸药试样的应力、应变波形

图6 回收的带壳炸药试样
第2发试验通过增加落高将撞击速度提升至5 m/s,其余试验条件和第1发试验保持一致。高速摄影给出了带壳炸药的响应过程,如图7所示。大落锤撞击后,带壳炸药出现墩粗变形,在撞击后1 000 μs时可观测到壳壁直径方向明显的尺寸变化;1 800 μs时,限位装置内壁出现反射发光现象,这是内部装药反应引起的,随后发光进一步增强,直至熄灭。

图7 第2发试验撞击过程高速摄影照片
图8给出了炸药反应情况下测得的应力和应变波形。由图可知,在撞击后900 μs时样品的轴向应力和壳体应变达到最大值,应力的峰值约为220 MPa,环向和轴向的最大应变约为0.045。
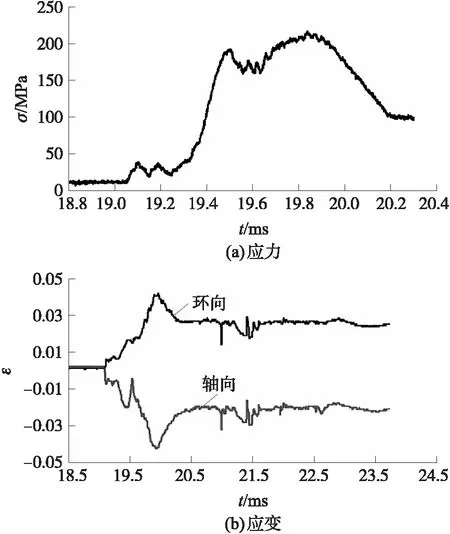
图8 第2发试样应力及应变波形
3 动力学有限元数值模拟
3.1 数值仿真模型
采用LS-DYNA非线性动力学计算软件,对不同速度的大落锤撞击下壳体的变形过程以及炸药的化学反应过程进行数值模拟。根据物理过程的轴对称特性,采用二维轴对称方法建立计算模型,如图9所示。基本单位选取为cm-g-μs,其余物理量的单位根据基本单位制导出。计算网格均采用Lagrange网格,壳体底部通过施加边界条件约束其法向位移。

图9 1/2轴对称有限元计算模型
采用Lee-Tarver点火增长模型描述PBX炸药在撞击作用下的化学反应速率。虽然点火增长模型通常用于描述炸药在冲击起爆过程中的化学反应速率,而大落锤低速撞击产生的压力脉冲与通常意义上的冲击波作用相比具有明显更低的峰值压力和更长的作用时间,但是,考虑到无论是低压长脉冲还是高压短脉冲作用下的炸药爆轰(爆燃或燃烧),其本质上都是压力诱导炸药发生快速的化学反应,而Lee-Tarvar点火增长模型中多参数能够保证其适用于各种压力诱导下的化学反应速率描述。本文采用三项式Lee-Tarver点火增长模型描述炸药在大落锤撞击下的化学反应过程:

(1)
式中:p为压力;F为反应度;t为时间;I为点火项系数;b为点火反应项指数;a为临界压缩度;x为压缩项指数;G1,G2为增长项系数;c,d,e,g为增长反应项指数;y,z为压力项指数。
与两项式Lee-Tarver模型相比,主要的不同在于将增长项分为两项:当热点作用仍然显著时,只发生类似于颗粒燃烧中出现的相对较慢的化学反应;当热点开始湮灭时,剩余的未反应炸药开始快速分解,能够用压力相关的增长速率进行描述。
PBX-1炸药的点火增长模型参数如表1所示,具体选用AUTODYN材料库中密度与PBX-1接近的PBX炸药冲击起爆模型参数。

表1 PBX炸药点火增长模型参数(20 ℃)
3.2 计算结果及分析
3.2.1 炸药内部压力变化规律
首先对炸药内部不同位置处的压力随时间变化历程进行分析,提取了炸药内部中心轴线上3个不同位置(见图9)的压力-时间变化曲线,如图10所示。通过对比不同撞击速度下的炸药内部压力变化历程可以看出,当撞击速度为3 m/s时,炸药内部的压力不超过30 MPa,而且压力随时间的推移而逐渐缓慢减小,因此没有发生明显的化学反应过程。当撞击速度增大至5 m/s时,3个观测点处的压力几乎同时在650 μs时开始上升,并在大约1 100 μs后上升至最大值300 MPa左右,然后压力再次减小至170 MPa。通过与图8中试验所得压力随时间变化规律的对比可知,数值计算中获得的压力随时间先增大后减小的变化趋势与试验结果基本一致,只是峰值压力大于试验测试结果,这也初步表明Lee-Tarver点火增长模型能够应用于炸药在低压长脉冲作用下的化学反应速率描述。
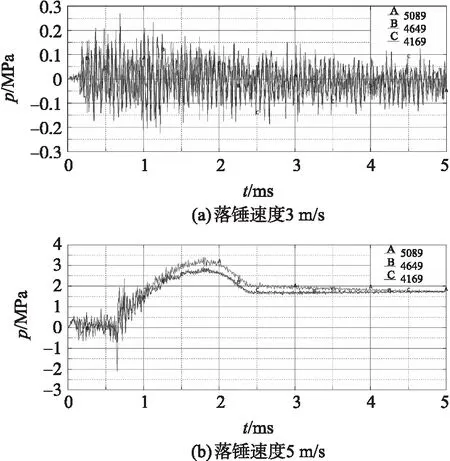
图10 不同撞击速度下炸药内部不同观测点处的压力-时间曲线
通过对图10(b)中的压力-时间变化曲线分析可以看出,低压长脉冲下的炸药化学反应与冲击起爆过程显著不同。在低压长脉冲作用下,不同观测点处的压力基本上同步变化,呈现出比较明显的整体特征。也就是说,在低压长脉冲刺激作用下,炸药内部各个位置在落锤撞击作用下处于基本相同的压缩状态,到达某一临界值后同时开始发生化学反应,而不存在明显的爆轰波传播过程。当撞击速度为5 m/s时,其峰值压力显著大于撞击速度为3 m/s时的峰值压力,表明炸药内部发生了明显的化学反应,这与高速摄影观测结果吻合。同时,装药壳体在内部高压作用下开始膨胀并发生塑性变形,壳体的塑性变形消耗掉一部分的炸药内能使其压力有所降低,化学反应减缓并最终停止,最终壳体内部压力保持不变。
3.2.2 壳体变形规律
为了定量观测装药壳体,本文在数值模拟过程中同时观测了不同撞击速度下壳体中心部位的轴向应变和径向位移,以撞击速度5 m/s为例,其轴向应变和径向位移如图11所示。从图中可以看出,数值模拟所得的轴向应变与图8中试验所得的轴向应变的变化趋势基本一致,计算所得最大轴向应变约为0.049,略大于试验测试结果0.045;最大径向位移约为0.142 cm,计算可得其对应的最大环向应变为0.05,同样略大于试验测试所得的0.045,这是由于数值模拟过程中化学反应速率相较试验过程较快,导致壳体内部压力大于实际情况。
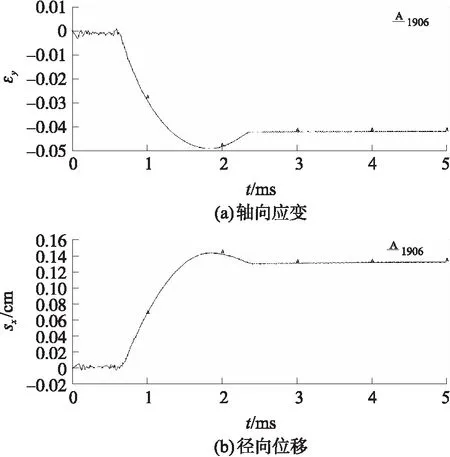
图11 撞击速度5 m/s的壳体变形情况
试验结果和数值模拟结果均表明,炸药发生明显的化学反应后,壳体将产生明显的塑性变形,壳体塑性变形的程度与炸药反应释放的能量呈正相关的关系。因此,本文的研究结果表明,可以采用壳体的塑性变形量作为衡量炸药在低压长脉冲刺激下反应程度的重要指标。
4 结论
①本文试验结果表明,通过大质量落锤低速撞击小面积样品进行轴向压缩,试验中应力幅值达到102MPa量级,脉冲持续时间大于1.5 ms,可用于炸药低压长脉冲点火研究;
②Lee-Tarver三项式点火增长模型可以较好地描述PBX-1炸药在落锤冲击下的化学反应过程,验证了该模型用于低压长脉冲作用下炸药点火特性分析的可行性;
③通过数值计算结果可知,随着落锤撞击速度的增加,炸药反应程度加剧,这与试验测试结果基本一致,炸药的反应程度可以用壳体的塑性变形量进行表征。
