斜激波与反应性气体界面作用的数值模拟

2019-03-27胡明媛陈耀慧栗保明

弹道学报 2019年1期

胡明媛,董刚,陈耀慧,栗保明

(南京理工大学瞬态物理国家重点实验室,江苏南京 210094)

高超声速发射器主要包括冲压加速器、电磁轨道炮以及二级轻气炮,其研究工作一直受到世界各国的关注。冲压加速器(ram accelerator)由美国华盛顿大学的Hertzberg教授在20世纪80年代提出[1],其工作原理与冲压发动机类似,即,在加速管中充入预混推进剂气体(氢气、氧气或甲烷、氧气),与冲压发动机中心锥形状相似的弹丸被初级炮以一定的速度射入加速管,控制预混气体在弹丸的中后部燃烧或者爆轰,产生的高压推动弹丸进一步加速[2]。理论上,冲压加速器可将弹丸加速至7～9 km/s[3]。由于冲压加速器具有显著的应用前景和潜在的军事价值,其研究受到了许多国家的重视,并开展了大量的实验、理论和数值模拟研究工作[4],其中包括对影响冲压加速器性能的各种因素,如弹丸材料和形状、加速管的装填压力、长度、几何形状以及混合推进剂的组成和配比等的研究。但到目前为止,冲压加速在实验室里实现的弹丸最高速度仅有2.7 km/s,管内马赫数为2.5～8.5[5]。冲压加速器弹丸发射速度限制机制是所谓的“注定推进剂分数”(doomed propellant fraction),指的是在足够高的马赫数下,弹丸头部弓形激波会在弹丸喉部或之前点燃推进剂,产生不启动(unstart)现象[6]。为了解决这种不启动现象,华盛顿大学的Higgins[7]提出了一种新概念挡板冲压加速器(baffled-tube ram accelerator),Knowlen等[8]对这种新型冲压加速器进行了数值模拟和实验研究,但并未给出弹丸的出口速度。

为了解决这种不启动现象,本文提出一种分层充气的概念,将冲压加速管进行内外分层,外层充入可燃预混气体,内层充入轻质气。这种分层充气的好处是:当弹丸在足够高的马赫数下运行时,气体经过头部的弓形激波的加热,温度达到了点火温度,但由于轻质气内没有氧化剂的存在,所以无法点火;而外层的可燃预混气经过激波压缩后可以被点燃或引爆,从而解决不启动现象。为验证这一方法的可行性,本研究根据以上思想,采用弹丸诱导的斜激波与可燃预混气和轻质气形成的气体界面相互作用的方式,用数值模拟的方法研究了冲压加速管正常启动和燃烧的问题。讨论了气体分层比例(预混气体充填量)和弹丸速度(来流速度)对气体混合及点火燃烧的影响。

1 数理模型

1.1 控制方程

考虑到研究的问题中较高的来流速度,可忽略流场中的黏性等分子输运特性,故可以采用二维带化学反应的多组分欧拉方程进行数值模拟:

(1)

式中:守恒量U、守恒通量G、H及源项S可分别表示为

U=(ρ1…ρKρuρvE)T

(2)

G=(ρ1u…ρKuρu2+pρuvu(p+E))T

(3)

H=(ρ1v…ρKvρuvρv2+pv(p+E))T

(4)

(5)

本文使用了课题组自行开发的计算程序开展计算,该程序已在可压缩反应流的数值模拟中得到了广泛应用[10-11],对于式(1)中G和H的空间微分形式,程序采用了全局Lax-Friedrichs矢通量分裂格式并结合九阶WENO格式[12]进行求解,这种高精度的格式能够精确地捕捉流场中的强间断和接触间断,同时能够有效避免计算结果的非物理振荡和流场的数值耗散;式(1)中的化学反应源项则采用隐式VODE软件包[13]进行求解。此外,本文采用了三阶Runge-Kutta方法来离散式(1)中的时间导数项,根据Courant-Friedrichs-Lewy(CFL)稳定性判据(CFL数小于1),本文取CFL数为0.5倍计算时间步长,以保证时间推进的数值稳定性。

1.2 计算模型

考虑一头部锥角为2δ的弹丸以初速u0自右端射入充有预混气体的管内,在管内靠近壁面一侧充有可燃预混气,而远离壁面一侧充有轻质气体,弹丸在轻质气中运动。当弹丸以超高声速运动时,会在头部形成斜激波,斜激波能够穿越可燃预混气和轻质气体形成的界面,从而与界面发生相互作用。界面在激波的作用下可以产生Richtmyer-Meshkov(RM)不稳定,同时波后界面两侧的气体的速度差还会导致Kelvin-Helmholtz(KH)不稳定,这些不稳定现象能促进预混气的着火进而形成爆轰,从而提供推力进一步加速弹丸的飞行。为简化问题,本文采用了图1所示的计算构型来研究斜激波与气体界面的相互作用过程。

图1 计算模型示意图

图1使用了以弹丸为参考系的Lx×Ly=0.48 m×0.1 m的矩形区域,图中,l1为轻质气厚度,l2为可燃预混气厚度。2种气体以速度u0由左侧进入计算域,弹丸形成的斜激波与2种气体的界面相互作用后,两者均会发生偏转。在初始条件下,令弹丸诱导的斜激波角度为β1,则斜激波与界面作用后的角度为β2。另一方面,波前水平的气体界面与激波作用后随气流方向的偏转而偏转,其偏转角为δ(弹丸半锥角)。由于弹丸锥角不变,所以波后气流偏转角也不变。初始时刻,给定波前气体的初始温度T0=298.15 K和初始压力p0=2.0 MPa,令气流偏转角δ=30°,则在给定入口速度u0的条件下,根据激波关系式[14]可以得出斜激波角度(β1和β2)及波后的流场参数。

初始条件下,波前靠近上壁面区域填充H2+O2预混可燃气(图1中灰色区域),远离上壁面区域填充H2+0.05N2轻质气,利用不同气体层的厚度比来定义充填比ε=l2∶l1。本文考察了不同来流马赫数Ma(以轻质气为准计算)和不同充填比ε条件下斜激波与气体界面的相互作用过程,相应的计算初始参数见表1。

计算域的上边界为无滑移的刚性壁面,其余边界均为零梯度边界条件。考虑到计算初期人为设置初始条件会导致波后界面出现RM不稳定现象,从而在界面上产生大尺度涡旋结构,这种结构是不真实的。为避免计算初期的非物理真实性,初始计算时,首先将上边界设置为零梯度条件,并关闭化学反应项,直至计算的大尺度涡旋结构流出上边界,再将上边界设为壁面条件,同时打开化学反应项,此时的波后流场即为真实流场,故可以进一步开展后继计算。

表1 算例及初始计算参数

2 计算结果与讨论

2.1 数值验证

本文采用均匀的正方形网格来离散计算区域,为验证网格精度,针对表1中的算例3(基准算例),选取了0.2 mm,0.4 mm及0. 8mm的3种网格精度进行数值模拟。图2给出了斜激波穿过界面后的激波角β2和点火燃烧(t=1.23 ms时流场发生燃烧)后比冲I*随计算时间的变化。

图2 不同网格精度燃烧后流场参数变化

由图2可以看出,0.4 mm网格的计算结果与0.2 mm网格的结果比较接近,而0.8 mm的网格则明显过低预测了激波角和比冲随时间的变化,因此,本文在后继计算中选择0.4 mm的网格尺寸,该尺寸可满足计算精度要求,每个算例中网格总数量为30万。

由1.2节可知,本文计算中初始阶段先要形成真实的冷态流场,然后在某一时刻打开化学反应项并设置上壁面条件。为进一步考察化学反应设置时刻对着火之后流场的影响,本文还模拟了不同化学反应设置时刻的燃烧场。图3给出了算例3不同化学反应设置时刻燃烧后流场的温度分布,可以看出,在相同的斜激波位置的情况下,2个燃烧场的波系结构、火焰界面的形状具有相似性。需要说明的是,由于火焰界面KH不稳定带来的随机性,2个算例的界面形状不可能完全相同,但其基本形态存在明显的相似性。这一结果表明,化学反应时刻的设置对流场最终的发展基本没有影响。因此,在后继计算中,均以打开化学反应项的时刻作为结果分析的起点(t=0)。

图3 不同化学反应设置时刻燃烧后流场温度分布

2.2 流场特性分析

2.2.1 来流速度对流场的影响

本文首先考察了充填比ε=3∶1的条件下,来流速度在2 000～2 750 m/s范围内的流场变化(表1中算例1～算例4)。数值模拟结果表明,当来流速度在2 500 m/s以上时,斜激波与气体界面的相互作用可以导致预混气的着火并诱发燃烧和爆轰。

图4给出了基准算例3在3个典型时刻的流场分布。图4(a)为着火刚发生时刻的流场分布,可以看出,着火发生在斜激波(OSW)于上壁面发生反射后的反射波(RSW)波后的位置,同时该位置也位于受扰动的气体界面(GI)附近。当t=1.37 ms时,着火已发展为爆轰过程,见图4(b)。这里流场存在2个明显特征:①在预混气体区(靠近上壁面区),燃烧是以预混形式的爆轰波(DW)发展的,此时,反应阵面(以温度分布表征)和激波阵面(以密度梯度表征)强烈耦合;②气体界面处的燃烧是以非预混燃烧的方式进行的,火焰阵面(NPF)具有小尺度涡旋结构。到t=1.46 ms时,见图4(c),燃烧进一步发展,爆轰波阵面逐渐向左传播,而界面处的非预混燃烧则逐渐表现为大尺度火焰面的形态。

图4 算例3的流场分布(u0=2 500 m/s,ε=3∶1)

图5给出了来流速度为2 750 m/s时(算例4),斜激波与气体界面相互作用后的几个典型时刻的流场分布。与图4类似,着火也发生在斜激波于壁面形成的反射激波波后,见图5(a),且着火燃烧之后的流场中也存在预混体系下的爆轰波和非预混体系下的火焰阵面,见图5(b)、图5(c)。然而,更大的来流速度会使斜激波的马赫数更高,因此,反射波之后的流场有着更高的温度和压力,故而会在更早的时刻着火(t=0.65 ms)。同时,更强的斜激波波后流体速度更快,会加剧界面的失稳过程,因此气体界面处的非预混火焰界面随着时间的进行呈现出更加明显的大尺度涡旋形态,这有利于将轻质气卷入燃烧区,从而加速已燃气和未燃气之间的混合。

当来流速度小于2 500 m/s时,斜激波与气体界面的相互作用不能导致流场发生着火现象。图6给出了来流速度为2 250 m/s时(算例2)流场发展后期(t=2.00 ms)的计算结果分布。从图中可以明显看到流场中存在的斜激波及其反射波,以及KH不稳定导致的带有涡旋结构的气体界面。此外,从图中也可以看出,在反射激波波后的区域也存在着高温区,但由于来流速度较低,该高温区的温度并不足以使可燃预混气达到着火温度,因此流场始终处于未燃烧的状态。

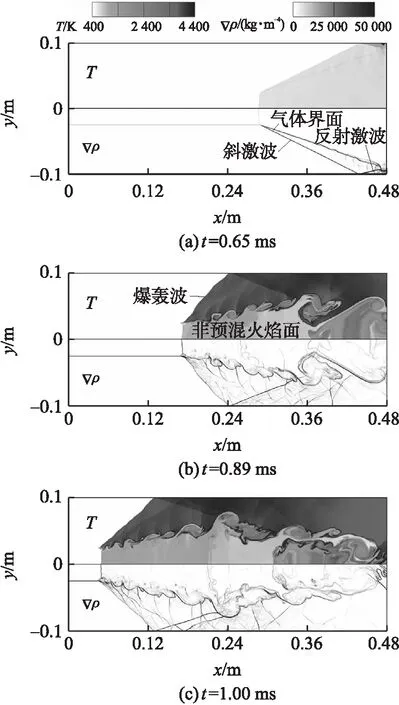
图5 算例4不同时刻的流场分布(u0=2 750 m/s,ε=3∶1)

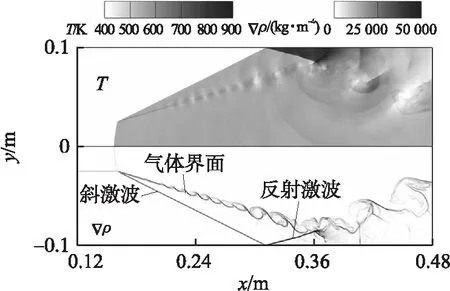
图6 算例2的流场分布(u0=2 250 m/s,ε=3∶1)

2.2.2 充填量对流场的影响

为考察充填量对流场反应性的影响,图7给出了充填比ε=2∶2的条件下,来流速度为2 500 m/s和2 750 m/s时的流场发展后期的结果。可以看出,在计算区域范围内,2种来流条件下的斜激波及其反射激波均逐渐沿来流方向右行流出流场。这一结果表明,尽管在ε=3∶1的条件下这2个来流速度可以引发着火和燃烧(见图4和图5),但在ε=2∶2时并未着火燃烧,可见充填量对预混气的着火过程有明显的影响。

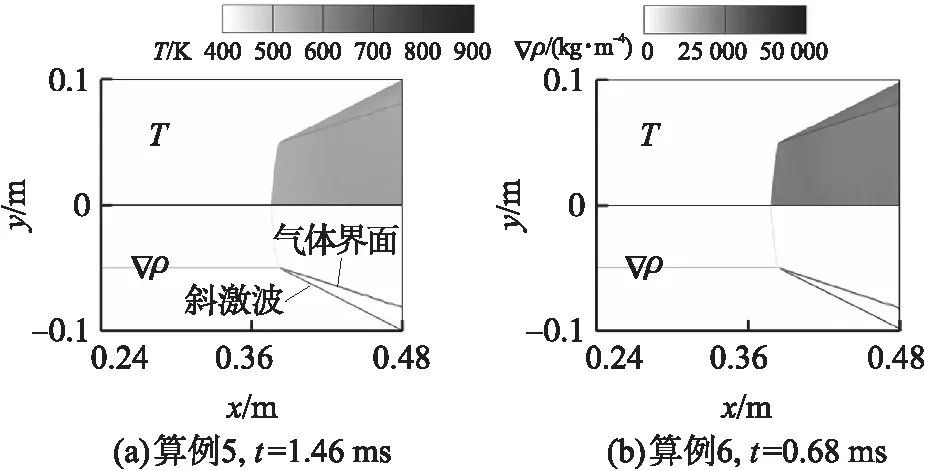
图7 算例5和算例6(ε=2∶2)的流场分布

为进一步分析充填量对着火过程的影响,本节选择了来流速度为2 750 m/s的算例(算例4和算例6),考察不同充填比条件下的流场差异。图8给出了2个算例在0.4 ms(算例4着火发生前的时刻)时的化学反应当量比ξ和涡旋结构的分布图的对比。这里ξ代表实际燃料的空燃比和等当量反应下的空燃比的比值。因此在本文条件下,初始预混可燃气的ξ=2,而轻质气的ξ=0,ξ的变化范围在0～2之间,ξ=1为等当量比条件。对流场中的涡旋结构,本文采用了文献[15]构造的新的涡识别方法(Rortex(Rz))来显示流场中的这一结构,该方法能够有效地提取流体质点的刚性旋转特性,从而有效地将旋转从剪切中剥离出来。图8(a)为t=0.4 ms时流场右半部分的涡结构与化学当量比分布图的叠加,右半图分别给出了流场局部的涡结构Rz和化学当量比ξ的分布图。

图8 算例4和算例6的涡结构Rz和化学当量比ξ的分布

从图8的结果来看,在来流速度相同的条件下,充填比不同导致了斜激波波后气体界面长度的不同。充填比ε=3∶1的算例,由于其预混气的厚度明显要大于ε=2∶2的算例,因此其受斜激波作用而发生偏转后的界面也明显长于后者。由于气体界面两侧气体速度的不同可导致界面发生KH不稳定从而产生一系列的涡结构,这些涡结构的尺度是沿界面向下游逐渐增大的。因此,对ε=3∶1的情况,由于其气体界面更长,所以向下游发展的涡尺度更大,更大的涡结构有利于预混气和轻质气的充分混合,从而创造了更多的接近等当量比条件的区域;另一方面,这些区域又接近于反射激波波后的位置,因此较高的温度条件(由来流速度决定)和合适的化学当量比(由充填比决定)保证了算例4能够有效地着火燃烧。

2.3 着火条件分析

从上一节的讨论可知,斜激波与气体界面的相互作用能否导致着火燃烧明显依赖于来流速度和预混气的充填量,这说明着火条件受到了流场中流动过程和化学反应的共同影响。为了进一步探索着火及发生爆轰的条件,本节引入了时间尺度的方法对着火条件进行定量分析。

定义tc为着火前某一时刻流场中最大温度处预混气的化学反应延迟时间,根据该处的温度、压力和预混气组成,采用Chemkin软件包[16]进行等容燃烧计算,取初始计算时刻到最大温升速率所在时刻为化学反应延迟时间。定义tf为流动时间,表示上述预混气微团以当前速度向右流出边界所需的时间,采用该预混气微团所在位置离出口边界的长度与该点水平速度的比值得到。显然,如果tc

图9给出了本文各算例的时间尺度曲线对比。

图9 各算例时间尺度对比结果

图9(a)和9(b)为能够发生着火燃烧的算例3、算例4的时间尺度曲线的对比。可以发现,初始时2个算例的tc均明显大于tf,表明开始阶段流动的作用大于化学反应,随着时间的进行,tc迅速减小,并最终小于或接近tf,这说明化学反应的作用在逐渐增大,并最终占据主导导致了着火的发生。比较图9(a)和图9(b)还可以看出,2种来流速度下tf的尺度差别并不大,但tc尺度的差别比较明显,即更大的来流速度有着更小的tc,这说明化学反应对来流初速的变化比流动过程更加敏感。

图9(c)～9(f)为未发生着火燃烧的其余4个算例的时间尺度对比曲线。各算例的流动时间尺度比较接近,算例1和算例2在10-1ms量级左右,而算例5和算例6在10-2～10-1ms量级之间。然而这些算例的化学反应时间尺度之间相差较大。尽管如此,对于图9(c)～9(f)中的所有算例,在本文模拟的时间范围内均有tc>tf,表明化学反应的作用始终小于流动过程的作用,因此不会导致最终流场的点火燃烧。从图9(c)和图9(d)来看,算例1和算例2较低的来流速度导致斜激波强度较低(见表1),所以反射波后的温度、压力较低,化学反应延迟时间较长;而从图9(e)和图9(f)来看,算例5和算例6较高的来流速度导致了较高的激波强度,因此初始时刻tc较小且有短暂的下降趋势,甚至算例5(图9(e))中tc曾一度接近tf,但是,由于这2个算例具有较小的充填量,气体界面的KH不稳定发展不够充分,导致其不能创造接近于等当量比的预混气组成,见图8,从而使得化学反应变慢,相应地,其tc不再继续下降,甚至还进一步增加。

2.4 推力性能分析

推力性能是考察冲压加速器工作特性的重要指标之一。针对本文的计算构型,计算了其推力F*和比冲I随时间的变化关系,其公式表达如下[17]:

(6)

(7)

式中:exit代表右边界,inlet代表左边界,ρ为轻质气密度,u为x方向的速度分量,p为轻质气压力,pb为外界反压;g为重力加速度。需注意的是,本文是二维流场计算,推力及比冲均为单位长度上的值,且由于弹丸在轻质气中飞行,所以本节考察的流场参数均来源于轻质气中。

图10显示了算例3和算例4(可点火燃烧的情况)的推力及比冲随时间的变化关系,图中,tig为每个算例各自的着火时间。可以看出:初始来流速度为2 500 m/s的算例3,在着火燃烧后初始推力和比冲均有一个明显上升,之后呈现逐渐下降的趋势;而初始来流速度为2 750 m/s的算例4在着火燃烧后推力和比冲基本上保持了相对稳定的变化,且推力和比冲明显高于前者。这表明更大的来流速度(弹丸运动速度)有利于更好和更稳定的推进性能。