非淹没刚性植被影响下孤立波在岸滩上的爬高

2019-03-26唐梦君唐政江蒋昌波

水利水电科技进展 2019年2期

姚宇,唐梦君,唐政江,蒋昌波,3

(1.长沙理工大学水利工程学院,湖南长沙 410114;2.河海大学海岸灾害及防护教育部重点实验室,江苏南京 210098;3.水沙科学与水灾害防治湖南省重点实验室,湖南长沙 410114)

海啸是由海底地震、火山爆发、海底滑坡或气象变化产生的破坏性海浪,海啸波与海岸相互作用后产生的海面爬高可能会给沿岸地区造成严重的洪涝灾害。对2004年印度洋大海啸的灾后调查研究发现,沿岸生长的红树林类刚性植被能对海啸波起到显著的削弱作用[1-2],培植海岸植被认为是未来一种积极的海啸防御措施。因此研究海啸波与红树林类刚性植被的相互作用对海啸灾害的防治具有一定的指导意义。

由于海啸波的首波与孤立波十分接近,因此学术界多采用孤立波来模拟海啸波的首波[3]。物理模型试验是研究孤立波与植被相互作用问题的主要手段之一,国内外学者在波浪水槽中对孤立波与平底海岸上刚性植被的相互作用问题进行了大量的研究工作[4-8],而关于孤立波与斜坡海岸上刚性植被的研究则相对较少。Irtem等[9-10]通过物理模型试验,研究了孤立波在非淹没刚性植被存在条件下的斜坡上的爬高问题,但未考虑岸滩坡度变化对刚性植被存在下孤立波爬高的影响。

植物的阻力系数一般难以直接测量[11],数值模型是获取植被阻力系数的一种可行的方法。对于长波与植被相互作用的模拟,常用的数值模型有求解浅水波方程的模型[12],求解Boussinesq方程的模型[4-5]和直接求解Navier-Stokes方程的CFD方法[13]，其中Boussinesq方程兼顾计算精度和计算效率,得到了较为广泛的应用。姚宇等[14]首次采用Boussinesq方程模拟了孤立波与斜坡上非淹没刚性植被的相互作用,并通过添加拖曳力项对植被阻力进行描述,得出了拖曳力系数随波高和植被密度的变化关系,但是尚未涉及不同斜坡坡度的情况。

本文拟在改进Yao等[10]物理模型试验的基础上,对非淹没刚性植被影响下孤立波在不同斜坡上的传播变形及爬高特征进行试验,并采用校核后的Boussinesq数值模型与试验结果进行对比验证,研究结果可为通过培植近岸植被来防治海啸灾害的实践活动提供参考。

图1 物理模型布置(单位：m)

图2 植被区域的排列方式

1 物理模型试验

长沙理工大学水利实验中心波浪水槽长45 m、宽0.5 m、高0.8 m,水槽左端配备有一台活塞式造波机,可产生包括孤立波在内的多种波况。物理模型在水槽中的布置如图1所示，岸滩斜坡采用PVC板来模拟,坡脚设置在距造波机17 m处,在距坡脚水平距离1.16 m的斜坡上布置有长0.6 m、宽与槽宽一致的植被区,区内单株刚性植物采用直径为1 cm,高度为30 cm的PVC圆管来模拟。将植株按照一定的排列方式垂直固定在预留孔洞的PVC板上(图2(a)),固定板悬挂于斜坡上方,植株的下端与斜坡接触并用玻璃胶固结(图2(b))。

植被排列的密度可采用固体体积分数φ=Vs/V进行计算,其中V为控制体体积;Vs为控制体中植被固体所占的体积。采用图2(c)所示的3种植株交错布置的方案,分别命名为排列A、排列B和排列C,密度分别为:φA=0.087、φB=0.109、φC=0.196。

设置坡度分别为1∶6、1∶8、1∶10的3种岸滩坡度,在改变坡度的过程中植被位置保持不变。测试水深固定为30 cm,入射波波高分别设置为2 cm、4 cm、6 cm、8 cm和10 cm,所有工况下植株顶部均处于非淹没状态。使用4个超声波浪高仪S1～S4测量自由液面的变化;采用CCD高速相机记录孤立波的爬坡过程,孤立波的爬高通过分析图像中波浪在标有刻度的斜面上的最大上爬位置而得。

2 数值模型模拟

采用一维高阶强非线性Boussinesq方程来模拟波浪沿礁的传播变形过程[15]。由于植株模型呈圆柱状,植被的阻力可采用拖曳力来描述。拟定x轴的正向为波浪传播方向,t为时间,仿照姚宇等[14]通过添加拖曳力项来模拟植被阻力,改进后的一维Boussinesq方程为

(1)

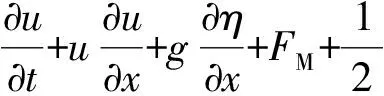
(2)

式中:η为自由液面的位移;h为平均水深;D为总水深,D=h+η；u为高程-za处水平方向速度(za=0.531h);up为植被区内沿x方向的孔隙流速;ρ为水的密度;dt为植株直径;Nt为单位面积内的植株数;Cd为植被拖曳力系数;τb为底床摩擦力;FC和FM为浅水波方程的Boussinesq校正项。

up与u关系通过下式确定:

(3)

式中:θ为斜坡角度。

τb可由曼宁系数n求得:

(4)

式中：g为重力加速度。

此外,由于沿水深积分的Boussinesq模型不能描述自由表面的翻转和详细的波浪破碎过程,因此需要添加半理论半经验的破碎波模型来模拟波浪破碎所造成的能量损失,以求更好地模拟波浪传播变形过程。破碎波模型采用Kennedy等[16]提出的涡黏模型。该模型中需设置4个经验参数,参照Lynett等[17]的建议取δ=6.5,α1=0.65,α2=0.08,α3=8.0。

3 模型试验与数值模拟结果对比分析

3.1 底床摩擦因数和植被拖曳力系数的校核

由于波浪在斜坡岸滩上的爬高受到底床摩擦的影响,首先必须对式(4)中的摩擦因数进行校核。校核的原则是选取有代表性的工况首先调整入射波高使S1测点的波高H1与试验测量一致,随后调整曼宁系数n使计算的S2～S4位置波高H2～H4以及岸滩爬高R与试验测量的符合程度达到全局最优,经校核得到n=0.003。图3比较了坡度为1∶6且无植被时H2～H4以及R间的实测和模拟结果,总体而言两者符合程度较好。

图3 无植被时波高和爬高的试验与数值模拟结果对比

除植被区外采用校核的摩擦因数,植被拖曳力系数的校核通过调整式(2)中的Cd值确定,校核的原则是使计算的透射波高H4与试验结果符合程度达到最优。考虑到对波高的测量较对爬高的测量更为精确,选用H4而不是R作为校核标准。各测试波高下校核得到的拖曳力系数Cd的平均值如表1所示。由表1可以看出,Cd值随着植被密度的增加而增加,随斜坡坡度的增大而减小。Cd的取值范围在1.5～3.5之间,与Huang等[4]孤立波与平底植物相互作用的范围1.5～2.5和Iimura等[5]孤立波与斜坡植物相互作用的范围0.6～2.2类似,一定的差异与植被密度不同及坡度不同有关。

表1 不同坡度时的平均拖曳力系数

3.2 自由液面时间序列的比较分析

图4 不同测点试验和数值模拟的η过程对比

图4为波高6 cm的入射波与植被排列B作用时,不同岸滩坡度S1～S4位置测量和模拟的自由液面η的历时曲线对比。图4表明:S1～S3位置测量的自由液面均存在3个明显的峰值,首先出现的为入射波波峰,随后出现的为植被区反射造成的反射波波峰,最后为岸滩反射造成的波峰,3个波峰在靠近远海侧(S1)且岸滩坡度最小时(1∶10)分开得最为明显;S4处仅存在透射波波峰和岸滩反射造成的波峰,这种反射波也是在岸滩坡度1∶10的时候更加明显。同时在反射波后面紧接着出现一个明显的水位降低,这是波浪回退的阶段产生了水跃现象造成。当岸滩坡度为1∶6时,S4位置岸滩高程位于静水位以上,故透射波传播到此时已接近爬坡的最高点,S4处除了透射波的主峰外,并无岸滩反射波和回落水跃现象。对于数值模拟而言,所采用的Boussinesq模型对于3种岸滩坡度的入射波峰的模拟较为准确,仅在反射波的模拟方面略有差异;此外沿水深积分的Boussinesq方程无法捕捉到S4处的回落水跃存在。

图5 无量纲透射波高H4/H1随H1/h的变化

3.3 透射波高的比较分析

图5为不同植被密度和岸滩坡度影响下,无量纲透射波高H4/H1随无量纲入射波高H1/h的变化规律。图5表明:对于所有植被排列和岸滩坡度而言,H4/H1随H1/h的增大而减小;对不同密度的植被排列进行对比发现,当入射波高一定时,透射波高随植被密度的减小而增大,这与表1中密度越小阻力系数越小的结论相对应;通过对比不同岸滩坡度发现,当植被排列相同时,岸滩坡度越大,透射波高亦越大,大部分工况的H4/H1>1,即出现透射波高大于入射波高的情况,这主要是由于坡度较陡时,波浪与斜坡上植被相互作用时过水面积减小导致阻水效应减小,且小于斜坡上由于波浪浅化作用造成的波高变陡。同时,图5中所有工况下的实测和模拟的透射波高吻合度均较好。

3.4 岸滩爬高的比较分析

图6 无量纲透射波高R/H1随H1/h的变化

图6为不同植被密度和不同岸滩坡度影响下,无量纲岸滩爬高R/H1随S1处无量纲入射波高H1/h的变化情况规律。图6表明:H1/h越小,R/H1越大;对比不同密度的植被排列表明,当入射波高和斜坡坡度不变时,岸滩爬高随着植被密度的减小而增大,这与3.3节的结论一致,均是由于植物密度的增大加强了植物的阻水效应造成[14],这也与表1中拖曳力系数随着植被密度的增大而增大的现象一致。当对比不同岸滩坡度的爬高发现,虽然S4处透射波高在坡度陡时较大(图5),相同的植被排列在相同的入射波作用下的无量纲爬高并无显著差异,这是因为陡坡的存在抑制了透射波在岸滩上的进一步上爬,造成不同岸滩坡度间的爬高值比较接近。总体而言,所采用的数值模型能较好地模拟植被区后岸滩上孤立波的爬高变化规律,对某些工况存在一定的误差,可能是物理模型试验中干湿分界线沿槽宽分布不均造成的测量误差所致。