基于SPH法的正弦形消力池底板水跃现象数值模拟

薄夫萍，吴海涛，王 星，张云云，顾声龙

(青海大学水利电力学院，青海 西宁 810016)

水跃是底流消能工中常用的消能形式。经过水跃这一局部水力现象，水流流态发生急剧变化，水跃区段内底部主流区和上部旋滚区相互掺混、碰撞、摩擦，下泄水流消耗大部分动能从而使流速锐减、流态趋于平稳，以达到消能效果。但当消能率较低时，下泄水流经消力池后仍携带大量余能，致使下游河床遭受严重冲刷甚至造成坝体损坏[1]。因此，提高消力池的消能率是目前水工结构设计中迫切需要解决的问题。

正弦形消力池底板最初由Ead等[2]提出，其本质是将光滑的消力池底板改为正弦形以增加壁面粗糙度，使水流之间的紊动更为剧烈，水跃特性急剧改变，从而增加消能率。目前对此种消力池的研究方法主要有试验研究、理论分析、数值模拟。Hughes等[3]通过对消力池底板加设不同砾石的试验研究表明，随着底板粗糙度的增加，水跃跃长明显缩短，消能率有所提高；Tokyay[4]、Izadjoo等[5]、Abbaspour等[6]、Elsebaie等[7]、Samadi等[8]分别通过大量试验研究了正弦形、梯形、三角形底板上的水跃，指明共轭水深是与弗劳德数(Fr)有关的函数，且正弦形底板在消能方面具有很大潜力。傅铭焕等[9]、张志昌等[10-11]结合断面流速分布对数规律及动量方程给出了共轭水深、水跃长度等理论计算方法，并指出壁面阻力对波状底板水跃特性有很大的影响，是解决实际问题中不可忽略的重要因素。由于试验研究受到仪器、测量方法等因素的限制，很难准确测量复杂水力现象中急剧变化的参数；而理论分析需对研究问题做大量假设以简化控制方程便于求解，但与实际现象偏离且求解过程繁琐，且参数选取主要基于经验公式。数值模拟则可以弥补试验研究及理论分析的不足，记录现象演变的全过程，为所研究问题提供完整、具体的数据，便于细部结构的观察，有利于揭示现象变化的本质。目前研究正弦形底板水跃现象采用的数值模拟方法主要为网格方法：魏文礼等[12-13]、程香菊等[14]、Abbaspour等[15]采用网格法建立不同形式的湍流模型，对波状底板上的水跃进行数值模拟，得到水跃的演变过程及近壁面处存在的小涡分布。但网格法由于受到网格节点的限制，在模拟自由表面、运动交界面、大变形等引起网格严重变形的多尺度问题时精度和准确性差强人意。而水跃现象中水流紊动剧烈并伴随空气不断地掺入[16]，自由表面存在旋滚，因而水面波动大且水体破碎严重，因此考虑采用新的数值模拟方法即光滑质点水动力学法(SPH方法)进行研究。SPH方法是纯拉格朗日形式的无网格粒子法之一，对需要计算的问题域采用任意分布的粒子框架进行描述，在处理大变形等问题上具有独特优势，目前已广泛地应用于滑坡涌浪[17]、多相流[18]、溃坝[19]、溢洪道[20]等工程流体动力学问题的研究，并取得了重要的成果。

结合水跃的特点及SPH方法的优势，笔者将使用SPHYSICS_2D软件对正弦形消力池底板上水跃现象建模计算，以分析其水面线、流速分布、跃长、共轭水深、消能率等水跃特性相较于光滑底板的变化趋势。

1 经SPH方法离散后的N-S方程

流体动力学中通常使用边界条件、初始状态结合质量、动量、能量三大守恒定律建立控制方程，以确定流体系统的运动情况。对无穷小流体单元采用拉格朗日描述法建立控制方程可得偏微分形式下的连续性方程、动量方程、能量方程，即N-S方程：

(1)

(2)

(3)

式中：α、β表示坐标方向；ρ为流体密度；t为时间；V为流体速度向量；X为流体位置向量；g为重力加速度；e为流体能量；σαβ为总应力张量；P各向同性压力；θ为黏性项。

SPH方法中将任意函数改写为SPH形式需要通过核近似、粒子近似2个关键步骤。经核近似后得场函数积分表示(式(4))，经粒子近似后得函数的离散形式(式(5))：

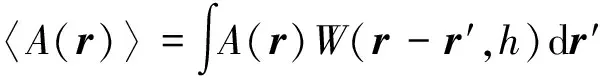
(4)

(5)

其中Wij=W(ri-rj,h)

式中：A(r)为任意函数；W(r-r′,h)为光滑函数；h为光滑长度，用以控制计算域;r和r′代表粒子位置；N为粒子总数；mj和ρj分别为j粒子质量和密度；Wij为i、j粒子间的光滑函数。

SPH方法中采用亚粒子模型(SPS)建立湍流模型，该模型由大涡模型(LES)和亚网格尺寸模型(SGS)组合而成。对黏性项θ的处理采用SPS方法，可得动量方程(式(6))；在SPH方法中流体被认为是弱可压缩性的，因此为控制流体的压缩性引入了状态方程(7)，通过改变声速调节数值模型时间步长以满足压缩性调节要求。但是声速也不能过小，至少是流体最大流速的10倍，这样才能确保粒子密度变化率小于1%，控制流体为弱可压缩状态。

(6)

(7)

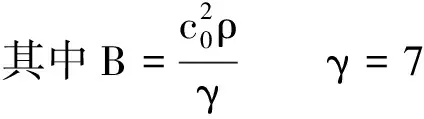
式中：ρ0为预设密度，取值为1 000 kg/m3；c0为预设密度对应的声速;ϑ0为层流动力黏度，取10-6m2/s；τ为黏性应力。

综上所述，经SPH方法离散后的N-S方程分别为以下形式：

(8)

(9)

(10)

式中：下标a、b表示计算域内任意2个粒子；mb为b粒子的质量；Vab为a、b粒子之间的相对速度向量；Wab为a、b粒子间核函数梯度；ψab为经SPH方法离散后的黏性项。

水跃消能率的计算通常使用跃前断面能量E1与跃后断面能量E2之差作为能量损失值ΔE，因此可以得到跃后能量损失为

(11)

式中：Z1、Z2分别为跃前断面、跃后断面水位高度；α1、α2分别为跃前断面、跃后断面的动能修正系数;U1、U2分别为跃前断面、跃后断面平均流速；P1、P2分别为跃前断面、跃后断面压强。

当渠底水平时，根据总流的动量方程可以推导出单宽流量q与跃前水深y1、跃后水深y2之间的关系,从而得到光滑底板上能量损失ΔE及消能率η：

(12)

(13)

2 水跃现象数值模型

为验证SPH方法研究正弦形底板上水跃现象的可行性及适用性，选取文献[2]中的试验数据与SPH模拟值作对比。文献[2]中试验模型使用的矩形水槽采用有机玻璃制作，宽0.446 m、高0.6 m、长7.6 m，并在水槽底部铺设铝制正弦形波状底板。试验布置如图1所示，图中Lj为跃长；Lrj为旋滚区长度；Um为断面最大流速；S为波长，T为波幅。研究的波形有2种：S均为68 mm，T分别为13 mm、22 mm。由于正弦形底板凹凸不平，易引发空蚀问题，Ead等[21]研究发现将正弦形底板设置在光滑水平面以下，波峰与光滑底板位于同一高度时，能有效避免壁面凹凸不平引起的空蚀问题。

图1 试验布置示意图[2]

根据试验模型采用SPHYSICS_2D软件建立相应的数值模型，如图2所示。模型主要结构包括蓄水池、水槽、尾水收集池。正弦边界采用公式y=Asin(π/0.034x)建立，当参数A(A为波幅的1/2)分别为0.006 5和0.011时可得T分别为13 mm、22 mm，S为68 mm的正弦形底板。模型由2种粒子构成，分别为可流动的水粒子和固定边界粒子。各工况闸孔自由出流流量调节通过蓄水池的水位调节实现；流经水槽的水流暂存在收集池以防水粒子运动到计算域以外，对数值计算产生干扰。建模时为减小运行时间预先在整个水槽段添加一定深度的水域。

图2 数值模型示意图

对文献[2]中5组工况进行数值模拟，具体参数如表1所示，表中y2*为光滑壁面跃后水深。数值运算时选取的主要参数如下：核函数为5次样条函数；黏性项处理采用亚粒子湍流模型；边界采用动力边界条件。模型粒子总数为96 476个，其中边界粒子4 610个，初始粒子间距为5×10-3m，光滑长度为3.68×10-3m,时间步长为0.01 s，模拟时长为10 s。

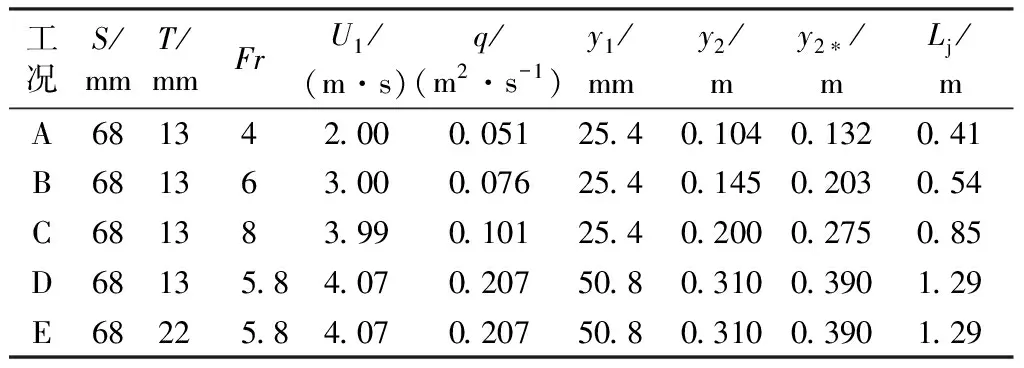
表1 工况参数

3 结果分析

3.1 模型验证

由于本数值模型只能在初始状态添加水域进行计算，故为满足试验工况所需的恒定入流条件，数值建模时在水池中添加一个推板，即推板模型[22]。通过设定推板的速度对闸口附近水域进行补给，以保证蓄水池中水位恒定。分析得知各试验工况闸口处流量的SPH模拟值与物理模型试验值间的误差分别为3.9%、6.6%。由流量对比(图3)可得：推板模型能够在短时间内达到各工况所需的稳定流量且流量值出现波动的情况较少，表明推板模型能够有效解决正弦形底板水跃研究中的流量恒定问题。

将工况A的SPH水面线模拟值和已有文献试验值及模拟值作对比,如图4所示。由图4可得各工况水面变化趋势基本保持一致，SPH数值模拟结果能够充分展现水面线形态的变化。

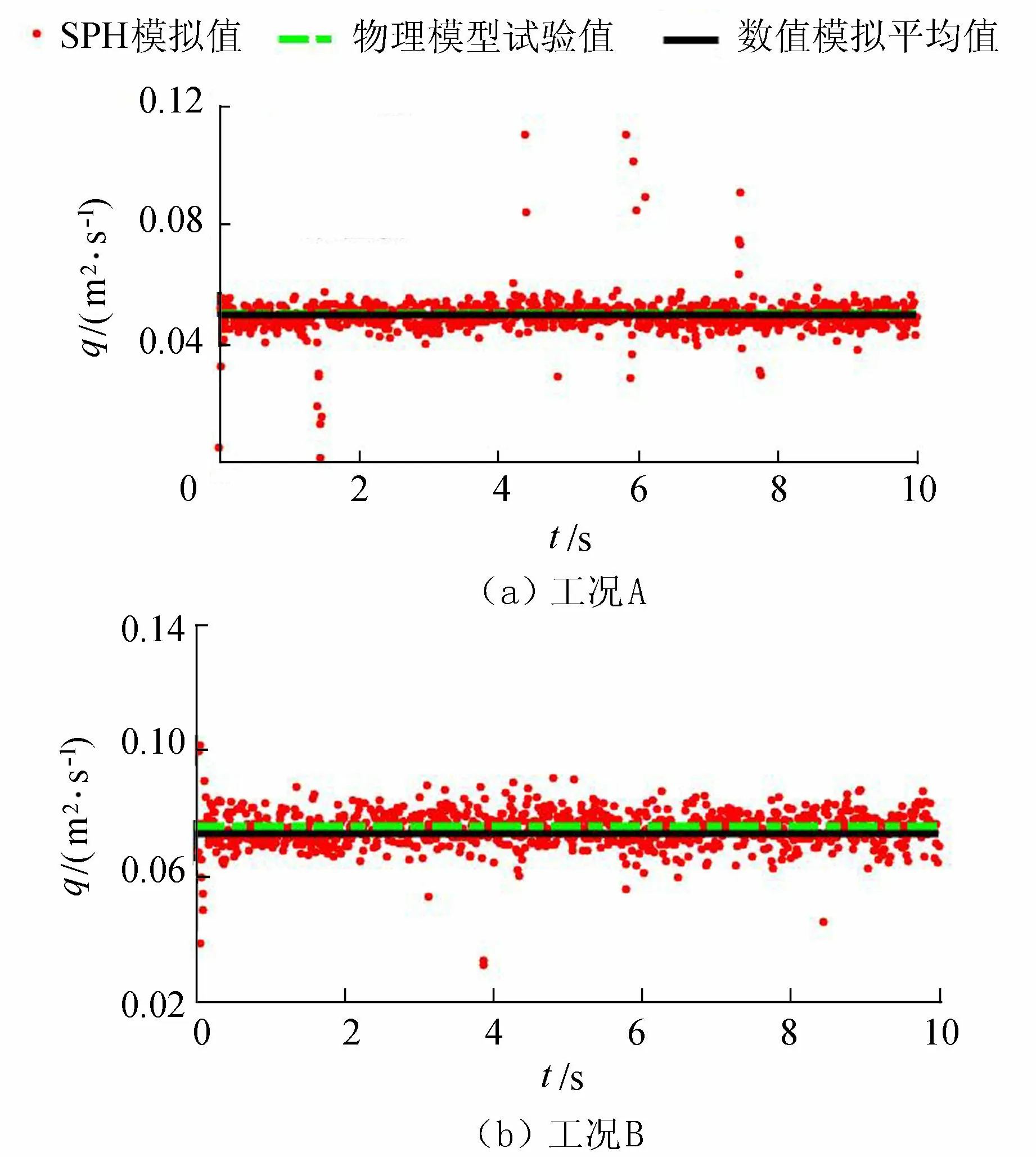
图3 闸口处流量对比

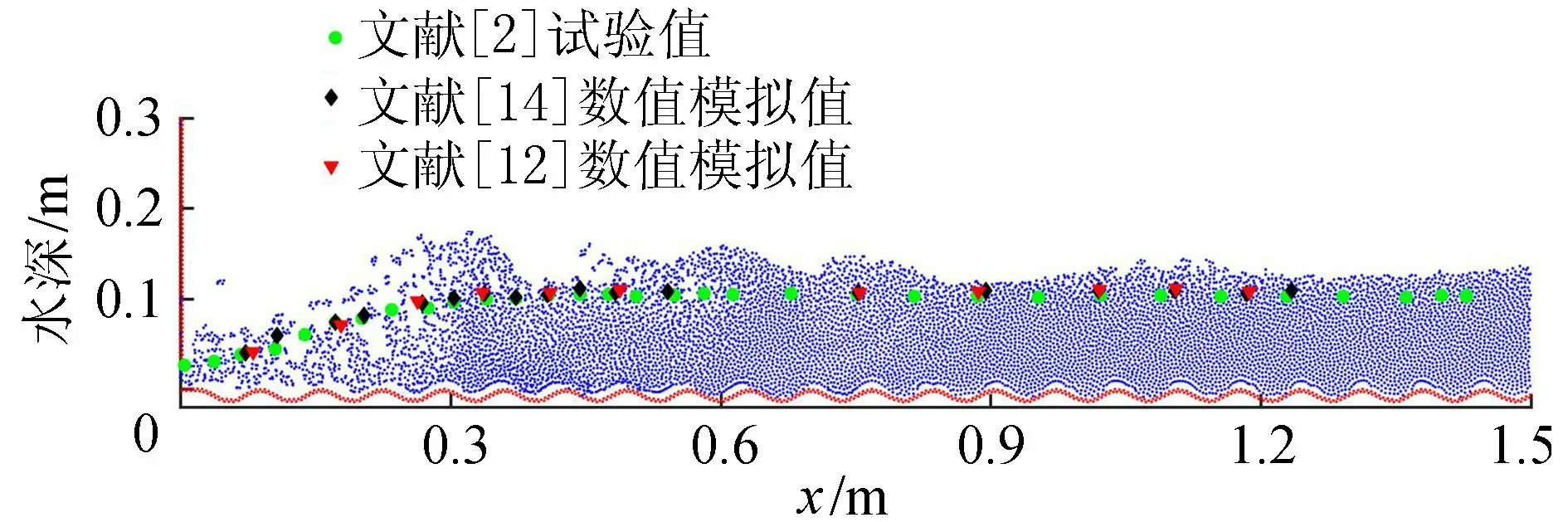
图4 工况A水面线对比

将5种工况水面线的SPH模拟值与文献[2]试验值作对比,如图5所示，可知两者基本吻合，仅在某些工况，如工况B、C旋滚区段水面有一定的偏差。考虑到水跃是一种较为复杂的流态，在水跃区段内主流区和旋滚区之间的水质点不断掺混，伴随大量的气泡产生或掺入，导致水面剧烈波动，部分粒子飞溅，造成试验值存在较大误差。工况D和E流量相同、波形不同时，水面线变化趋势基本相同，水面线基本重合，说明波形的改变对水面线高度的影响较小，分析其原因可能是由于波状底板位于水平面下方，没有伸入流体内部；且水面的高度远大于波状底板波幅值，故导致正弦形底板上波形的变化对水面线影响相对较小。

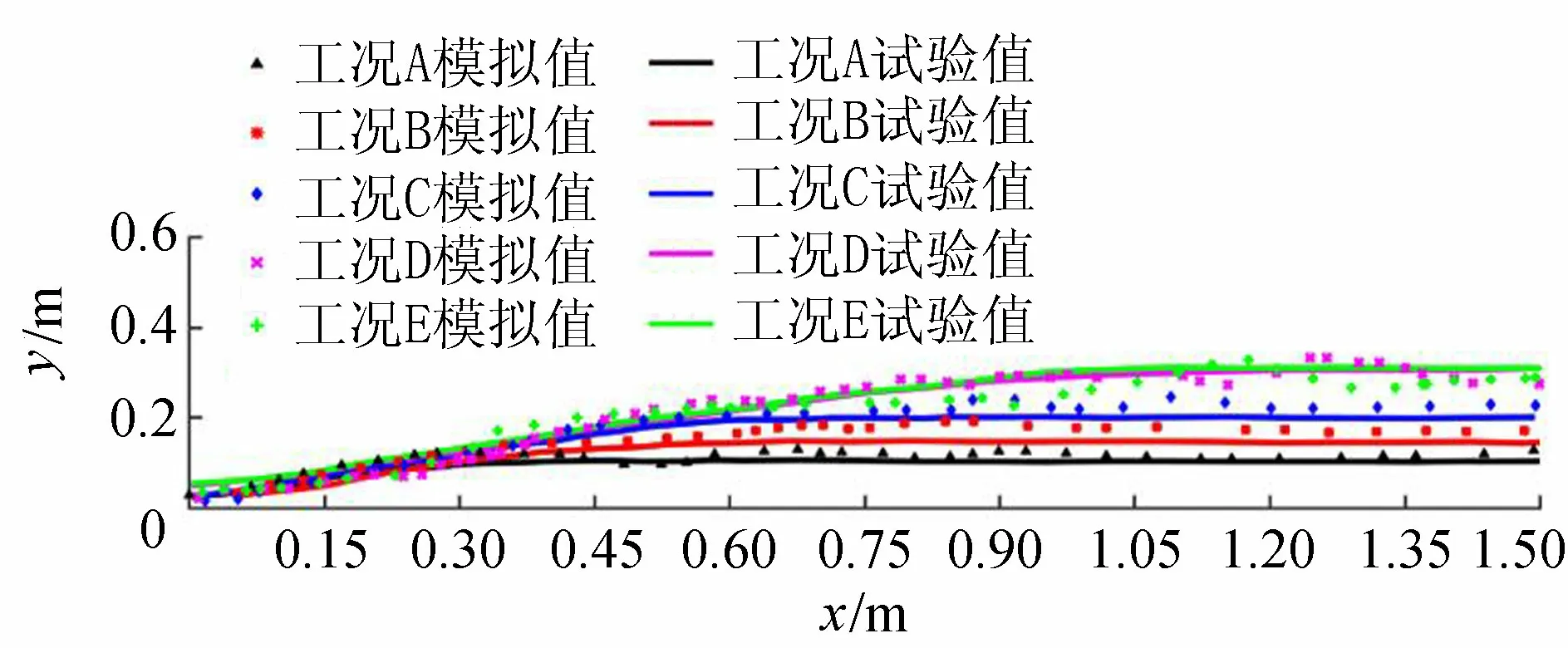
图5 各工况水面线对比

从5种工况水面线的整体情况来看，SPH数值模拟结果和试验结果吻合较好，说明SPH方法能够较为准确地反映水跃过程中水面的变化趋势及形态，在处理波状消力池底板上的水跃特性方面具有适用性及可靠性。

3.2 速度云图、矢量图

由工况A速度分布(图6)得：水跃段包括速度为正的顺流及速度为负的逆流，其中逆流主要聚集在水流表面和底部的主流处，表面由于部分水流回流形成逆流，底部因正弦形底板的波状结构形成波内旋涡导致流速为负；水跃段存在表面旋滚，且有大量气体掺入，速度分布波动较大，当底板为正弦形时波内形成旋涡，相当于增加了边界层的厚度和粗糙度，近壁面及表面流速较小，中间层流速较大；当水流流经明渠段时受边界层影响，表面流速最大，近壁面处最小。

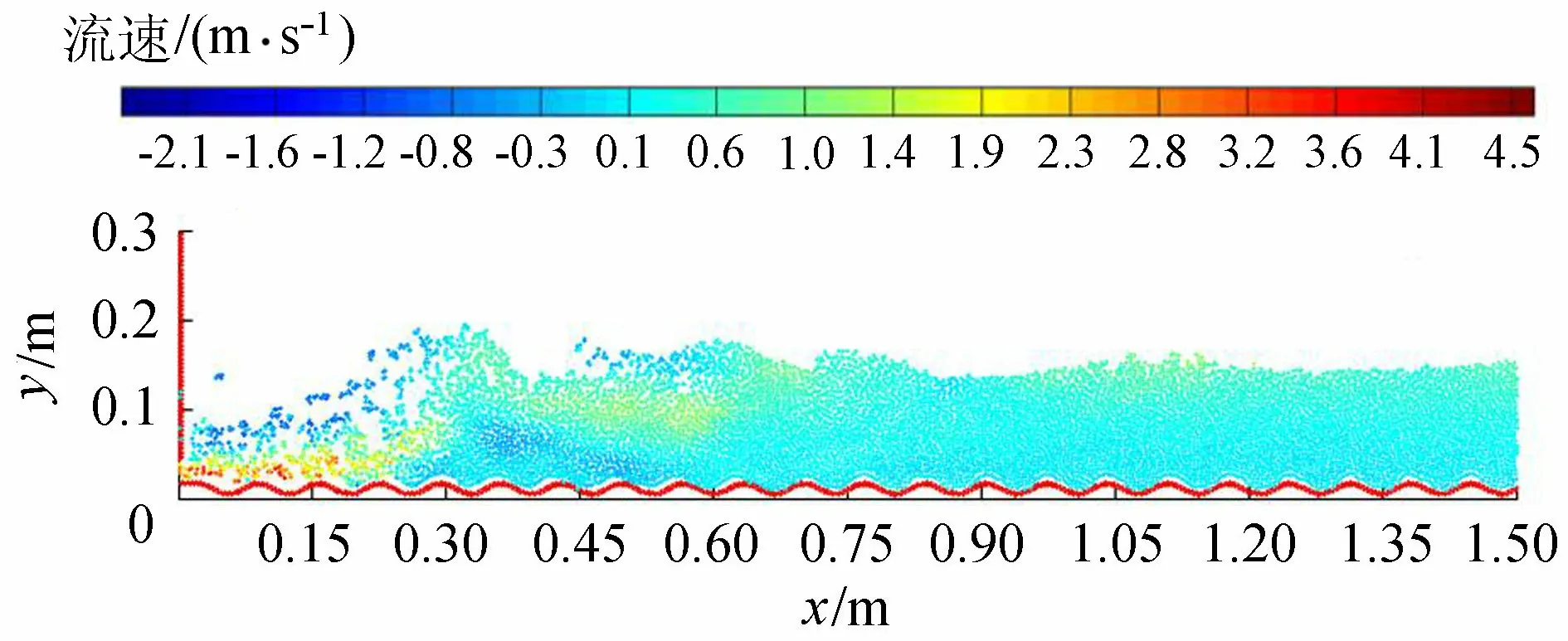
图6 工况A速度云图

图7 工况A速度矢量

图8 工况B速度矢量

结合工况A、B的速度矢量(图7、图8)可得：水跃段内有明显水流破碎和掺气现象；在闸口开度相同时，随着Fr的增大，水流破碎、掺气现象加剧并且存在明显涡结构，分析其原因主要是水跃段流速分布不均匀，流层间的水质点有相对运动，导致流层间产生的内摩擦切应力在水流表面为顺流方向，而在水流底部为逆流方向，故形成了顺时针流向的旋滚。对比两工况旋滚得：同等条件下旋滚倾斜程度随Fr的增大逐渐增加，即形成旋滚的长度逐渐缩短，旋滚内的涡结构愈发明显，涡团尺寸逐渐增加，这将意味着旋滚的影响范围逐渐变大。

3.3 跃长

水跃段水流剧烈翻滚掺混使水面形态急剧变化，旋滚的尾部水流不断汇入主流并被逐渐淹没，直到水流表面不会因为水流的翻滚而产生较大波动时流态演变为明渠流动。根据图7可得，水跃前部1—1断面至形成旋滚的2—2断面之间的距离为旋滚区长度Lrj；1—1断面至水流经过旋滚又回到较为稳定的自由水面3—3断面之间的距离为Lj。

将5种工况Lrj、Lj模拟值与试验值及光滑底板跃长试验值Lj*对比得出,Lrj、Lj模拟值相比对应试验值的误差分别在7%、8%以内；Lj试验值较光滑底板减小30%左右，表明正弦形底板上的跃长较光滑底板明显缩短，若应用在实际工程中能够有效缩短消力池长度。结合表1对比工况A、B、C的Lrj、Lj如图9所示，表明试验值和模拟值变化趋势是一致的；且同等条件下，Lrj、Lj均随着Fr的递增呈递增趋势。

图9 跃长、旋滚区长度对比

3.4 跃后水深

图10 共轭水深、跃后水深对比

将图7中水面变化较稳定的3—3断面处水深值作为跃后水深y2。为比较共轭水深与跃后水深的关系，将A、B、C这3种工况的共轭水深值统一缩小至原来的1/10与其跃后水深y2绘制在图10中，对比y2模拟值与试验值及光滑底板跃后水深y2*得：共轭水深、跃后水深的变化趋势相同；y2模拟值与试验值之间的误差在15%以内，y2试验值较y2*减少30%左右；比较工况A、B、C得同等条件下y2、y2*随Fr的增加而增加；结合表1中工况D、C可发现波形对跃后水深影响较小。采用无量纲分析法探究跃后水深、共轭水深与跃长间的相互关系。结果表明：y2和Lj变化趋势呈正比关系；当共轭水深呈递增趋势时，跃长呈减小趋势，两者呈反比关系，表明波状底板虽然能够减小跃长及跃后水深，但是不能同时减小共轭水深和跃长。

3.5 消能率

水跃消能是泄水建筑物中常用的消能形式之一，高速水流经过消力池后形成水跃，跃后流速的急剧衰减消耗了上游水流的大部分能量，从而起到消能的目的。因此，在工程造价预算范围内对消能工进行合理设计，以尽可能地提高消能率。

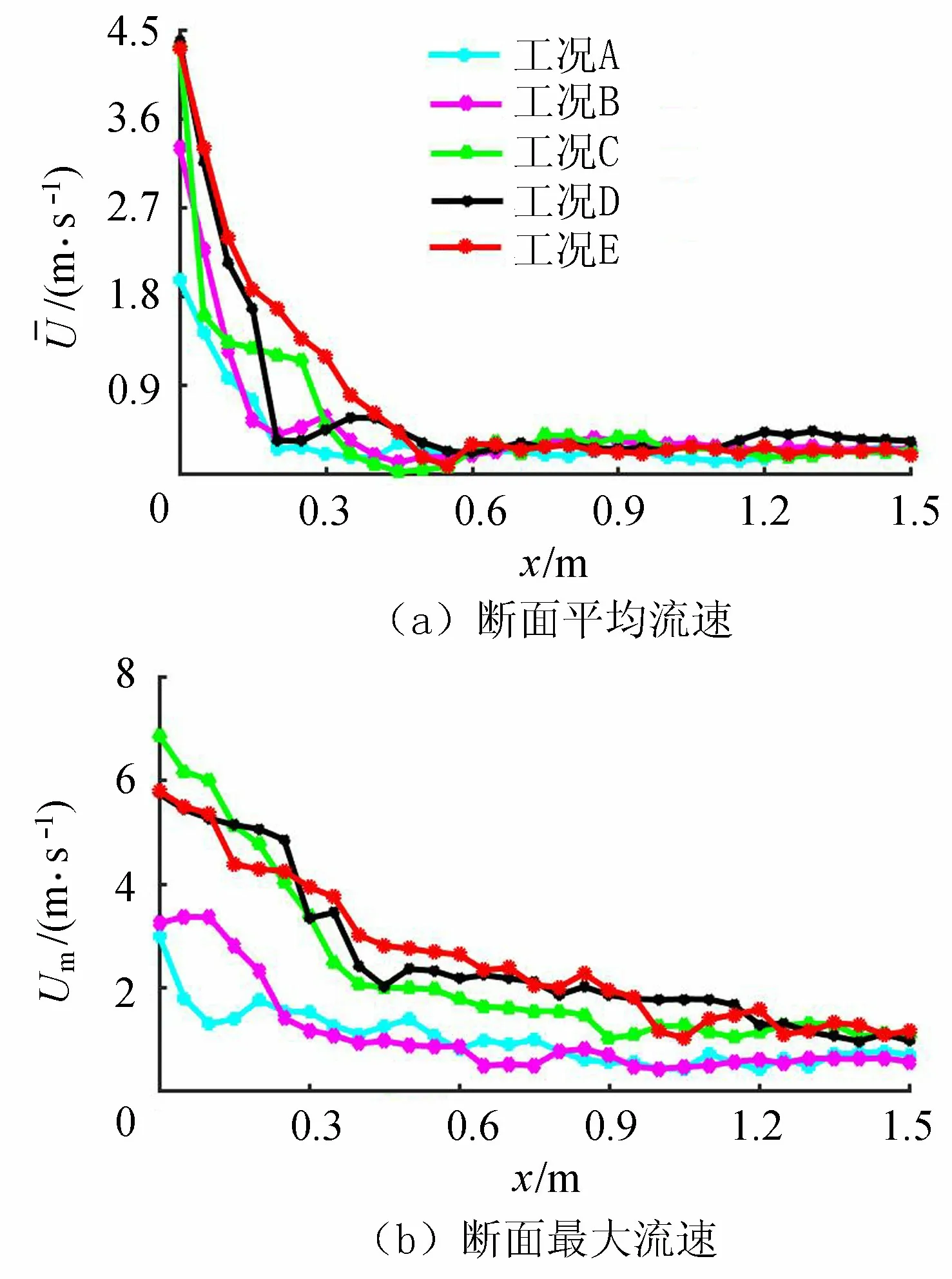
图11 流速分析

将5组工况正弦形底板消能率模拟值、试验值及光滑底板消能率进行对比，见表2，可知当Fr=4～8时，光滑消力池底板的消能率范围为39.36%～66.12%，正弦形消力池底板的消能率范围为47.08%～73.12%，因此正弦形底板较光滑底板消能率明显提高了10%左右，且5种工况的消能率均在47%以上。由表2还可得知，消能率试验值和模拟值吻合度较高，变化规律相似。在所研究的Fr范围里，光滑底板和正弦形底板的消能率均随Fr的增加而增加；对比工况A、B、C可得，当波形相同时消能率随Fr的增加而增加；对比D、E两种工况可得当Fr相同时，正弦波形不同时消能率较为接近，说明其他条件相同时，正弦波形对消能率的影响不明显，正弦形底板消能效果明显。

表2 各工况不同Fr时的消能率

4 结 论

a. 推板模型能够获取试验所需的恒定流量条件，使模拟流量误差在7%以内；流量能在较短的时间内达到稳定且很少出现数值波动。

b. 数值模拟水面线与试验值基本吻合，仅存在较小波动，验证了SPH方法研究正弦形底板水跃现象的可行性及适用性。

c. 水跃段流速分布不均匀且波动较大；相同条件下，随着Fr的增加掺气量及水面破碎现象越来越明显，旋滚的影响范围逐渐变大。

d. 正弦形底板跃长、跃后水深较光滑底板均较小30%左右，表明波状底板能够有效降低跃后水深，减小消力池护坦高度；对比模拟工况发现水面线、跃长受波形影响较小；跃长、跃后水深的变化趋势一致，但共轭水深与跃长变化趋势相反，故不能同时减小跃长和共轭水深。

e. 所模拟工况断面平均流速、最大流速分布规律具有相似性，即在水跃段存在较大波动、衰减，明渠段基本保持稳定；正弦形底板消能率较光滑底板提高10%左右，且5种工况消能率均在47%以上。