基于LSTM神经网络的水电站短期水位预测方法
2019-03-26刘亚新樊启祥尚毅梓樊启萌刘志武
刘亚新,樊启祥,尚毅梓,樊启萌,刘志武
(中国长江三峡集团有限公司,北京 100038)
准确的水位预测是水电站安全运行和增发效益的关键。然而,受诸多因素的影响,水位预测常常较实际情况偏差较大,导致发电计划频繁修改,不利于电站安全、高效、稳定地运行。特别是具有紧密水力联系的梯级电站,如三峡水电站和葛洲坝水电站构成的梯级电站,上游电站的出库流量预报误差会叠加到下游电站,且因两坝间往复流、出入库不平衡等问题,使得下游电站水位的准确预测更难实现。
大量学者对水位预测问题进行了研究,提出了多种预测模型。王蒙蒙等[1]基于支持向量回归模型对洞庭湖水位进行了预测,其输入变量为三峡水库逐日出库流量、清江逐日流量及洞庭湖“四水”逐日入湖流量。马辉等[2]提出了一种将灰色模型与神经网络相结合的灰色-BP神经网络预测方法,得到了较高精度的预测结果。李欣等[3]综合考虑河流水位时空信息,建立了基于时空序列的径向基函数(RBF)神经网络预测模型,预测了金沙江下游向家坝水文站的水位情况。余开华[4]提出了小波神经网络河道流量水位预测模型,并应用于预测盘龙河天保站的水位。Ashaary等[5]采用BP神经网络预测了Timah Tasoh水库的水位变化,采用窗处理的方式将前w个时刻的水位数据作为输入变量,建立了6个不同的神经网络模型进行比较,结果表明当w=2时,所建立的神经网络模型最优。Chang等[6]采用自适应神经模糊推理系统建立了水库水位的预测模型,并将其应用于Shihmen水库的水位预测,结果表明该模型可以准确预测连续3 h的水位。
但在梯级电站的水位预测方面,尤其是下游电站的水位预测,国内外进行的研究较少。由于梯级电站之间的紧密联系,上游电站的运行情况会影响到下游电站的水位,并且因距离的原因使得影响具有时间滞后性,因此在预测时要综合考虑这些影响因素。长短时记忆(long short-term memory, LSTM)网络是循环神经网络中一种带有门控的网络,能够考虑到数据的时序性特点,学习到数据之间的长期依赖关系,在处理时间序列数据的预测方面具有独特的优势,已被广泛应用于自然语言处理、语音识别、图片描述等领域。王鑫等[7]将LSTM用于航空领域的月度故障时间序列的预测,并提出了基于多层网格搜索的LSTM预测模型参数优选方法。保罗等[8]考虑磨机特征样本之间的时间尺度信息,采用编码神经网络的方法提取样本特征,使用LSTM建立了负荷参数的预测模型。Wielgosz等[9]将深度学习算法应用于大型强子对撞机超导磁体的监测和故障保护,分析了不同的LSTM网络结构和超参数对模型预测效果的影响,结果表明记忆单元为128,历史步长为16时效果最佳。杨训政等[10]将LSTM用于发电机组的污染物排放研究,并与最小二乘法、支持向量回归机进行对比,结果表明LSTM明显优于其他两种方法。
本文提出一种基于LSTM网络的水电站水位预测方法,并将其应用于预测葛洲坝水电站上下游水位,以期为葛洲坝水库的实时调度提供技术支撑。
1 基于LSTM神经网络的水位预测模型
1.1 循环神经网络与LSTM
循环神经网络在时间序列预测方面具有独特的优势,其通过特定的网络结构,将过去时刻的影响反映到当前的预测之中,同时由于共享不同时刻的权值矩阵,减少了参数数目,使得训练效率大大提高,并且可以处理任意长度的时间序列数据。尽管理论如此,但实际上,原始的循环神经网络由于参数共享,经过多阶段传播后的梯度倾向于消失或爆炸[11-12],使得模型丧失了学习到更早信息的能力,这个问题也称为长期依赖问题。1997年Hochreiter 等[13]提出了LSTM网络,很好地解决了这一问题。LSTM通过引入门的设置来决定控制信息的流动,最初LSTM只有两个门,即输入门和输出门,2000年Gers等[14]对其进行了改进,加入了遗忘门使LSTM通过自主学习遗忘一些无关紧要的历史信息。之后Gers等[15]提出了加入“窥视孔连接”的 LSTM变体,将单元状态也作为门的输入。Cho等[16]将遗忘门和输入门合并为更新门,提出了GRU(gated recurrent unit)模型。
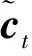
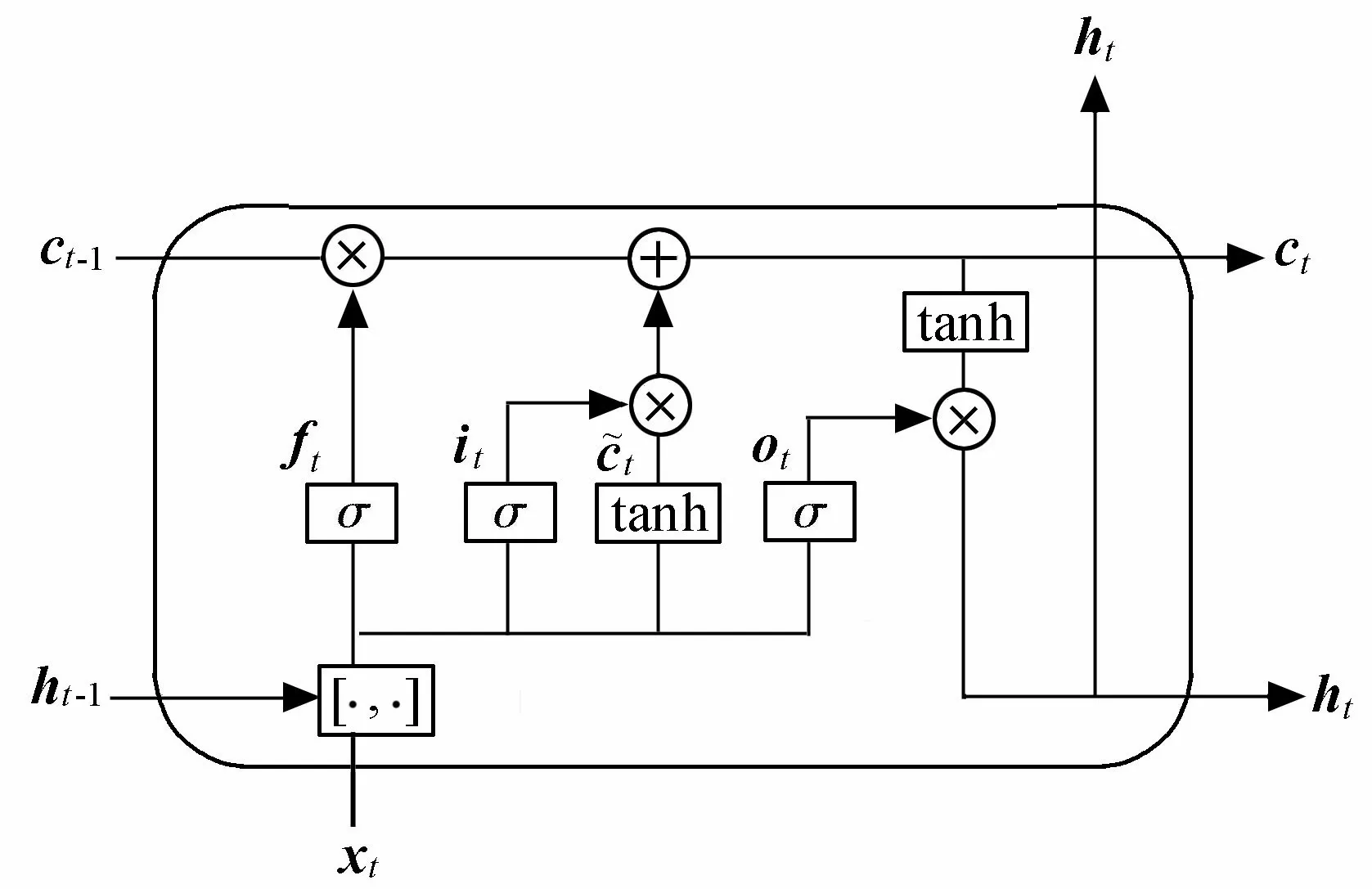
图1 LSTM的隐含层结构
1.2 LSTM的前向传播过程
正如图1所示,LSTM中的每个门实际上就是一个全连接层,输出是[0,1]之间的向量,用以控制信息的传递。门的激励函数σ为sigmoid函数,可表示为
(1)
根据应用的不同,LSTM可以有不同的变体形式。本文构建的LSTM结构如图2所示,每一个时间步都有输出,隐含层结构如图1所示,并且隐含层单元之间有循环连接。
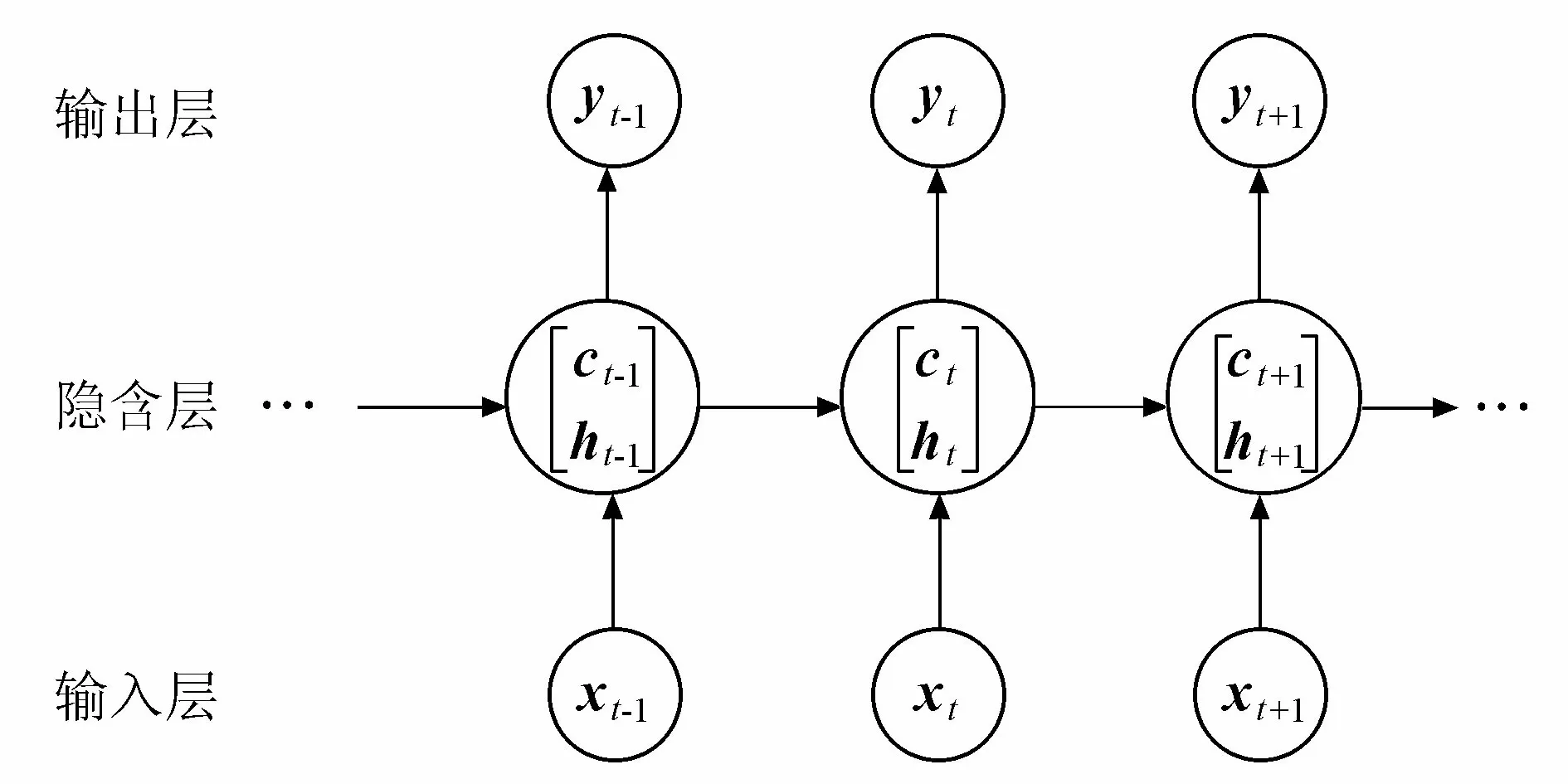
图2 LSTM的基本结构
图1和图2对应的LSTM的前向传播的具体公式为
遗忘门ft=σ(nf,t)
(2)
输入门it=σ(ni,t)
(3)
输出门ot=σ(no,t)
(4)

(5)

(6)
隐含层输出ht=ot∘tanh(ct)
(7)
输出层yt=tanh(ny,t)
(8)
其中nf,t=Wfhht-1+Wfxxt+bf
ni,t=Wihht-1+Wixxt+bi
no,t=Wohht-1+Woxxt+bo
ny,t=Wyht+by
式中:Wfh和Wfx分别为遗忘门中与ht-1和xt对应的权重矩阵;Wih和Wix分别为输入门中与ht-1和xt对应的权重矩阵;Woh和Wox分别为输出门中与ht-1和xt对应的权重矩阵;Wch和Wcx分别为当前输入的单元状态中与ht-1和xt对应的权重矩阵;Wy为输出层中与ht对应的权重矩阵;bf、bi、bo、bc、by分别为遗忘门、输入门、输出门、当前输入的单元状态、输出层中的偏置向量;∘表示两个向量对应元素相乘。
1.3 LSTM的误差反向传播过程
LSTM的训练算法仍然是误差反向传播算法。由于LSTM的前向传播过程是从左到右的有序传播,因此误差反向传播过程也是沿时间反向传递,称为BPTT(back-propagation through time)算法。
在本文构造的LSTM中,要训练的参数包括权重矩阵Wfh、Wfx、Wih、Wix、Woh、Wox、Wch、Wcx、Wy和偏置向量bf、bi、bo、bc、by。将误差沿时间反向传播,需要计算每个时刻的误差项。设t时刻真实值dt与估计值yt的误差为yt-dt,1到T时刻的总误差E可表示为
(9)
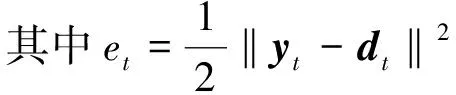
(10)
进一步可得
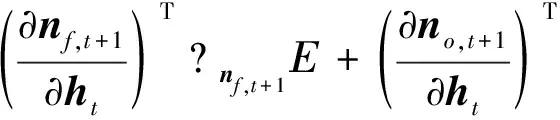
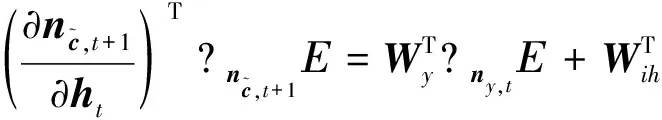

(11)
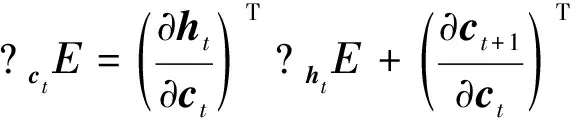
(12)
(13)
进而得到权重矩阵和偏置项的梯度分别为
(14)
(15)
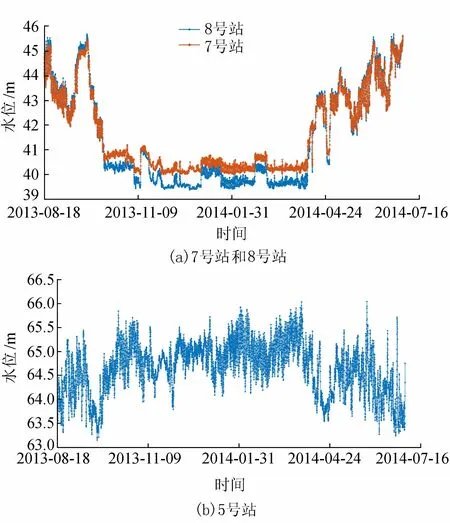
由以上梯度公式就可以采用梯度下降法来更新权重和偏置项。本文将梯度下降法和拟牛顿法中的BFGS算法相结合,在初始阶段误差比较大时,采用梯度下降法,当总误差减小到一定程度后,采用BFGS法来训练,并通过Wolfe-Powell线搜索来搜索合适的步长,提高迭代效率。设模型参数ω={Wfh,Wfx,Wih,Wix,Woh,Wox,Wch,Wcx,Wy,bf,bi,bo,bc,by},给定它的初始值ω0;精度阈值为ε;迭代次数为j;最大迭代次数为jmax;梯度下降法转为BFGS算法的阈值为a;D表示逆海森矩阵的近似,其初始矩阵设为D0=I,I表示单位矩阵。参数更新算法的具体步骤为:①计算模型训练的总误差E(ω),以及总误差对参数的梯度E(ω);②若E(ω)>a,则下降方向δω=-E(ω),根据线搜索得到步长α,更新参数ωnew=ω+αδω,转至步骤⑤,否则转至步骤③;③下降方向δω=D[-E(ω)],根据线搜索得到步长α,更新参数ωnew=ω+αδω;④若E(ω),则s=ωnew-ω,m=E(ωnew)-E(ω),h=Dm,k1=更新D,即Dnew=D+k2ssT-k1(shT+hsT);⑤若‖E(ω)‖>ε且j 选取2013年8月18日至2014年7月2日三峡水电站和葛洲坝水电站非弃水期间的小时运行数据,输入变量为三峡上游凤凰山水位、三峡左岸电站总有功、右岸电站总有功、地下电站总有功、电源电站总有功、葛洲坝大江电厂总有功、二江电厂总有功、自备电站总有功,输出变量为葛洲坝上游5号站水位、下游7号和8号站水位,训练前先将数据进行标准化处理,消除量纲的影响。图3(a)显示了7号站和8号站的水位走势,图3(b)显示了5号站的水位走势,图4为葛洲坝入库流量与5号站水位散点图(7、8号站散点图类似,不再画出),图5显示了三峡水库出库流量与葛洲坝入库流量之间关系。从图4可以看出,葛洲坝入库流量是葛洲坝上游5号站水位预测的重要影响因素,而葛洲坝入库流量又与三峡水库出库流量有着紧密的联系。从图5可以看出,三峡水库出库流量和葛洲坝入库流量呈宽带状分布,在相同的三峡水库出库流量水平下,葛洲坝入库流量有比较大的取值区间,仅仅采用线性回归来估计葛洲坝入库流量会产生较大的误差。另一方面,三峡和葛洲坝梯级电站的流量数据均是计算得到,本身含有一定的偏差,因此本文没有选取流量数据,而是通过水位和有功数据等实时监测数据来间接反映流量的隐含变化。 图3 不同站位水位走势 图4 葛洲坝入库流量与5号站水位散点图 图5 三峡水库出库流量与葛洲坝入库流量关系 由于三峡水库的出库流量到达葛洲坝坝前需要一定的时间,所以三峡水电站的水位和出力变化对葛洲坝水电站水位的影响存在一定的滞后性,当预测葛洲坝水电站上下游水位时,应综合之前多个时刻三峡水电站和葛洲坝水电站的出力情况以及三峡上游凤凰山的水位数据。本文采用LSTM神经网络,将历史每60个时刻的数据通过隐含状态引入到下6个时刻的预测之中,每个时刻的输入为8维,隐含层为20维,输出为3维,采用BPTT算法进行训练。为了评估模型的预测效果,采用预测误差的均值、标准差、平均绝对误差(YMAE)和均方根误差(YRMSE)作为评价指标,计算公式分别为 (16) (17) 表1 8号站连续6 h预测误差的统计结果 表3 5号站连续6 h预测误差的统计结果 从表1~表3可以看出,无论是上游5号站水位,还是下游8号站和7号站水位,误差结果分析的各项指标均随着预见期的延长而增大,说明预见期越长,水位越难以准确预测;对于8号站和7号站,其连续6 h的预测误差的90%分位区间基本在±0.2 m以内,而且YMAE和YRMSE值均较小,总体达到水位预测的精度要求;对于5号站,连续前3 h的预测误差的90%分位区间控制在±0.2 m以内,但是第4到6 h的YMAE值和YRMSE值均比较大,误差波动性较大,这主要是因为5号站处于三峡水电站和葛洲坝水电站之间,水动力学特性远远比下游河道复杂,所以对于5号站水位的预测,建议采取连续3 h预测,及时更新的方法来确保预测的有效性。 本文建立了基于LSTM神经网络的梯级电站短期水位预测模型。考虑上游电站的运行对下游电站水位的影响以及时间的滞后性,将上游电站的水位以及出力等可观测数据放入模型之中,并采用梯度下降法与拟牛顿算法中的BFGS方法相结合训练模型,Wolfe-Powell线搜索方法选取步长。将模型应用于葛洲坝水电站上下游水位预测,结果表明模型实现了葛洲坝水电站连续6 h的下游水位准确预测,以及连续3 h的上游水位准确预测,为科学的调度决策提供了更加可靠的理论支撑。2 葛洲坝水电站上下游水位预测
2.1 数据采集及分析
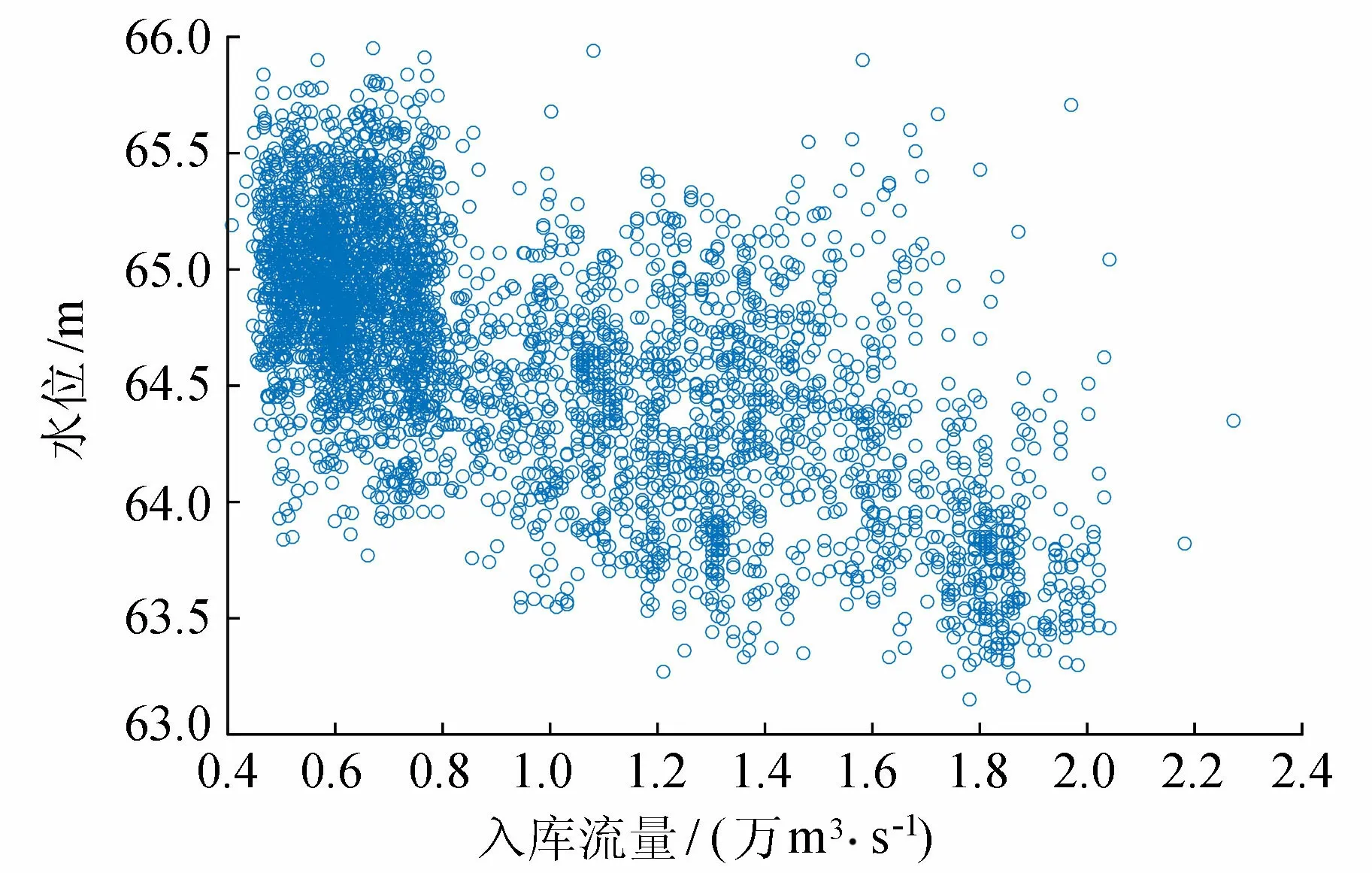
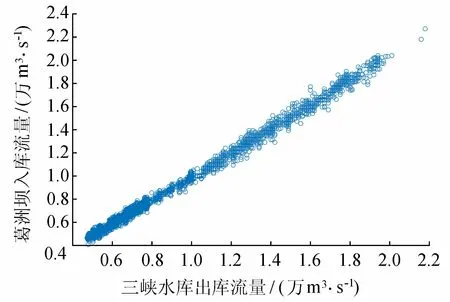
2.2 水位预测
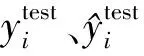
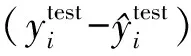
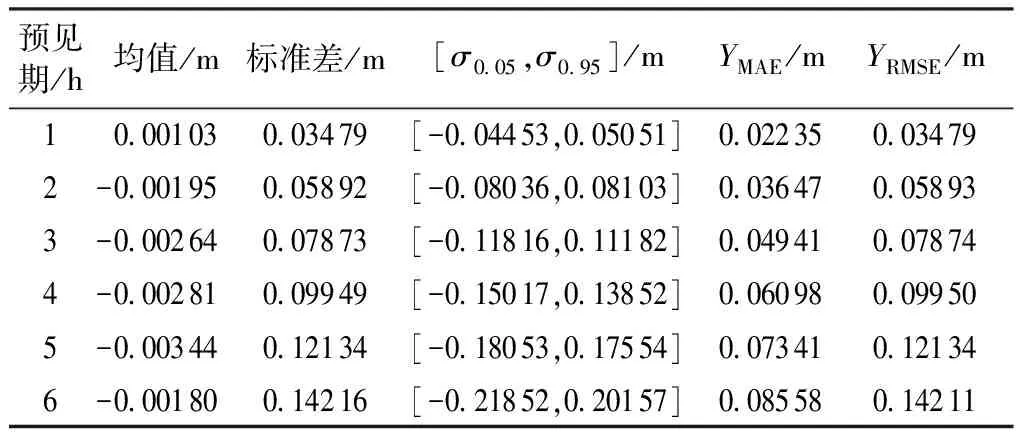
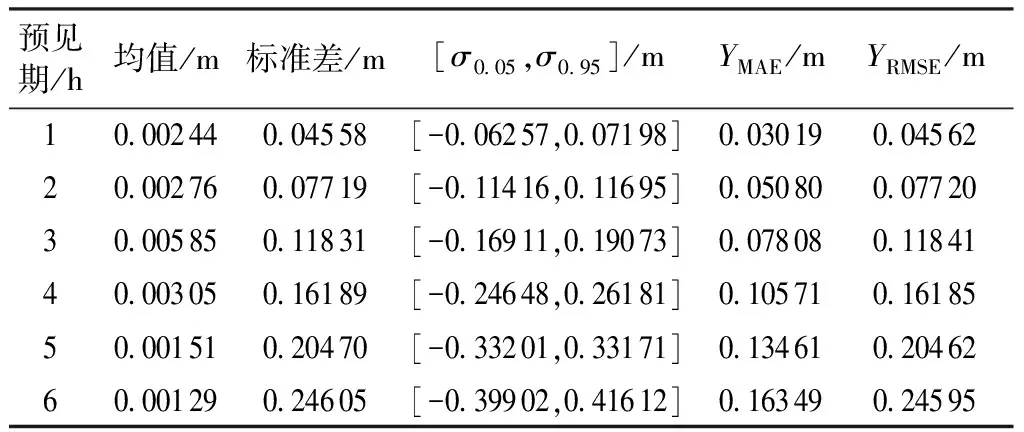
2.3 结果分析
3 结 语
