基于Haar小波与ARIMAX模型进行短期负荷预测

党亚峥，徐腾飞，高 岩

（上海理工大学 管理学院，上海 200093）

随着我国电力供给改革的进一步深化，电力供给方式出现多样化发展，其中，最具潜力的就是电力竞标，而电力竞标的依据之一就是短期负荷预测。短期负荷预测的精度直接影响到电网管理系统的规划、调度，甚至电网的安全性和运营能力，始终是电力系统研究的一个重点[1-2]。

由于电力负荷对天气、线路规划、政策以及电力系统运行等外部环境敏感，使得电力负荷预测的难度要比电力价格预测的高。但是，鉴于负荷与电价的高度相关性，许多用以预测电价的方法能在预测负荷方面使用[3-5]。较为流行的方法是将经典 ARIMA（auto regressive integrated moving average）预测模型[6]、神经网络法[7-8]与小波分析法[9]进行有机组合。采用经典ARIMA预测模型对已经进行小波降噪处理的电力负荷值进行预测，虽比单一使用ARIMA预测的精度高，但没有考虑到电价信息对电力负荷的潜在影响，将部分属于电价信息的因素作为噪声进行了消除[10-11]。采用神经网络（artificial neural network）预测方法对电力负荷进行小波变换后的序列值进行预测，但神经网络由于过度依赖人为调节阈值，使得环境的适应性较低[12-13]。其他研究都充分利用了小波分析在处理时间与频率信息、聚焦峰值与细节方面的优异性能，使得处理信息丢失少，这种对非平稳信号的处理能力会随着研究的深入而逐步增强[14-16]。

本文凭借小波分析适应非平稳信号程度高、对时域和频域的多尺度刻画精细等优点，充分利用ARIMAX模型对被解释变量滞后值的解释能力强的特性，加入电价信息序列，构建新的W-ARIMAX模型预测方案。

1 理论基础

1.1 小波分析

小波分析基于傅里叶变换，具有对局部分析能力强、非平稳序列拟合程度高、时频多、分辨率高的优点，且对环境的自适应度高，应用广泛[17-18]。小波定义：在能量有限的空间中，满足变换条件（式（1）），则称为小波。

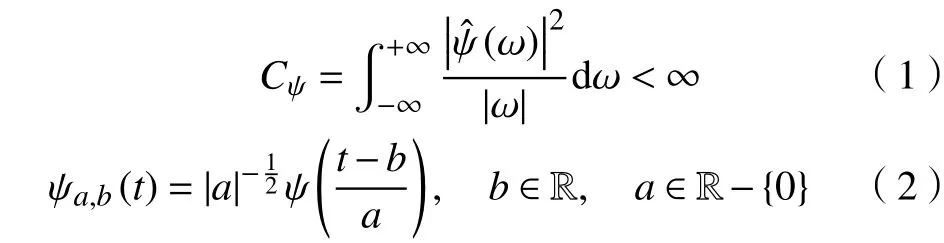
小波的逆变换

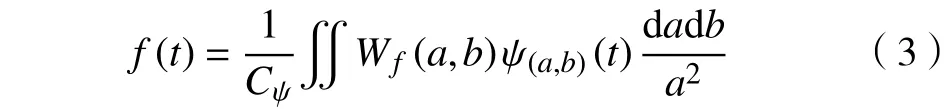
在对历史电价、负荷序列分解测试中，比较Mexico草帽小波、Daubechies法、Mallat法与Haar小波法，采用对数据平滑趋向拟合较好的方法，本文优选出Haar正交小波作为分解工具[19-20]。同时，由于每一层分解都会产生误差，分解层数越多，误差越大，预测精度也会越低。对电价的分解层数进行论证，分解一层为宜[21-22]，本文支持该论断。

1.2 ARIMAX模型理论

在随机序列中，对其单位根检验结果不能显著拒绝原假设，说明存在单位根，是非平稳序列。显然，电价与负荷均是非平稳的时间序列，电价与负荷序列在时间上有密切的正相关均衡关系，本文对历史电价与负荷进行整协检验，并未出现虚假回归问题，证实含有电价信息与负荷信息确实可以构成ARIMAX模型对负荷预测。

而ARIMAX模型的构成单元是ARIMA（ autoregressive integrated moving average model） 模型，且ARIMA经过差分d，平稳化处理后即为ARMA。ARMA模型为

式中：xt为序列值；是均值为0的随机干扰序列；与是时间序列xt的未知数参数；p为自回归阶数；q为移动平均阶数。

ARIMAX模型需要对参数p，d，q进行优选定参，主要方法是AIC法与BIC法[23]。AIC法是指提取观测值最大信息量后产生的下降至最小，以此定参数，但需要已知白噪声的概率分布，这种基于先验论的方法进行定阶就会出现偏误。理论已经证明，样本数量长度的无限变大，其计算值不会越来越接近真实值；BIC法是对前者的改进，强调模型高阶数与低阶数的影响权重，但因权重大小会引起区间震荡，在波动性很强的领域，如电价与负荷，单一采用BIC法会产生严重的偏离值。因此，本文首先采用AIC法约定数个阶数，再采用BIC法核定阶数，选出最优阶数用来预测负荷。

2 短期负荷预测的W-ARIMAX模型

2.1 W-ARIMAX模型思想

小波分析是对周期电价、负荷序列进行多频率的分解与重构，将电价、负荷的低频部分作为函数的近似，是概貌信息序列；将电价、负荷的高频部分作为函数的分量，是细节信息序列。从信号角度分析，将后者分离属于“降噪”过程。去噪后的电价、负荷概貌信息序列，采用ARIMAX模型可以大致预测出负荷的未来值，但是，由于初始信息被剥离一层，因此，需要细节信息序列来补充。这两者采用ARIMAX模型均是基于小波分析（wavelet analysis）为前提，故本文命名为“WARIMAX”模型。

W-ARIMAX预测方案：首先，将电力负荷与电力价格的混合模块信息带进行小波分解，得到时域的概貌信息序列与频域的细节信息序列；其次，对两者的概貌与细节分别进行协同ARIMAX模型预测，得出短期负荷概貌与细节的预测值；然后，将两组拥有电价信息的预测值进行小波重构，得出最终的短期负荷预测值；最后，运用本文构建的 W-ARIMAX模型对PJM（Pennsylvania New Jersey Maryland）公司的历史电力负荷值进行预测。建模过程中验证了对负荷和电价的最优小波分解层数是1，对多变量参数进行优化是必要的，负荷分解后进行单一预测会产生较大偏误。研究表明，W-ARIMAX模型预测方案可以提高短期负荷预测精度。

2.2 W-ARIMAX模型步骤与流程图

W-ARIMAX模型需要对非平稳的电价、负荷时间序列实施小波分解，然后以电价作为自变量，以负荷作为因变量，依靠历史数据进行短期负荷预测。其建模流程如图1所示。建模步骤：

a.对历史电价、负荷分别进行自相关（AIC）与偏自相关（PAC）检验，通过检验（证明两者不是白噪声序列）后进行下一步；

b.分别对历史电价、负荷序列进行二进制的正交Haar连续小波分解，得到两者的概貌信息序列与细节信息序列；

c.针对概貌信息序列，以历史电价为自变量、负荷为因变量套用ARIMAX模型，首先识别两者的相关性，然后优选AIC法与BIC法定阶数，建立回归预测模型，对残差序列进行单位根检验，并预测未来负荷的概貌信息序列；

d.对细节信息序列仍使用ARIMAX模型，预测未来负荷的细节信息序列；

e.将负荷的概貌信息序列与细节信息序列预测值作为小波重构，基函数仍为Haar小波。

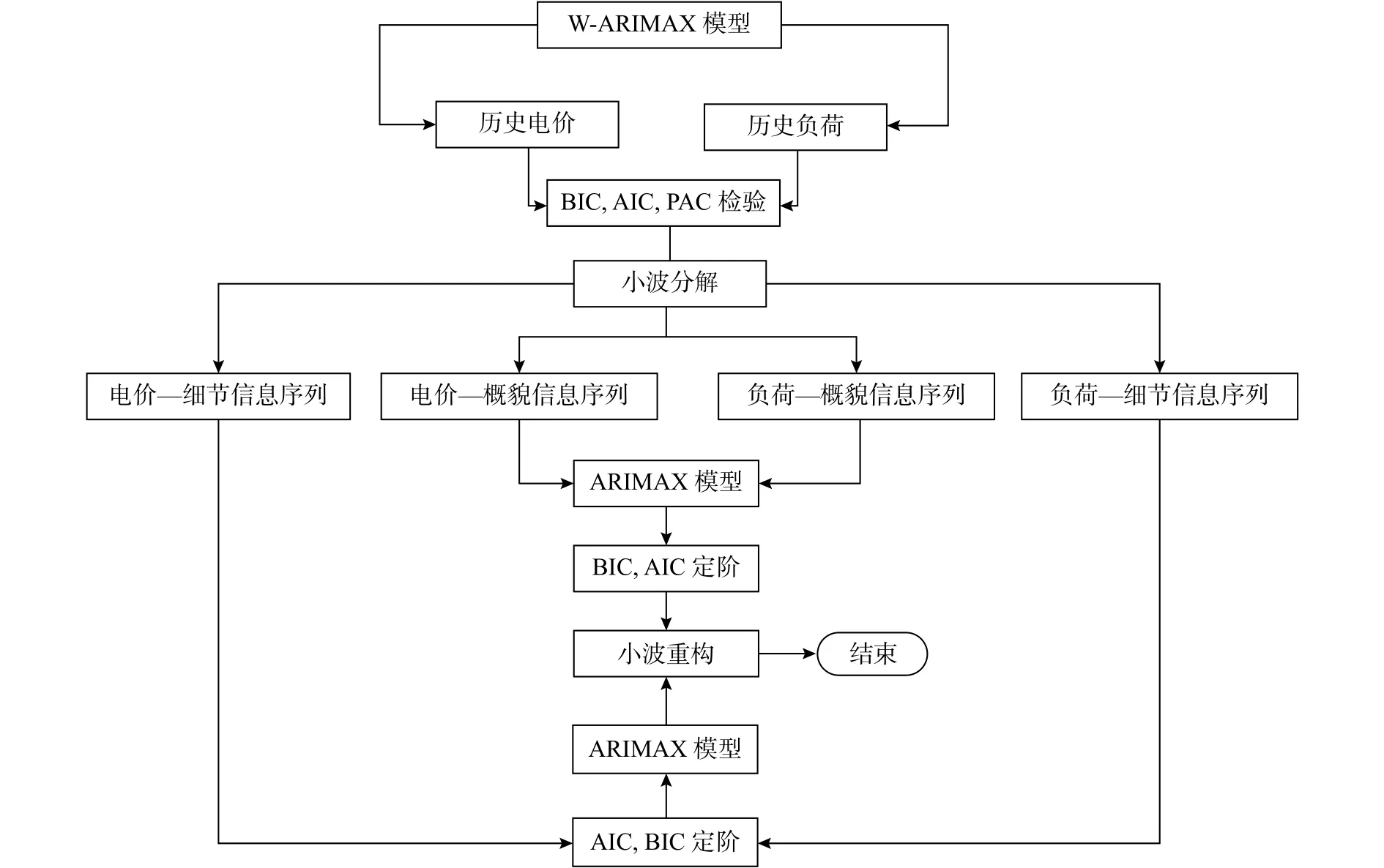
图1 W-ARIMAX模型流程Fig.1 Flow-process diagram of the W-ARIMAX model

3 算例证明

小波分析结合电价信息，构建的W-ARIMAX模型对负荷值进行预测，这一新的组合方法需要运用实例证明。本文采用美国联合PJM公司2017年1月的历史电价、负荷。由于电价与负荷的单位以及体量值不同，本文将负荷数值缩小109倍，处理后的数值将不再带有单位。数据可从官网下载，http://www.pjm.com/markets-andoperations/energy/real-time/monthlylmp.aspx，两者的时间序列如图2所示。t为时间，X为电价，Y为负荷。

图2 电价和负荷时间序列折线图Fig.2 Time series lines graph of the electricity price and load

首先，对历史电价与负荷的时间序列进行白噪声检验，结果表明，两者都有强的自相关和偏自相关，这是能对未来负荷进行预测的基础。然后，分别利用Mexico草帽小波、Daubechies法、Mallat法和Haar小波法进行分解与重构，分别将每种方法模拟效果最佳的序列进行比较，优选Haar小波。基于Haar小波对历史电价与负荷的时间序列进行分解，分别得到两者的概貌信息序列（aprox）与细节信息序列（detail），如图3和图4所示。

图3 电价与负荷的概貌序列折线图Fig.3 Low frequency sequence line graphs of the electricity price and load

对分解后的负荷概貌信息序列，加入电价概貌信息序列作为信息，构建为概貌信息序列的WARIMAX模型，并且对参数进行择优后，对未来3天的负荷概貌信息序列进行预测，得到概貌模型与预测时序图5。 概貌模型的差分为一阶差分，步长为 24，移动平均阶数q：1−0.403 94B（1），自回归阶数p：1− 1.886 12B（1）+ 1.279 62B（2）− 0.482 04B（3）+0.217 31B（4） − 0.213 56B（5）+ 0.067 31B（6）+0.110 31B（7）+ 0.075 29B（8）

其中，B(N)是指第N个参数。

对分解后的负荷细节信息序列，加入电价细节信息序列作为信息，构建为细节信息序列的WARIMAX模型，对参数进行择优后，对未来3天的负荷细节信息序列进行预测，得到细节模型与预测时序图6。细节模型的差分为一阶差分，步长为24，自回归阶数p为

1− 0.459 97B（1） + 0.259 61B（2） + 0.045 26B（3） +0.077 74B（4） + 0.042 07B（5） + 0.011 98B（6） +0.063 74B（7） + 0.109 27B（8） + 0.021 09B（9） +0.014 38B（10） + 0.079 54B（11） − 0.858 69B（12） +0.462 72B（13） − 0.218 72B（14） + 0.046 43B（15）

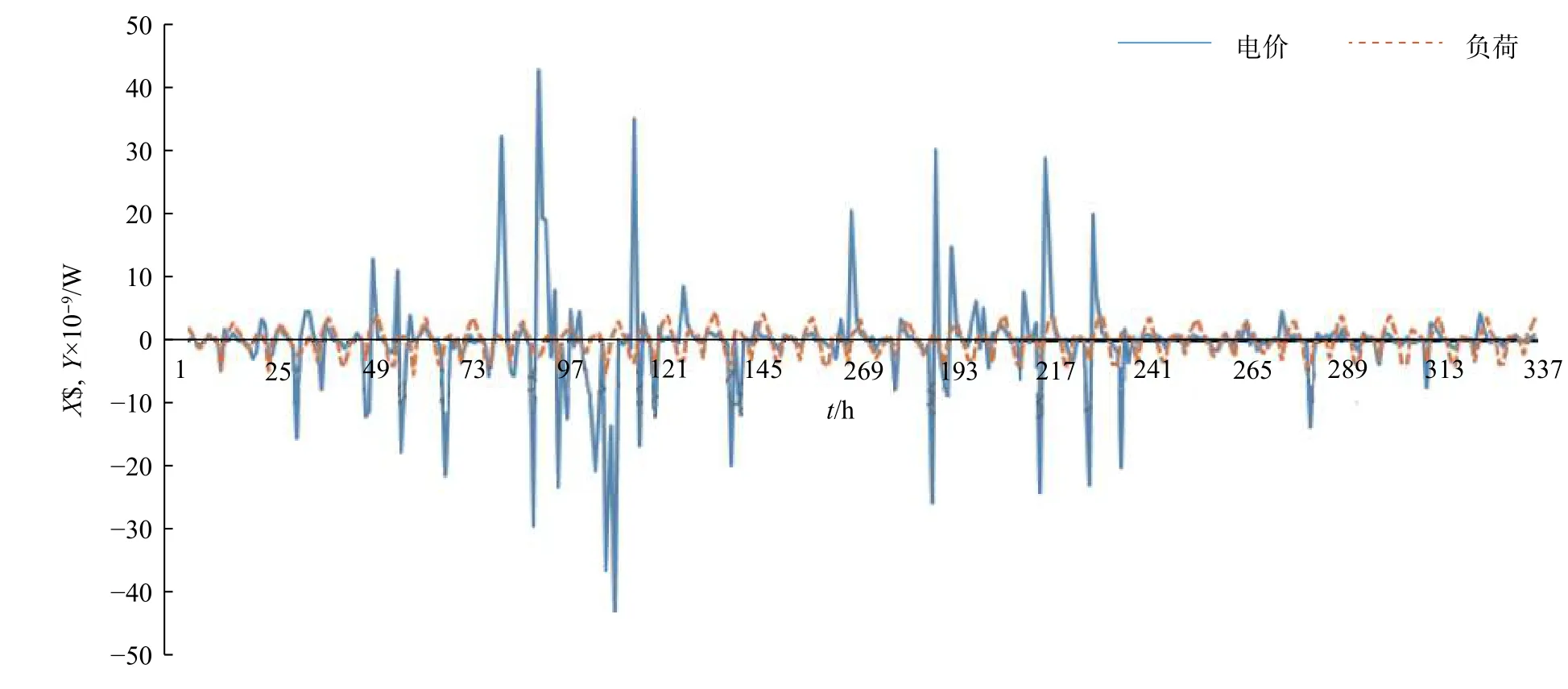
图4 电价与负荷的细节序列折线图Fig.4 High frequency sequence line graphs of the electricity price and load

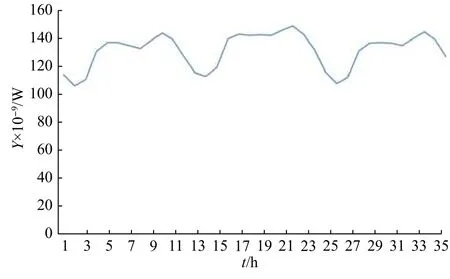
图5 概貌序列预测折线图Fig.5 Low frequency sequence forecast line graphs

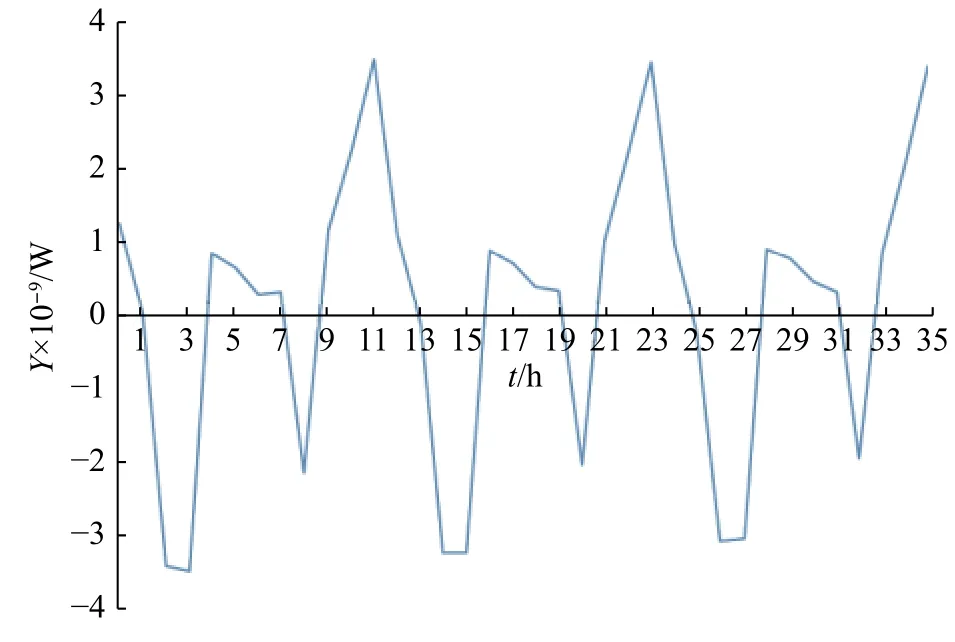
图6 细节序列预测折线图Fig.6 High frequency sequence forecast line graphs

为了进一步验证引入Haar小波分解对负荷预测效果的影响，本文构造了基于小波的ARIMA模型（WARIMA模型），对未来负荷概貌信息序列与负荷细节信息序列的预测值进行小波重构，得到未来3天的负荷预测值，将含有电价信息和小波分析ARIMAX模型的预测结果（W-ARIMAX）、不含有电价信息与小波分析的经典ARIMA模型的预测结果（ARIMA）、不含有电价信息（含有小波分析）的经典ARIMA模型的预测结果（W-ARIMA）同真实负荷值（Real）进行比对，如表1所示，并输出直观的3种模型预测时序同真实值的对比，如图7所示。

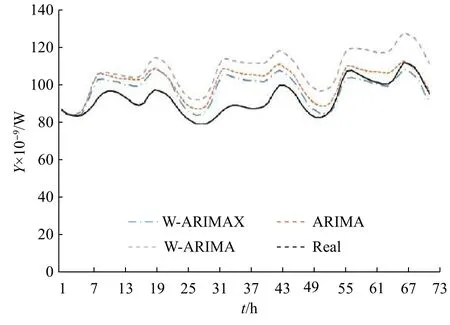
图7 3种模型的预测时序同真实值的对比图Fig.7 Comparison of the predicted time series by the three models with the real values

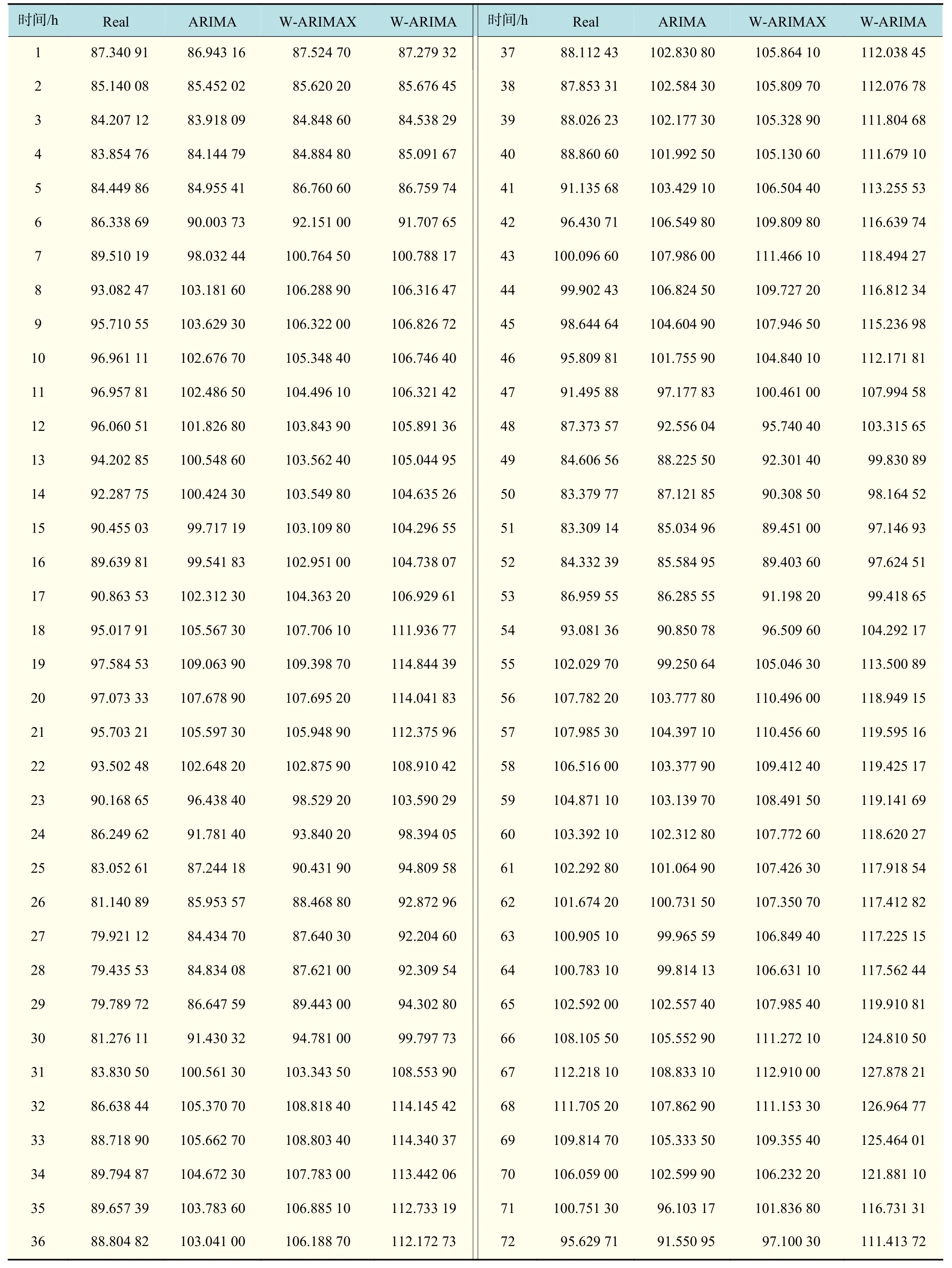
表1 3种预测方法输出值与真实值Tab.1 Output values of the three forecasting methods and real values

4 结 论

a.选用Haar小波作为小波分解的基，模型在定阶过程中，先采用AIC法定出p与q，并且比对BIC法定出的p与q，在有限的几组参数中选取最佳值，既提高了精确度，又节省了调参时间，预测效率明显提高。

b.在ARIMA 模型、W-ARIMA 模型、W-ARIMAX模型预测值对比过程中发现，构建的含有电价信息的W-ARIMAX模型，丰富了数据信息，弥补了两次误差序列丢失的信息，用该模型预测达到5.74%相对精度（7.1%绝对精度），比W-ARIMA模型的相对精度提高了3.59%（绝对精度提高了2.25%），更比经典ARIMA模型的相对精度提高了10.23%（绝对精度提高了8.88%）。

c.从3个模型的预测序列图中发现，在负荷趋势走向明显的情况下，新构建的W-ARIMAX模型的拟合效果好，但出现尖峰时就会出现预测值爬升与回荡乏力的情况，下一步工作需要构建合适的动量因子加以改善。