SMW工法基坑围护结构动力特性分析
2019-03-26钟传江
钟传江
(中铁十七局集团有限公司 山西太原 030006)
1 引言
在上海等软土地区,水泥土搅拌法和SMW工法作为基坑的围护结构得到了一定应用,但常规设计中往往只考虑静荷载的作用。由于许多基坑工程距离公路或铁路较近,各种动荷载具有不同的频率幅值变化和作用历时会引起水泥土围护结构的不同响应。所以,基坑围护结构的动力特性分析具有重要的实际意义。
基坑围护结构设计时会涉及到水泥土属性的确定问题。由于水泥土内部存在着大量初始缺陷,这些初始缺陷受荷后的发展变化直接影响着水泥土的宏观力学行为。充分认识切实把握疲劳荷载作用下水泥土内部损伤机制及其宏观力学响应特征,对正确评价动荷载作用下水泥土围护结构的使用效能、进行合理的水泥土围护结构抗疲劳设计,具有重要的理论意义及工程应用价值[1-4]。
低频循环荷载下水泥土的变形性态具有以下特征[5-6]:(1)对于同一组试样,不同应力水平下达到破坏的持续时间(循环周数)及变形速率不同;(2)循环应力作用下,变形速率随着循环周数会由大变小;(3)水泥土破坏具有局部扩展性质,破坏之前要经历一个疲劳损伤的累积过程;(4)水泥加固土在循环荷载下的变形特性明显地受到试验中的最大应力幅值的制约,应变速率明显地随着试验中的最大应力幅值的下降而降低。试验发现[5],当荷载振幅最大值为最大静载荷的80%时,水泥土往往只承受几周便崩塌;在45%~80%时,循环周数达到几千周到几万周不等;低于45%时,水泥土的动力性能明显地提高,往往循环几万周以上也不会破坏,其变形量仅为总控制变形量(5 mm)的25%,寿命急剧增长。水泥土在循环周数不大的情况下,试件大部分发生破裂,并有较明显的塑性变形,属于低循环疲劳(短寿命疲劳);水泥土在循环周数较大的情况下,试件在最终破坏之前整体上无可测的塑性变形,试件的疲劳寿命较长,属于高循环疲劳(长寿命疲劳)。一般认为,低循环疲劳在循环应力超出弹性极限时发生,高循环疲劳在循环应力低于弹性极限时发生。在循环荷载作用下,水泥土会在比峰值应力低的应力水平下,由于变形累加到一定程度而导致破坏,表现为低应力性破裂特征。水泥土疲劳失效的过程可分为3个主要阶段:疲劳裂纹形成、疲劳裂纹扩展及当裂纹扩展达到临界尺度时,微裂纹相互联接而破裂。荷载振幅与荷载频率直接影响着水泥加固土的疲劳寿命,且荷载振幅的影响比荷载频率对疲劳寿命的影响要大得多。水泥加固土在循环荷载下的变形特性明显地受到最大应力幅值的制约(应力幅值最大值为无侧限抗压强度试验中最大载荷的70%~80%)。
本文拟根据SMW工法基坑围护结构工程案例,在建立三维有限元模型的基础上,研究不同支撑条件下基坑围护结构的动力特性。
2 SMW工法单桩的动力特性
2.1 人为地面振动传播简介
对铁路和城市轨道交通等引起的环境振动,国外从20世纪80年代起陆续开展研究,特别是对快速列车和重载列车引起的地面振动及其对周围环境的影响进行了研究,提出了一些计算方法和计算模型[7-10]。日本是受环境振动污染最为严重的国家之一,对交通车辆引起结构振动的机理、振波在地下及地面的传播规律及对周围居民的影响进行了研究,提出了环境振动水平的预测方法。英国建立了分析高速列车引起地面振动放大的计算模型,认为当列车速度超过地面Rayleigh波速(如列车车速达到200 km/h)时就可能发生地面振动放大现象。瑞士对地铁列车和隧道结构的振动频率和加速度特征进行了研究,从改善线路结构的角度提出了降低地铁列车振动对附近地下及地面结构影响的途径。挪威学者进行了软弱场地上高速列车的测试,认为当列车车速接近某一临近值(地面特征波速),钢轨-路基-地面系统的动力响应将会出现较大的动力放大[11-13]。
Eiichi等的研究表明:位于地下2 m深处的振动加速度为地面的20%~50%;4 m深时,这一比例减小到10%以下。换言之,车辆运行产生的环境振动中,表面波为主要成分的波。如果地面振动由地铁或隧道中的列车引起,其振源能量仅以体波形式传递到地面。
因此,随列车速度的提高,高速列车引起的噪声和地面振动水平显著增加,这些振动产生的波若与施工中的围护结构有较近的固有频率,将引起围护结构共振等动态响应。
2.2 动力面源引起的地面波动的衰减计算
动力面源传给地基土介质的能量,是体波(P、S波)与面波(R波)的组合,这两种波叠加起来,可得距波源中心r处自由地面的振幅:

式中,r为距动力面源中心的距离;Ar为距动力面源中心r处地面振幅;f0为波源扰动频率(已测资料在50 Hz以内);A0为波源振幅;ξ0为与波源面积有关的几何衰减系数;a0为地基土能量吸收系数;r0为波源半径。对于矩形或正方形面积,当量半径为:

式中,F为波源面积;μ1为动力影响系数。F≤10 m2时 μ1=1.00;F≥10 m2时 μ1=0.80。
式(1)中根号数值反映了波能量密度随着与波源距离的增加而减少(即为几何衰减),根号外指数项表示波的消耗。波源半径r0较小时,ξ0值较大,即体波所占成分大;r0值较大时,ξ0值趋向小,即体波所占成分较小,面波成分相应提高。
波源半径可按规范选取:铁路部门取r0=3.0 m;道路部门取r0=3.25 m(柔性路面)或r0=3.09(刚性路面)。
2.3 结构模态分析
结构模态分析就是确定结构的固有频率和振型,模态分析是其它更详细动力学分析的起点。本节中的模态分析是线性分析,非线性特性不予考虑。
研究时采用以下的模态分析步骤:(1)建立有限元模型;(2)施加载荷并求解;(3)扩展模态;(4)检查计算结果。
2.4 单桩模态分析模型
选取含型钢的单根SMW工法桩作为研究对象,建立相应的单桩模态分析模型(见图1)。将水泥土简化成矩形,H型钢型号为700×300,壁厚20 mm。模型整体长度18 m、宽度0.7 m、高度1.2 m。
模型中水泥土与H型钢均按弹性材料考虑,H型钢与水泥土之间设置接触单元,用以模拟二者之间的相互作用。
边界条件中,模型底面三向固定,左右两个面固定其法线方向位移,上下两个面作为实际工程中与土体的接触面。同时,假定“下面”与基坑内土体相接触,并与支撑相接,相接处限制法线方向位移(相当于在支撑位置加了法线方向的约束),具体位置为z=-1、-4、-7 m。z为桩端标高(桩顶端标高设为0)。

图1 SMW工法单桩模态分析模型
模型选用分块兰索斯法模态提取方法,定义提取前5阶模态,质量矩阵形成方式使用一致质量矩阵,不考虑预应力效应。
2.5 单桩固有频率和振型
通过模拟计算,得到SMW工法单桩前5阶模态的固有频率(见表1)。模拟得到前5阶模态下的单桩变形图见图2。
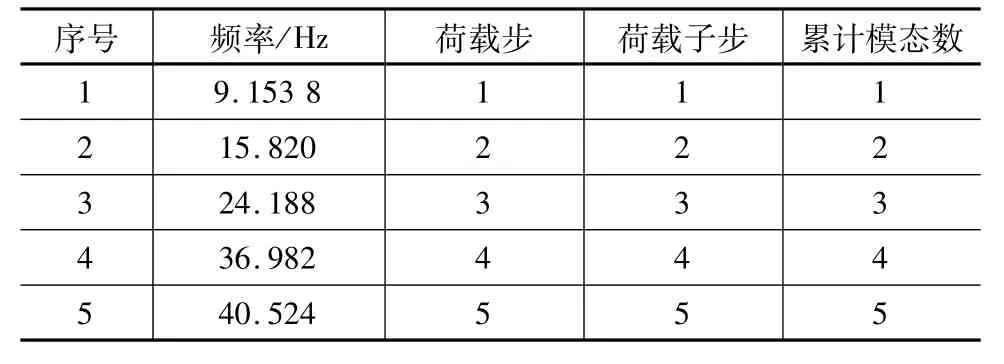
表1 SMW工法单桩的前5阶模态固有频率
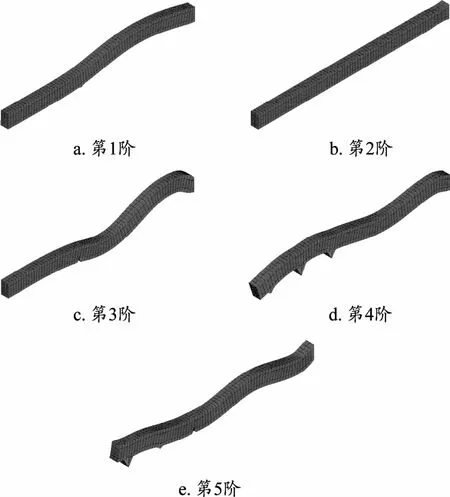
图2 SMW工法单桩前5阶模态变形
图2中,因为在支撑与SMW工法桩相接点z=-1 m、z=-4 m、z=-7 m处设置了约束,所以桩中出现一定的凸起或凹口。当撤销支撑位置处的约束(即考虑两列支撑间SMW工法单桩模态分析)时,得到固有频率(见表2)。

表2 撤销支撑约束后的单桩固有频率
进而得到撤销支撑约束后前5阶模态变形图,见图3。
由图2、图3可知,接有支撑的单桩固有频率比较大,振型也比较明显,在固有频率9.153 8、15.820附近,单桩变形相对较小;在固有频率 24.188、36.982、40.524附近,单桩变形相对较大。不接有支撑的单桩固有频率比较小,在固有频率0.537 81、4.402 4、15.820附近,单桩变形相对较小;在固有频率12.786、24.228附近,单桩变形相对较大。不论是否接有支撑,单桩在固有频率15.820时,变形都比较小。这说明,对单桩来讲,如果外加动荷载的振动频率在15.820附近时,变形最小,处于最安全的状态。
3 SMW工法围护结构的动力特性
3.1 围护结构模态分析模型
选取SMW工法整体围护结构作为研究对象,建立模态分析模型(见图4)。考虑到整体SMW工法围护结构建立真实形状比较困难,将H型钢与水泥土通过等效代换,只分析整个围护结构的模态,水泥土、支撑与H型钢均按弹性材料考虑。
围护结构底部三向固定,支撑直接与围护结构相接,具体位置为z=-1、-4、-7 m(z是围护结构的竖向标高,围护结构顶端标高设为0)。

图4 SMW工法整体围护结构模态分析模型
3.2 围护结构的固有频率和振型
模拟计算后得到前5阶的模态变形图见图5。

图5 SMW工法围护结构整体模态变形
图5中,围护结构内部设置了支撑单元。由于支撑刚度远小于围护结构的整体刚度,所以,围护结构的振型不明显;在不同的固有频率下,支撑变形都比较明显。这说明,在动荷载作用下,支撑很容易失稳,进而造成整个围护体系的破坏,直至基坑坍塌。
不考虑支撑时,可删除支撑单元,在支撑位置施加相应约束,从而建立了新的围护结构模态分析模型。重新计算后,得到SMW工法围护结构的前5阶模态固有频率,见表3。
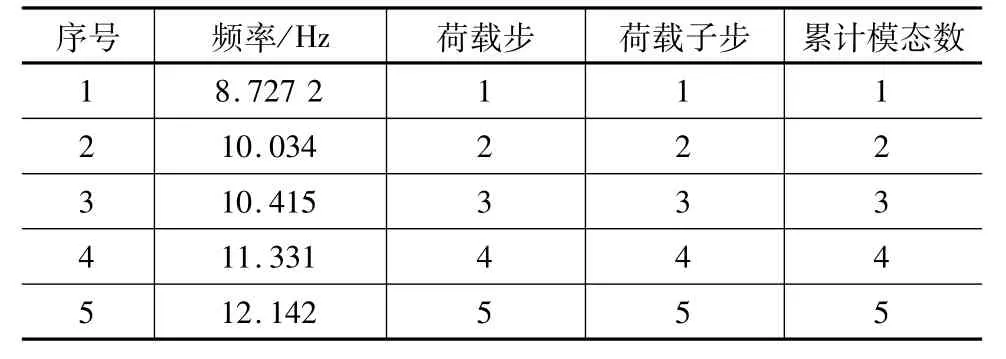
表3 撤销支撑位置约束后的围护结构整体固有频率
模拟得到撤销支撑位置约束后围护结构整体的前5阶模态变形图见图6。

图6 撤销支撑位置约束后的围护结构整体模态变形
SMW工法围护结构的前5阶固有频率主要为8.5 Hz~12.5 Hz,离散性不强,这与SMW工法单桩的固有频率不同。围护结构整体的空间效应是促成这种结果的主要原因。由图6可以发现,大的变形多发生在围护结构两头,拐角处不容易发生显著变形,这与围护结构的“L”形状相关。
4 结束语
(1)接有支撑的单桩最大固有频率比不接有支撑的单桩固有频率要大,固有频率的离散性更明显。另外,不论是否接有支撑,单桩在固有频率15.820 Hz时,变形都比较小。
(2)在不同的固有频率下,围护体系中支撑系统变形都比较明显。在动荷载作用下,支撑系统首先会发生破坏。
(3)与SMW工法单桩的固有频率不同,SMW工法围护结构的固有频率比较集中、离散性不强,围护结构整体的空间效应是促成这种结果的主要原因。
(4)大的变形多发生在围护结构两头,拐角处不容易发生显著变形,这与围护结构的“L”形状相关。
