非对称单侧悬臂施工斜拉桥结构参数敏感性研究

俞文龙 朱 飞 张胜雷

（1.中铁十七局集团有限公司 山西太原 030006；2.中铁十七局集团上海轨道交通工程有限公司 上海 200135）

1 引言

施工监控是保证桥梁实现设计意图并确保施工安全的重要途径［1-2］。在斜拉桥施工中，施工工序较多、施工程序复杂，结构影响参数也较多［3-4］。设计阶段，这些结构影响参数多按规范或理论计算进行取值，但在实际施工过程中由于实际控制水平以及人为、材料等因素的影响，参数实测值与规范、理论值之间会存在一定的偏差［5］。此偏差将会引起桥梁结构实际受力状态与设计状态之间的差异。因此有必要对结构影响参数进行分析，找出敏感性参数。对于敏感性参数则需要通过正确地识别和修正，减小计算值与实际值之间的偏差；对于非敏感性参数，修正的范围可适当放宽。敏感参数的合理取值与修正，不仅关系到桥梁的顺利合龙，也关系到成桥的内力状态和成桥线形，更关系到桥梁的施工安全［6-7］。

同时，斜拉桥施工方法的不同也将影响成桥时的结构内力以及主梁线形［8］。目前常规的混凝土斜拉桥施工方法是挂篮对称悬臂浇筑，而本文研究的背景工程斜拉桥为非对称结构，主跨侧施工为挂篮悬臂浇筑，而边跨侧为支架现浇。对本桥梁结构进行参数敏感性分析，目的就是为了确定出对桥梁施工及结构受力影响较大的几个主要参数，据此为桥梁施工监控提供理论依据［9］。

2 工程概况

苏州长浒大桥CA辅道桥为非对称、单塔单索面预应力混凝土斜拉桥，主桥跨径布置为104 m＋75 m，主桥全长179 m，标准桥宽19 m。主桥采用刚构体系，墩塔梁固接。斜拉索采用扇形索面，梁上标准索距为7 m，边跨加密段为3.5 m；塔上索距为1.8 m，全桥共24对斜拉索。主梁为单箱双室斜腹板箱梁截面，中心线处梁高2.1 m，顶板宽19 m，底板宽8 m，翼缘板悬臂长度为3.5 m，箱梁顶板设1.5%的单向横坡，底板水平。桥梁0#段长28 m，采用支架法现浇。跨运河侧主跨采用前支点复合式牵索挂篮悬浇，分为标准节段、合龙段和支架现浇段，其中挂篮浇筑标准段每节长度为7 m，共11节段，编号分别为1#～11#节段，主跨现浇段长11 m，主跨合龙段长2 m。边跨采用支架法现浇，与主梁0#段同步浇筑完成。由于斜拉桥设计为非对称结构，为保证斜拉索拉力均衡以使主塔不承受过大的水平荷载，设计在边跨侧设有永久填充铁块。填充铁块布置在边跨5#斜拉索向外的箱室内，除最外侧两节箱室，各节箱室填充铁块荷载重94.5 t，最外侧两节箱室填充铁块荷载分别为98 t和110.3 t。具体桥梁布置及节段划分如图1所示。

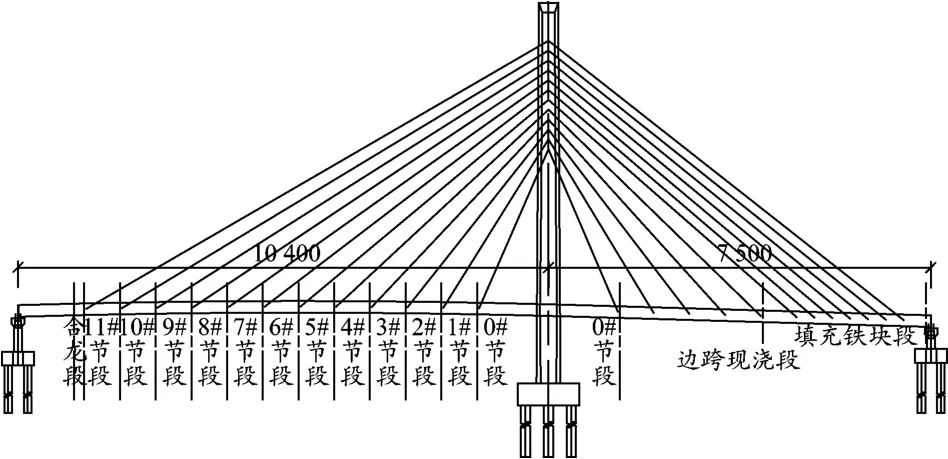
图1 长浒大桥主桥总体布置（单位：cm）

3 结构影响参数分析

桥梁结构影响参数分析就是要确定出对桥梁施工及受力影响较大的设计参数，此参数即为敏感参数，影响相对较小的为非敏感参数［10］。而如何判断各参数对桥梁受力状态的影响，需要确定具体控制目标。对于斜拉桥，最主要的目标状态就是成桥状态和最大悬臂状态。成桥状态为桥梁施工的最终状态，是施工过程控制的目的，控制好此状态即可顺利地完成设计意图；最大悬臂状态往往是桥梁施工过程中受力最不利的状态，控制好此状态，基本可以保证桥梁施工安全。因此本文分析各参数敏感性时确定的控制目标为：

（1）成桥状态：成桥主梁线形、成桥主梁顶底面应力和成桥索力。

（2）最大悬臂状态：最大悬臂端竖向位移、主梁根部顶底面应力。

根据背景工程桥梁的具体特点，拟分析的桥梁设计参数包括：主梁混凝土容重、混凝土弹性模量、斜拉索弹性模量、斜拉索初张力、主梁预应力荷载、施工临时荷载以及边跨填充铁块荷载。

3.1 参数敏感性分析

参数敏感性分析可采用的方法为：将拟分析的设计参数增大一定的幅值（此处取增大10%），其他设计参数不变，将成桥主梁线形、成桥主梁顶底面应力和成桥索力作为控制目标。对不同设计参数进行分别计算，根据计算所得的控制目标值随设计参数变化的程度可以确定出敏感参数。

计算得出成桥状态各控制目标随各设计参数的变化如图2～图5所示。图中横坐标X表示主梁纵向里程，以主塔位置为坐标零点，主跨侧为负里程，边跨侧为正里程；横坐标索编号正值代表边跨侧斜拉索编号，负值代表主跨侧斜拉索编号。

根据各计算结果分析得出：对成桥主梁线形影响较大的设计参数分别为斜拉索初拉力、主梁混凝土容重和斜拉索弹性模量，而其他几个设计参数对主梁成桥线形影响相对较小；对于成桥索力影响较大的设计参数分别为主梁混凝土容重、斜拉索初拉力、铁块荷载和预应力荷载，其他几个设计参数对成桥索力影响较小；对于成桥主梁顶底面应力，影响较大的参数分别为斜拉索初拉力、主梁混凝土容重、主梁预应力荷载和施工临时荷载，其他参数对主梁成桥顶底面应力影响相对较小。综合判断，斜拉索初拉力和主梁混凝土容重对成桥状态的几个控制目标都有较大的影响，可确定为敏感参数；其余参数或是对某个控制目标影响较大，或是对各控制目标影响都相对较小，可判断为非敏感参数。

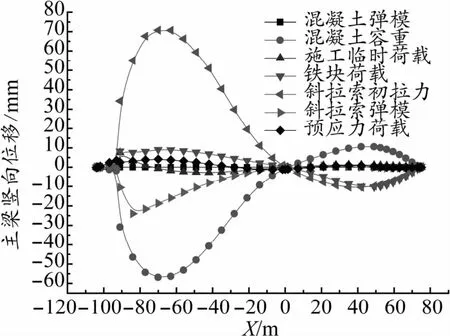
图2 设计参数增加10%引起的主梁竖向位移变化曲线

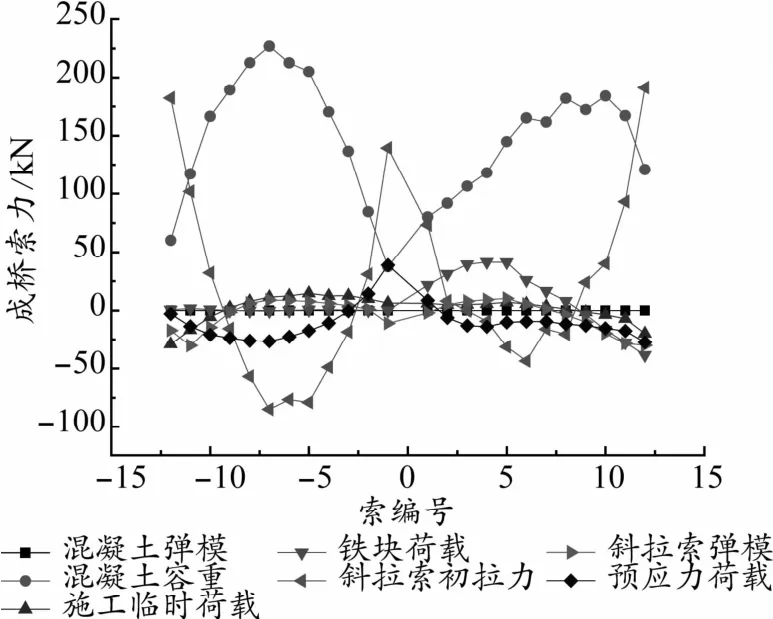
图3 设计参数增加10%引起的成桥索力变化曲线

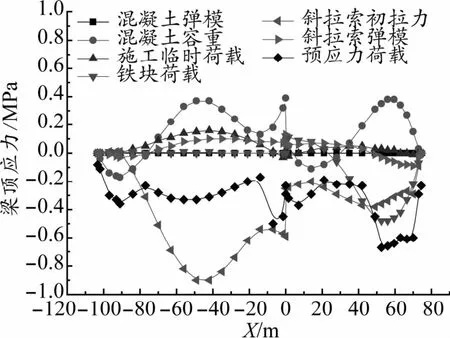
图4 设计参数增加10%引起的主梁顶面应力变化曲线

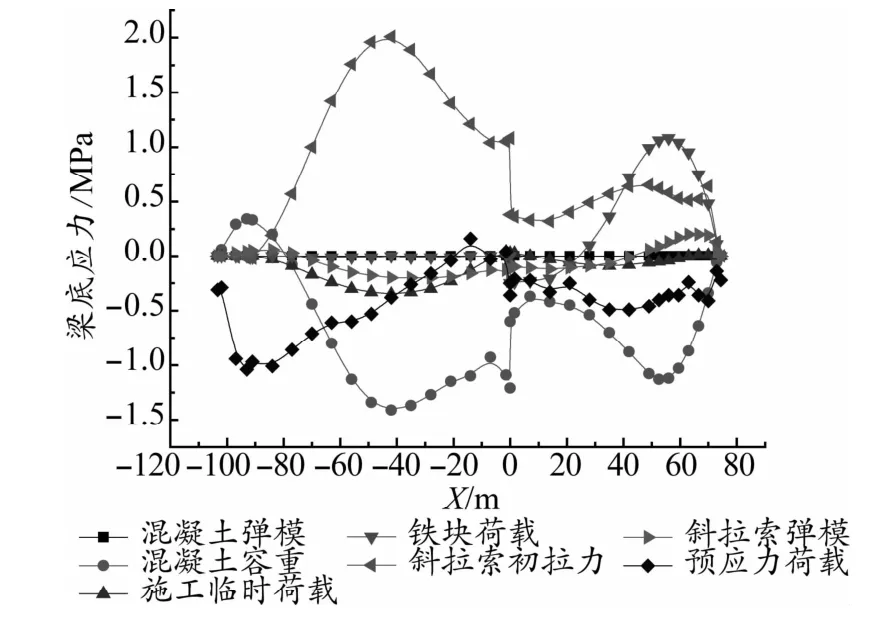
图5 设计参数增加10%引起的主梁底面应力变化曲线

3.2 敏感度计算

以上分析方法可直观地对比出各参数对控制目标的影响程度大小，并初步判断出敏感参数和非敏感参数，但对控制目标的影响程度没有给出量化指标。为更好地判断各参数变化对控制目标影响的敏感性，以参数敏感度为具体指标［11］，对比分析设计参数敏感性。

参数敏感度计算原理为：仅对某一设计参数进行数值调整，其他设计参数不变，借以考量该设计参数的相对影响因子［12］。具体分析方法为：将最大悬臂状态主梁悬臂端竖向位移和主梁根部顶底面应力作为控制目标，将各设计参数分别调整-6%、-3%、0、＋3%、＋6%，计算出不同调整率下的控制目标值。参数调整率与控制目标变化值之间的关系如图6～图8所示。从图中可以看出控制目标变化值与参数调整率之间基本都呈线性关系，控制目标变化值与参数调整率组成的关系曲线斜率即可被定义为相应控制目标随对应参数变化的敏感度。此敏感度的大小直接反映出设计参数变化对控制目标的影响程度，敏感度数值越大表示参数变化对控制目标的影响越大，敏感度值为正表示控制目标与设计参数之间呈正比例变化关系，敏感度值为负表示控制目标与设计参数之间呈反比例变化关系。根据以上计算方法，计算得出不同设计参数相对于控制目标的敏感度数值如表1所示。

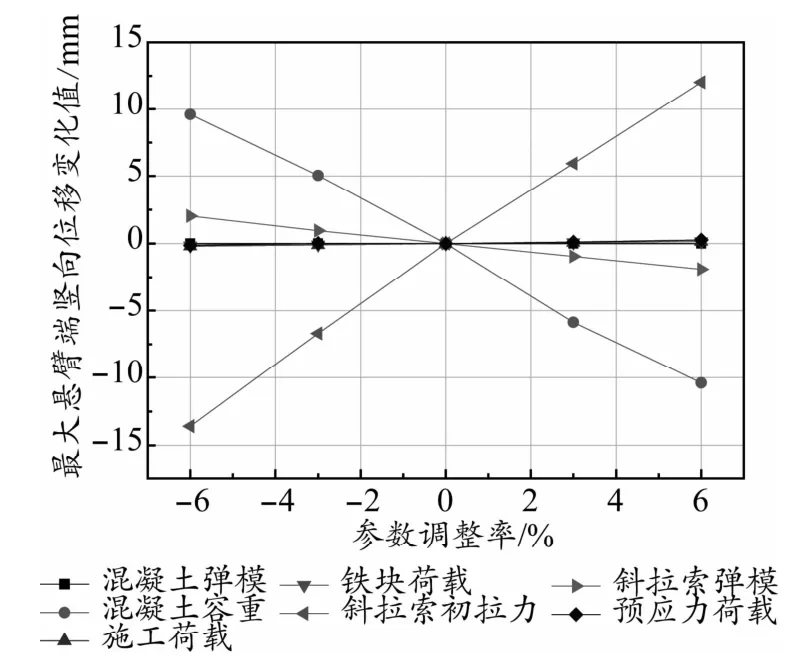
图6 最大悬臂端挠度与各参数调整率关系曲线

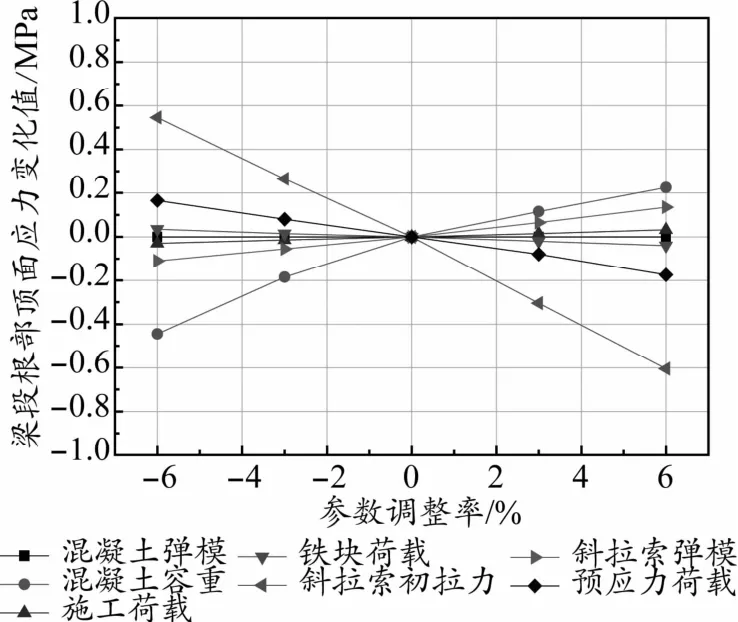
图7 梁段根部顶面应力与各参数调整率关系曲线

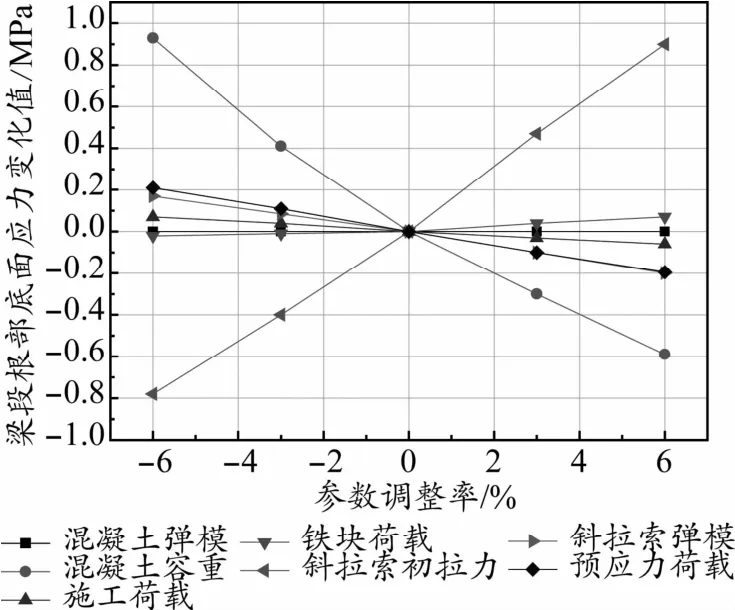
图8 梁段根部底面应力与各参数调整率关系曲线

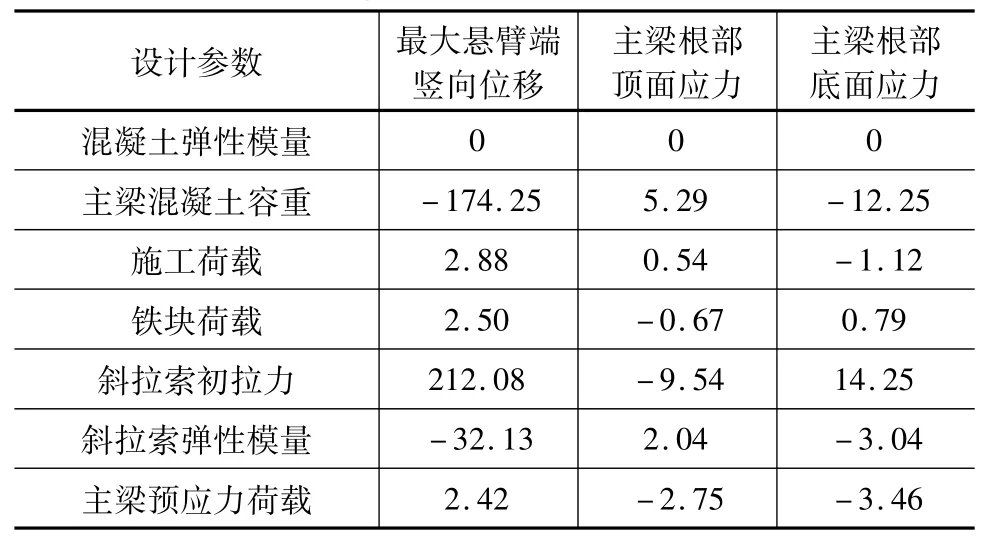
表1 不同设计参数相对于控制目标的敏感度值

从表1计算得出的敏感度值可以判断，本桥最大悬臂施工状态工况下，对主梁悬臂端竖向位移影响较大的设计参数依次为斜拉索初拉力、主梁混凝土容重和斜拉索弹模，此三个参数可判断为主梁悬臂端竖向位移敏感参数，其余参数对主梁悬臂端竖向位移影响敏感度值较小，可判定为非敏感参数。对于主梁根部顶面应力影响较大的设计参数依次为斜拉索初拉力和主梁混凝土容重，此两个参数可判断为主梁根部顶面应力的敏感参数，其余参数可判定为主梁根部顶面应力的非敏感参数。对于主梁根部底面应力影响较大的设计参数依次为斜拉索初拉力、主梁混凝土容重、主梁预应力荷载和斜拉索弹模，此四个参数可判断为主梁根部底面应力的敏感参数，其余参数可判定为主梁根部底面应力的非敏感参数。

综合以上三个不同控制目标的不同参数敏感度数值，可认为对本斜拉桥最大悬臂状态影响较大的设计参数为斜拉索初拉力和主梁混凝土容重，其余参数或是对某些控制目标影响稍大，或是对所有控制目标影响都较小，可判断为非敏感参数。

4 结论

（1）以成桥状态主梁线形、主梁顶底面应力以及成桥索力为控制目标，将各结构影响参数增大10%的幅值，得出敏感参数为斜拉索初拉力和主梁混凝土容重，其余参数可确定为非敏感参数。

（2）以最大悬臂状态最大悬臂端竖向变形和主梁根部顶底面应力为控制目标，以参数敏感度为指标，分析得出此状态下敏感参数为斜拉索初拉力和主梁混凝土容重，其余参数可判断为非敏感参数。

（3）以成桥状态和最大悬臂状态分析得出的桥梁敏感性参数结论基本一致，以参数敏感度为指标可以量化判断参数敏感性，建议具体分析时采用此类方法。