基于最大团的社交网络个性化推荐∗

陈小礼 汪 洋 彭艳兵

（1.南京烽火软件科技有限公司 南京 210019）（2.武汉邮电科学研究院 武汉 430074）

1 引言

个性化推荐是指考虑当前观众（网站，电视频道或任何其他内容）的优越用户体验，并根据系统对这些人的了解情况升级默认外观、感觉和内容，并作出相应推荐。个性化推荐虽然利用了推荐算法，但它更加专注于用户本身。随着现代计算机的出现，虽然互联网使得各种信息获取变得轻而易举，但信息的信息过载问题会使人们被太多选择淹没而犹豫不决［1］。为了解决以上的众多问题，传统上人们使用协同过滤推荐来进行推荐［2］。大多数协作过滤系统应用所谓的基于邻域的技术。在基于邻域的方法中，基于与活动用户的相似性来选择多个用户，通过计算所选择的用户的评级的加权平均值来进行活动用户的预测。协同过滤算法的优点很多，主要体现在对推荐系统的项目无过于苛刻的要求，并且在面对复杂的非结构化项目时处理起来相当方便。但由于新用户往往缺少有效的用户购物行为数据，很难对其进行推荐，这便是推荐系统中著名的冷启动问题［3］。

传统的推荐系统没有考虑到明确的用户之间的关系，但社会影响力在产品市场中的重要性却越来越大。此外，社会网络的整合理论上可以提高目前推荐系统的性能。首先，就预测获取的用户及其朋友的附加信息，社交网络提高了用户行为和评级的理解能力。因此，我们可以更准确地对用户偏好进行建模和解释，最终提高预测精度。其次，由于社交网络中存储着好友的相关信息，这会无需再测量他们的相似度，因为两个人是朋友的事实已经表明了他们有共同之处。因此，可以减轻数据稀疏问题。同时以社交关系为基础的社团和数据流是大多数用户所需要的［4］。实际上，许多用户行为是由多个用户以团队的形式参与的。将推荐的对象由某些单个个体拓展到一个团体，这样的推荐系统被人们称之为团推荐系统（group recommender system）［5］。在朋友推荐和系统推荐之间做出选择时，无论从推荐的质量还是推荐的有效性来看，用户往往更倾向于前者，所以提取和量化高质量的社交关系是改善推荐质量的法宝［6］。

本文针对传统的协同过滤都只能为单个用户进行推荐、用户项目推荐覆盖率小、存在冷启动的问题，提出了一种以社交网络为基础的最大团推荐算法。在YELP的数据集上的实验结果表明根据团体推荐即提高了推荐的准确率，也缓解了推荐系统的冷启动。

2 基本定义及算法描述

2.1 基本定义

定义1最大团问题，Maximum Clique Problem，MCP）：团就是最大完全子图。给定一组顶点，其中一些顶点之间有边缘，最大组是顶点的最大子集，其中每个点都直接连接到子集中的每个其他顶点。每次添加一个新点时，必须搜索的总群数至少增加一倍；因此我们有一个呈指数增长的问题［7］。

定义2协同过滤算法（Collaborative Filtering Recommendation，CF）：也被称为社交过滤，通过利用其他人的建议信息来给出当前用户的推荐信息。这是基于这样的想法，即在过去对某些项目进行评估的同意者可能会再次同意。一个想要看电影的人可能会要求朋友推荐。有些类似兴趣的朋友的建议比其他人的建议更受信任。该信息用于决定哪部电影可以看到。

定义3团预测评分［8］。群组G对项目i的预测评分groupprerating（G，i）由群组中每个用户预测评分prerating（u，i）融合得到。本文采用均值策略进行偏好融合时的群组预测评分计算方法：

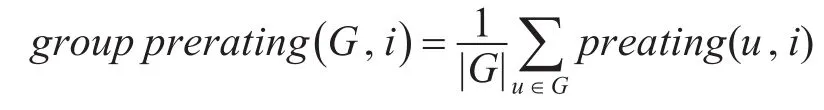
定义4最大独立集（Maximum Independent Set，MIS）［9］：从顶点集中任意选取N个顶点，这N个顶点两两间并无直接连线。

2.2 算法描述

协同过滤算法是基于在过去对某些项目进行评估的同意者可能会再次同意的想法。一个想要看电影的人可能会要求朋友推荐。有些类似兴趣的朋友的建议比其他人的建议更受信任。该信息用于决定哪部电影可以看到。不是只依靠最相似的人，而是预测通常是基于几个人的推荐加权平均数。一个人的评分的预测由该人与预测人之间的相关性决定［10］。相关度可以由式（1）（Jaccard index）亦或者式（2）（cosine formula，余弦公式）来获得。当依次分别算出的两两用户间的相关度的时间复杂度：O（N2×D）。D为项目的数量大小，N为用户的数量大小。

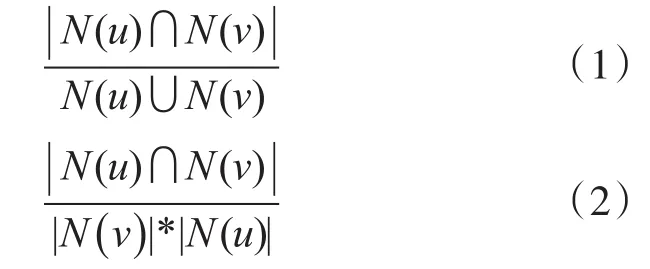
利用式（1）或者式（2）可以得到相似性矩阵。但是在很多项目中此相似性矩阵是十分稀疏的。意味着不少用户两两间没有对相同的项目发生购买行为。如果仅仅只是单纯的把相似性不为零的用户的对数求出，随后只需计算用户对不为零的，这样只会使系统的复杂度升高。利用数组W［a］［b］来存储用户a与b有相同的购买项目行为的数量。首先创建一个倒序排列表。各个项目都记录了发生购买行为的用户信息。然后对每个项目的所有发生过购买行为的用户元组（a，b），W［a］［b］均要加上1。如此就可以只需要用户元组的相似性不为零的数据了。

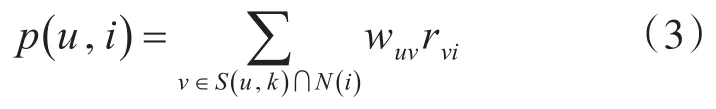
当之前获得相似性矩阵之后，就能使用式（3）来预测项目i能让用户u产生兴趣大小。这里面S（u，k）显示的是用户的相似度最靠近的k个用户的集合，N（i）显示的是对项目i有过购买行为用户的集合。rvi显示用户v对于项目i的兴趣程度的大小，wuv显示的是用户v与用户u的相似性的大小值。

3 基于最大团的协同过滤推荐算法

3.1 社交网络中最大团算法选择

3.1.1 回溯法

Bron-Kerbosch算法［11］是用来计算图的最大团（最大全连通分量，Most significant connected component）的一种算法。其中最基础的一种模型是利用递归与回溯的搜查算法。是一种比较常见的回溯算法。给定3个初始集合（X，R，P）。集合P是包含了全部顶点的集合，而R，X集合初始都为空。依次从集合P中取出一个顶点｛v｝，当集合P中再无顶点时，可能出现以下两种状况：

1）集合R就是最大全连通分量，也就是包含所有最大团成员，同时集合X为空值。

2）无最大团，此时回溯。

针对从各个来自与集合P中的顶点v来说，依次做以下的各项处理：

1）顶点v添加到集合R中，顶点v的邻居顶点组成的集合N｛v｝需与X、P集合相交，这之后循环递归集合（X，P，R）。

2）将集合P中的顶点v删除的同时添加顶点v到集合X中。

只有当集合X与P均为空时，集合R才是最大团的集合。

伪代码过程：

Bron_Kerbosch_1（X，R，P）：

if P and X are both empty：

report R as a maximal clique

for each vertex v in P：

BronKerbosch1（R∪｛v｝，P ∩N（v），X∩N（v））

P=P｛v｝

X=X∪｛v｝

3.1.2 优先分支限界算法

优先分支限界算法一般是按照广度优先或者以最小耗费优先方案搜索问题的解空间树。

算法思想：

1）首先我们假设解空间树已经生成了；

2）解空间树的根结点是初始扩展结点，对于这个特殊的扩展结点，其cn值为0（表示当前团顶点数为0）；

3）首先考察其左儿子结点。在左儿子结点处，将顶点u加入到当前团中，并检查该顶点与当前团中其他顶点之间是否有边相连。当顶点u与当前团中所有顶点之间都有边相连，则相应的左儿子结点是可行结点，将它加入到解空间树中并插入活结点优先队列，否则就不是可行结点；

4）接着继续考察当前扩展结点的右儿子结点。当un＞bestn（bestn表示已经寻找到的团的顶点数，初始值为0）时，右子树中可能含有最优解，此时将右儿子结点加入到解空间树中并插入到活结点优先队列中；

5）继续上述3）和4）步骤直到搜索完整个解空间，算法结束；

6）搜索过程中通过上界un值来截枝避免访问不必要的节点。

3.1.3 最大团算法性能测试与选择

回溯法和分支限界法都是在问题的解空间树T上做搜索策略的算法。一般来说回溯法根据算法设计的不同，求解目标不同，一种是求出符合约束条件的所有解，一种是求出其中一种可行解。若要求出所有解，由于是NP完全问题，耗费一般难以在多项式时间内完成，时间复杂性更接近蛮力穷举法，所以本文中以求出一种可行解为目标。

通过对图的节点与边的扩大，分别对比了蛮力法，回溯法和分支限界法的查找步数来反应算法复杂度。如表1所示：

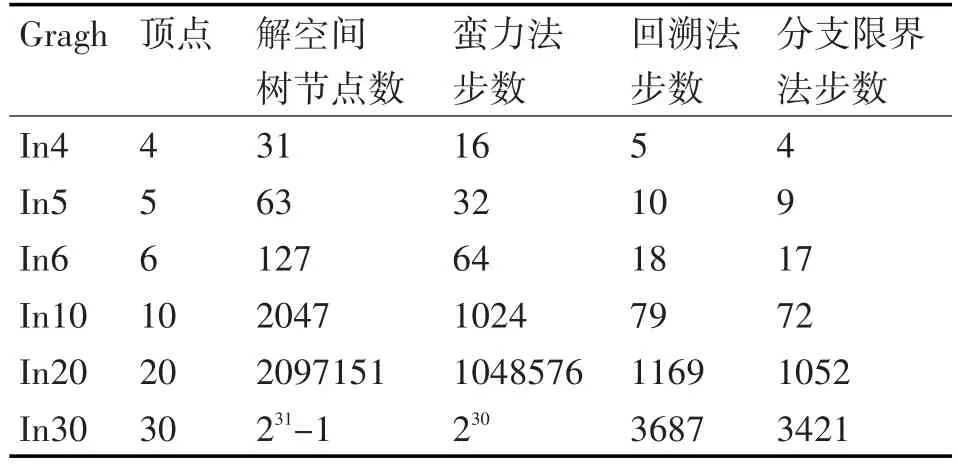
表1 各个最大团算法性能对比

通过表1可知随着顶点的增加，蛮力法的步数几乎呈现几何级增长，而回溯法与分支限界法增长慢了许多，而且分支界限法略好于回溯法。分支限界法的求解目标也是找出满足条件的一个解。在搜索策略上，回溯法沿着深度优先策略搜索问题的解空间树，分支限界法则广度优先或以最大效益优先的方式搜索问题的解空间树。在结点的拓展方式上，回溯法中如果当前结点不能再向深处拓展则判定为死结点，应回溯到最近的活结点，而在分支界定法中，每个活结点只有一次成为拓展结点的机会，一旦放弃不再启用。在空间复杂度上，分支限界法的空间复杂度更高，需要更多的存储空间。

由于分支界限法，并没有显著提升算法的速度，却占用了更多的存储空间。所以综合这些特性，本文选用了回溯法作为最大团算法的基本算法思想。

3.2 基于最大团的协同过滤改进算法

3.2.1 算法基本思想

传统的协同过滤算法理论上是基于社会理论的，因为它们与我们参考其他人的选择的过程类似。而最大团的团成员之间拥有相似的兴趣爱好的可能性的概率理论上比协同过滤算法高。因为根据社会化理论，朋友间的兴趣影响大于社会间不认识的人的兴趣。朋友圈存在着显著的兴趣聚集的趋势。即所谓的“物以类聚，人以群分”。根据此理论，我们设计基于最大团的协同过滤改进算法。

这个理论核心思想是：对于传统的协同过滤，存在最大团关系的成员的推荐值由团成员的协同过滤值的均值决定，而不是原来协同过滤值。这样减少了某些协同过滤的极端值对协同过滤值准确性的影响，而且对于那些缺少数据的成员，也可以通过团成员的均值来对其确定推荐值，这样减少了冷启动率，增加了推荐效率。

算法步骤：

1）利用Born-Kerbosch算法算出网络中包括的所有节点数大于2的最大团。

2）利用协同过滤算法算出网络中包括的所有节点的协同过滤值。

3）通过对各个最大团团成员之间协同过滤值求均值，作为团推荐值。将团推荐值作为用户推荐值推荐给团员。

4）当有用户同时在多个团中时，在不考虑各个团的权重的情况下，将多个团推荐值求均值。将团推荐值作为用户推荐值推荐给团员。

5）不在最大团的成员，则将原始计算的协同过滤值作为推荐值推荐给用户。

3.2.2 算法示例

如图1，以用户A为中心的社交网络图中，包括2个最大团：团1（A，E，F）与团2（A，B，C）。

图1 用户A的社交网络图

首先利用协同过滤算法求出用户的推荐值的集合W（表2），利用Born-Kerbosch算法算出网络中包括的所有节点数大于2的最大团，图1中的最大团为团1（A，E，F）与团2（A，B，C）。

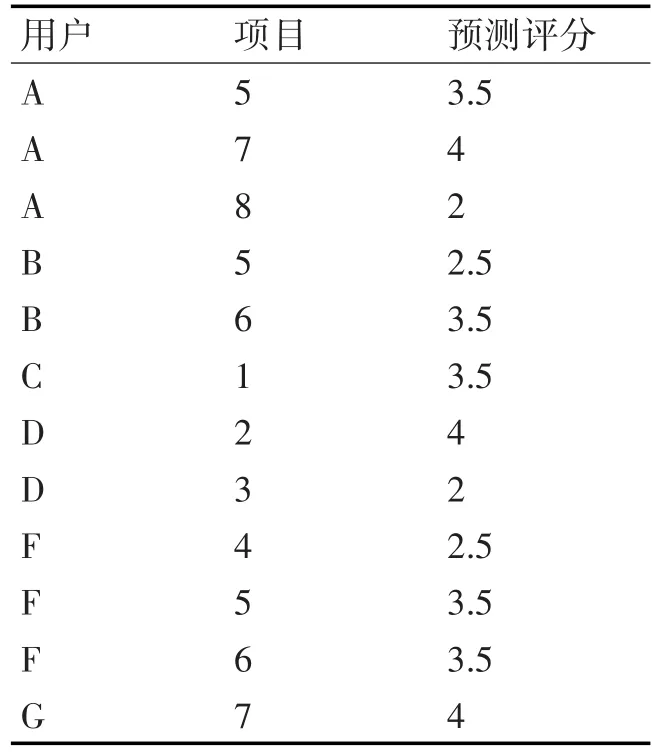
表2 为用户A的社交网络图的部分协同推荐值

表3为团成员对所有项目评分的均值。

表3 团1与团2的集体推荐值

当有用户同时在多个团中时（如A），在不考虑各个团的权重的情况下，将多个团推荐值求均值。将团推荐值作为用户推荐值推荐给团员。最后将团推荐值与未出现在最大团中的成员的协同过滤推荐值放入集合F，作为最终的推荐值返回推荐给用户。其中图3为社交网络图的算法流程图。

4 实验结果及分析

4.1 数据集

Yelp网站是美国最著名的评论网站之一，Yelp数据集来源于Yelp举办的“Yelp数据集挑战赛”的第八轮［12］。本文涉及到的部分Yelp数据集包括客户对店铺的评分和好友关系。数据量大约为400M。

4.2 评价标准

均方误差（Mean Squared Error，MSE）：用于预测业务分析和供应链管理准确性的最常用措施之一。实际观察值与预测值之间的平均值是平均值。误差的平方往往会大大加重统计学异常值，影响结果的准确性。

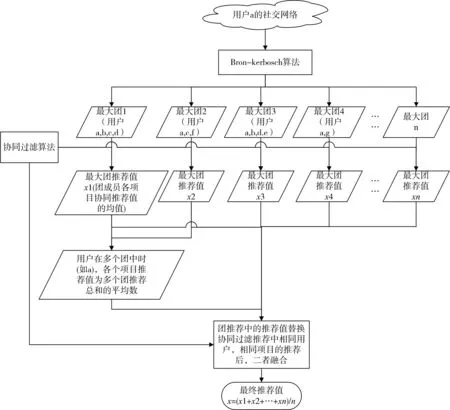
图2 社交网络图的算法流程图

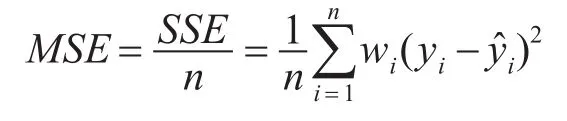
K-平均准确率（Average Precision at Kmetric，MAPK）［14］：K的平均精度是数据集中所有实例的K（APK）度量的平均精度的平均值。经常被使用的一种用于信息检索的指标是APK。APK是对一组响应查询提交的top-k文档的平均相关性分数的量度。在APK的指标当中，结果集的顺序位置对结果有很大的影响，因为如果结果文档都相关且相关文档在结果中显示较高，则APK分数会更高。因此，这是推荐系统的良好指标。

推荐率（Recommendation rate，RA）：推荐率来描述被推荐用户占总用户的比率。

推荐率=被推荐用户/总用户数

冷启动率［15］（Cold start rate，CSB）：冷启动率来描述未被推荐用户占总用户的比率。

冷启动率=未被推荐用户/总用户

ROC曲线［16］：又称感受性曲线，是一种标准技术，用于在真阳性（TP）和假阳性（FP）错误率之间的一系列权衡范围内总结分类器性能。ROC曲线是灵敏度（模型预测事件的能力正确）与可能的截止分类概率值π0的1特异性的关系曲线。

4.3 YELP数据集实验结果分析

实验一：算法的有效性对比

表4是两种算法在YELP数据集中测试的效果。总体而言，无论是推荐率，推荐的准确率都有提升。而且对于传统推荐系统中比较严重的冷启动问题也得到了一定程度的缓解。

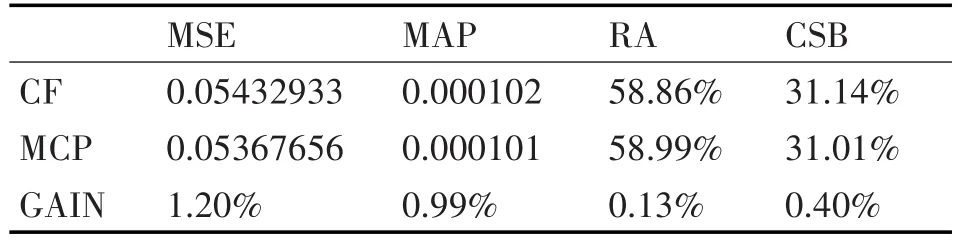
表4 最终实验数据及对比

实验二：算法敏感性和特异性

图3为2个算法的ROC曲线图。ROC曲线图对连续的变量设计多个不相同的阈值，依次算出多个感性度和异常度，再以（1-异常性）为横坐标、感性度为纵坐标勾画成曲线图。图中最大团算法曲线的阴影面积更大，显示评测的准确度更高。敏感性和特异性均较高的临界值的点均分布在曲线的最靠近坐标图左上方，显示最大团无论是敏感性还是特异性均变现的比传统的协同过滤算法优秀。

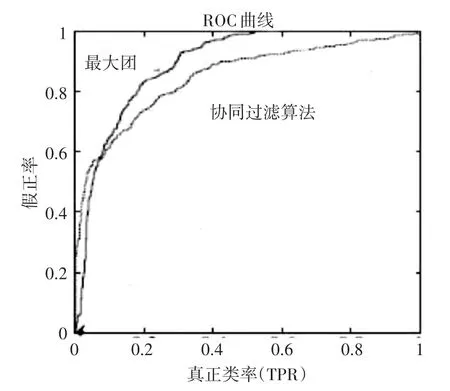
图3 ROC曲线图

实验三：算法性能测试

图4利用逻辑回归来刻画Precision与Recall之间的关系。由图可知最大团正确率与召回率更高，而且正确率与召回率更加均衡。

图4 Precision与Recall逻辑回归图

由上述实验结果可知：

提出的基于最大团的协同过滤算法在无论是推荐率，推荐的准确率都有提升，而且对于传统推荐系统中比较严重的冷启动问题也得到了一定程度的缓解。

5 结语

基于最大团的协同过滤算法，融合传统的协同过滤与社交网络关系来进行推荐，无论在推荐率，推荐的准确率都有提升。由于利用了社团的关系推荐，冷启动问题也得到了一定程度的缓解。但是由于社会关系数据比较少，最大团算法的提升效率并不大，而且对于团并未进行侧重分析，设置必要的权重，这也让精度提升的并不明显，这是将来可以进一步改进和探索的方向。