一种改进油田产量预测算法的研究∗

张 旭 谷尚震 刘卫华

（1.重庆科技学院石油与天然气工程学院 重庆 401331）（2.中国石油塔里木分公司 库尔勒 841000）

1 引言

数据准确的油田产量预测对科学制定采油计划，对油田开发现状进行科学评价具有重要意义，是油田开发决策的重要数据支撑。影响油田产量的因素众多，井网密度、注水压力、采出速度、产量递减率、综合含水率等都对油井产量构成影响。这些影响油田产量的众多因素之间构成了一个极其复杂的非线性系统，采取传统的方法难以准确预测油田的产量。

文献［1］采用多元回归算法和自回归模型对油田产量进行预测，由于这种算法是基于线性模型而构建的，因此面对影响油田产量中的众多非线性因素预测的准确度难以保证。文献［3］利用威布尔预测模型算法、双对数算法、灰色系统模型算法、俞启泰模型算法以及微分模拟算法等5种非线性迭代算法对低渗透油田进行产量预测，结果显示这些模型的预测结果都具有一定局限性，对不同的地质条件其预测结果的准确度相差较大。文献［4］运用BP神经网络的智能算法对油田产量进行预测，具有算法简单、仿真能力强、易于实现的优点，但是在实际运行中表现出了容易陷入局部最优、收敛时间长的缺陷，降低了该算法的实用性。

针对上述算法存在问题，本文提出一种改进油田产量预测算法，该算法利用自适应的权值调整算子优化BP神经网络连接权值和阈值，提高神经网络的收敛速度，提升产量预测的精度。

2 BP网络算法

BP网络是一种单向多层次前馈网络，采用误差反向传播算法调整网络的连接权值等参数。BP网络按照其网络单元功能的不同可分为输入层、中间层以及输出层。输入层，其典型结构如图1所示。

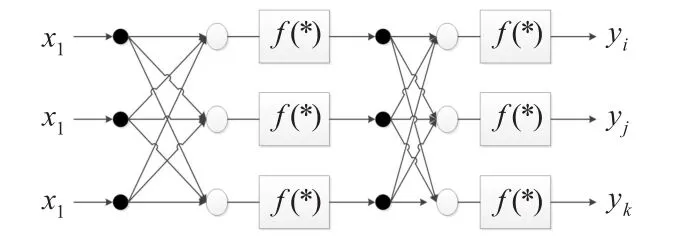
图1 BP神经网络典型结构图

图1所示的BP网络的输入向量为 X={x1，x2，x3，…xn}T，则从输入层至中间层的权向量为Vk={xk1，xk2，xk3，…xkn} ，中间层的权值是 V={x1，x2，x，…x}T。中间层的输入为3m中间层的输出为 Z={z1，z2，z3，…，zm}Z。中间层到输出层第i个节点的权向量为Wim}T，中间层至输出层的连接权值矩阵为W={w1，w2，w3，…，wn}T。输出层的输入为 S={s1，s2，s3，…，sn}T，BP网络的输出向量为

BP网络预测算法主要由学习算法和预测算法组成。学习算法是通过对样本数据进行自主学习确定网络各层之间连接权值和各个神经单元的阈值；预测算法则是利用学习成熟的网络对未知数据进行模拟预测，得出预测结果。在BP网络学习算法中，学习过程有样本数据的正向传递和误差数据反向传递两个过程。输入样本由输入层传入网络，经由中间层逐层解析，传递至输出层。如果输出层的输出与样本输出存在偏差，则将偏差反置通过中间层向输入层反向传递，在传递过程中将偏差信号分别作用到中间层的各个神经单元，修正各个网络单元的连接权值。如此不断重复，直到输出层的输出与期望数据相符为止，此时BP网络的参数也调整至最佳。

如果BP网络的学习样本数为K，则需要学习的样本对为（X1，P1），（X2，P2），…，（XK，PK）。由于 BP网络每次学习和参数修正是针对单个样本的优化，而对其他样本可能存在输出偏差增大的情况，因此需要将样本成批的学习而不是单个样本的反复学习。最后通过成批样本学习得出的BP网络输出总偏差定义为

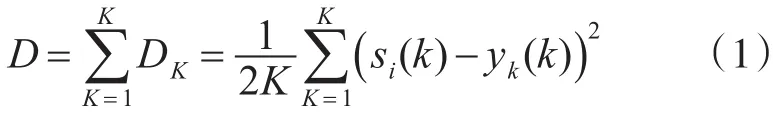
BP网络算法流程如图2所示。

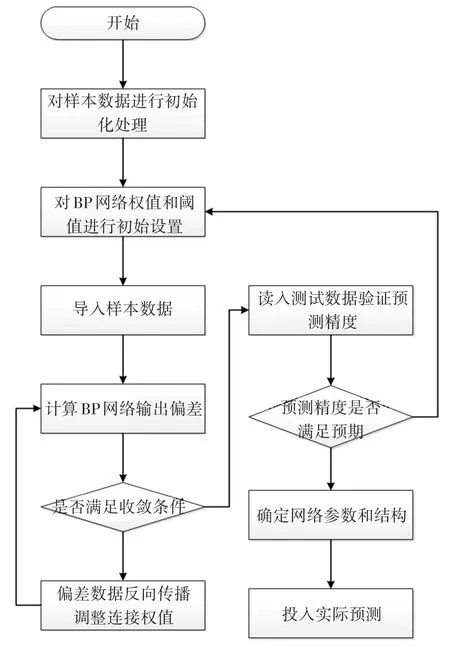
图2 BP网络的算法流程

3 BP网络算法的改进

BP网络算法的学习过程是一个非线性梯度最优的过程，在学习样本数据不足的前提下收敛过程容易出现局部最优。BP网络算法在学习过程中其参数收敛速度受到学习率等因素影响并不理想。为此文本在引入自适应的权值调整算子，对BP网络每次想学习过程中的权值调整进行优化，把单一方向的调整变成双方向调整，同时通过自适应选择梯度下降法和高斯牛顿法来优化网络权值，从而提高权值参数的收敛速度，同时避免出现局部最优现象。

优化的权值调整算子采用非线性最小二乘法构建，其数学表达式为

式（2）中G是偏差对权值微分的一阶偏导数矩阵。μ是标量系数，当μ变大时该权值调整算法接近于梯度下降法，当μ变小接近0时该权值调整算法接近于高斯牛顿算法。因此权值调整算子随着系数μ的变化，表现出不同的特性。权值调整算法的具体步骤描述如下。

1）将输入样本导入BP网络的输入层，利用式（3）计算出输出值。

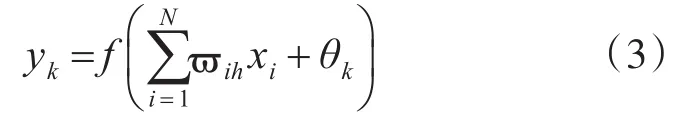
然后运用式（1）计算出所有样本的累计偏差。

2）利用式（4）计算累计偏差对权值微分的一阶偏导数矩阵。

式（4）中E是对第m层输入的第i个元素变化的敏感度，n为单层中间层的权值代数和。

基于权值调整算子的改进BP预测算法改进了传统的BP预测算法的误差反馈函数，使得算法收敛时间得到有效控制，迭代次数减少，同时权值调整算子的介入使得BP学习过程摆脱了可能存在的局部最优桎梏，算法精度得到保证。

4 算例验证

算例的预测算法的样本数据来自大庆油田A采油厂近6年的所有油井日采油速度和日产量。其中前5年的数据作为学习数据库，最后一年的数据作为测试数据库。预测算法的模型如下式：

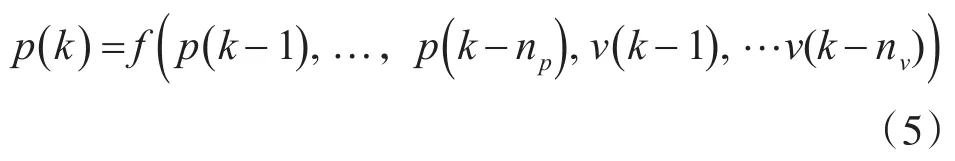
式（5）中p（k）表示石油产量，v（k）表示采油速度。n值取20，nv值取20，即以20天的石油日产量和采油速度为输人样本，以的石油日产量为期望输出，用预测算法模型建立两者之间的非线性函数关系。由于油井产量是一个复杂的非线性系统，影响因素众多，因此日产量变化范围大，并且输入的样本数据量纲不同，所以使用Matlab中的prestd函数对BP预测函数的学习样本数据集合进行预处理，使学习样本的数值在0～1之间。

根据BP网络理论，三层BP网络能够以较高的精度拟合大多数非线性函数，因此选择三层网络结构作为预测算法模型的基础。样本输入数量为20，三层BP网络的输人节点为20个，中间层节点数量设定为80，输出节点为1。因此本三层网络模型结构为（20，80，1），中间层函数采用tansig函数，输出层则采用purelin函数。

改进产量预测算法的收敛情况如图3所示，算法的最小的偏差平方为774607*10-3，算法完成收敛的期望偏差为0.01。图3横坐标为迭代次数，纵坐标为期望输出偏差，当输出偏差小于期望值时，算法收敛完成。由图2知，通过13769次收敛，算法完成收敛。

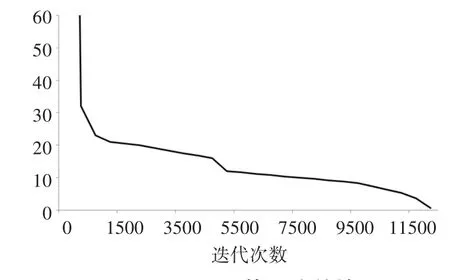
图3 改进预测算法收敛情况

预测模型的预测结果情况如图4所示。从图4中可以看出预测结果平均精度约为94.8%。

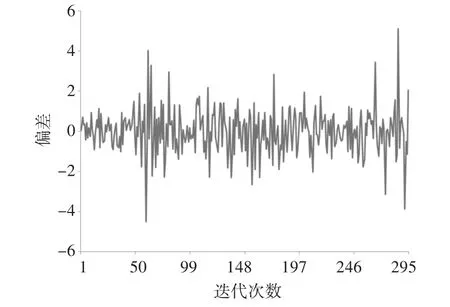
图4 改进预测算法的预测结果偏差

与传统BP网络预测算法的预测性能对比如表1所示。

表1 改进预测算法与传统BP网络算法的性能对比

由表1可以看出改进预测算法叫传统BP网络算法具有更好的预测精度和更快的收敛速度。

5 结语

针对传统油田产量预测算法难以计算影响油田产量的非线性变量以及BP网络算法存在的收敛慢、精度欠缺的问题，本文提出了一种基于BP网络算法的改进油田产量预测算法。该算法通过自适应的权值调整算子对BP网络权值的优化调整加快预测算法的学习速度，并使得算法摆脱局部最优的缺陷，提高算法的预测精度，最后通过算例验证了改进算法的有效性，同时得出以下结论：1）基于三层网络结构的传统的BP网络算法能够较为实际地反馈油田产量和各个影响因素之间的非线性关系，在充分收敛的情况下具有一定的油田产量预测性能，但是由于收敛速度过慢切在学习数据不足的情况下容易陷入局部最优；2）对传统BP网络算法的初始连接权值进行优化调整能够较为明显地提高算法地收敛性能；3）本文在算例验证中对油井各种影响产量地开采因素考虑较为局限，没有针对同一储层地油井之间地产量影响以及前期开采累计量地影响进行充分考虑，因此需要在进一步加以研究，以继续提升算法的预测准确度。