双分数Vasicek利率环境下脆弱期权定价∗

王瑶 薛红

（西安工程大学理学院 西安 710048）

1 引言

随着社会的不断发展，出现了多种新型期权，脆弱期权就是一种含有信用风险的期权。文献［1］以Lévy过程为基础，给出了模糊环境下脆弱看涨期权定价公式。文献［2］采用偏微分方程法推导出脆弱期权定价公式，并利用有限差分法给出其数值解。文献［3］在随机波动率情况下，利用 Itô引理推导出无违约风险的脆弱期权期权所满足的偏微分方程。文献［4］在随机利率的情况下，利用保险精算方法得到分数布朗运动环境下脆弱期权定价公式。文献［5］利用Itô引理和等价鞅测度变换法得到多跳-扩散环境下脆弱期权的解析解。文献［6］应用风险中性定价方法得到分数-跳扩散环境下欧式脆弱期权定价公式。文献［7］借助信用风险模型，利用保险精算方法获得分数跳-扩散环境下脆弱期权的定价公式。近年来，不少学者提出了双分数布朗运动，它是更具一般的高斯过程。文献［8］讨论了双分数布朗运动在不同参数H，K下的积分理论，并给出了双分数布朗运动环境下Itô公式。文献［9］给出了双分数Brown运动环境下的股本权证定价公式。文献［10～12］是有关双分数环境下的期权定价，文献［13～14］利用保险精算方法给出了双分数-跳扩散环境下再装期权定价公式。有关双分数Vasicek利率环境下期权的定价问题可参考文献［15～17］。因此，本文假设股票价格、公司价值和公司负债均服从双分数Brown驱动的随机微分方程，在双分数驱动的Vasicek利率情况下，运用保险精算方法得到双分数Vasicek利率环境下脆弱期权定价公式。

2 金融市场数学模型

假设股票价格为 S（t），公司价值为V（t），公司负债为D（t），设在T时刻公司承诺支付给债权人的金额为 X（T），若公司具有清偿能力，则在T时刻公司的债权人取得的偿付额为 X（T）。若在T时刻V（T）＜D（T），则发生违约，此时公司的债权人取得的偿付额就是 Xd（T）=，则在T 时刻，公司的实际支付额可以表示为

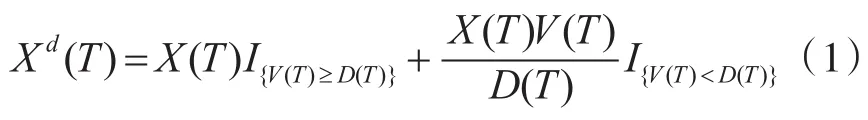
假定股票价格 S（t）、公司价值V（t）、公司负债D（t）和短期利率分别满足如下随机微分方程［9］：

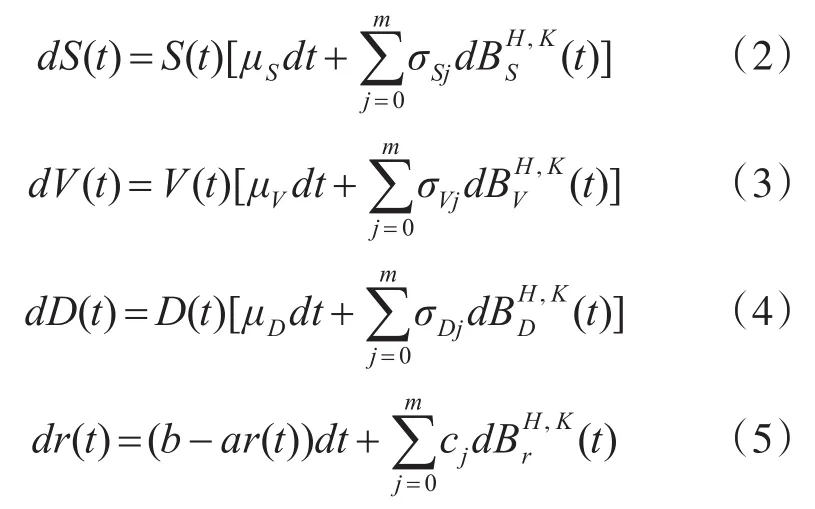
其 中 ，μS，μV，μD，σSj＞0，σVj＞0，σDj＞0（j=1，2，…，m），是 完 备 概 率 空 间（Ω，F，P）上相互独立的双分数布朗运动。

引理 1［15，18］随机微分方程（2）、（3）、（4）、（5）的解分别为

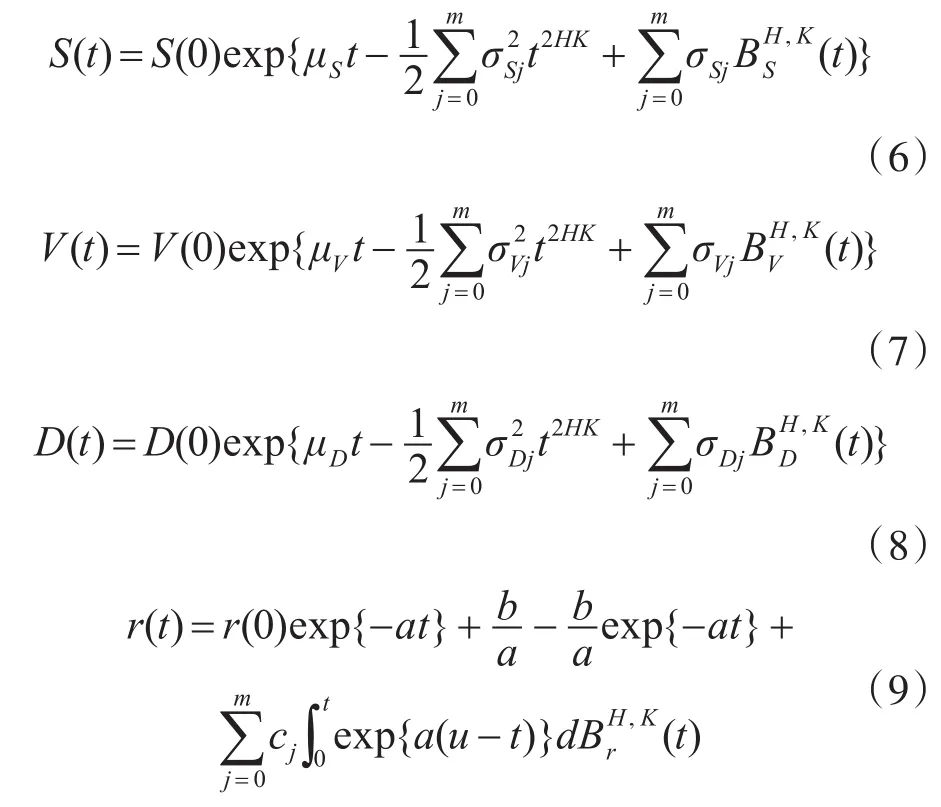
定义1［7］股票价格过程{S（t），t≥ 0}在 [t，T]上的期望回报率 βS（u），u∈[t，T]定义为

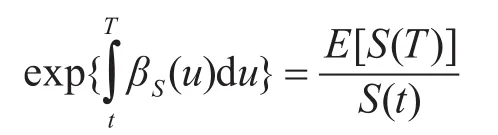
引理 2［7］随机过程 {S（t），t≥ 0} 、公司价值{V（t），t≥0} 和公司负债 {D（t），t≥0}[0，T]上的期望回报率分别满足 βS（u）=μS，βV（u）=μV，βD（u）=μD。

引理3［15］设随机变量 ξ1～N（0，1），ξ2～N（0，1），相关系数 cov（ξ1，ξ2）=ρ，当 a，b，c，d，k 为实数时，有

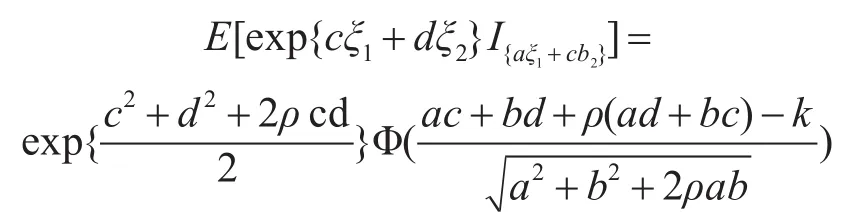
定义2［19］在到期日T时刻，承诺支付额为X（T）=（S（T）-Q）+而出现违约或破产时的实际支付额为 X（T）=的脆弱看涨期权的保险精算价格定义为

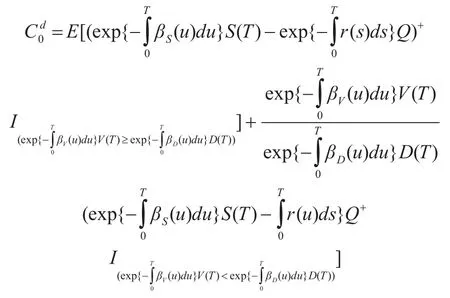
3 脆弱期权的定价

定理1 在到期日T时刻，承诺支付额为X（T）=（S（T）-Q）+而出现违约或破产时的实际支付额为 X（T）=的脆弱看涨期权的保险精算价格为

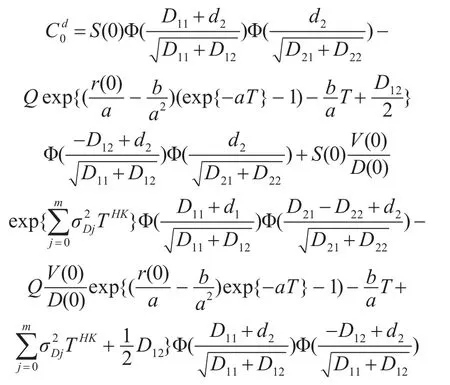
其中

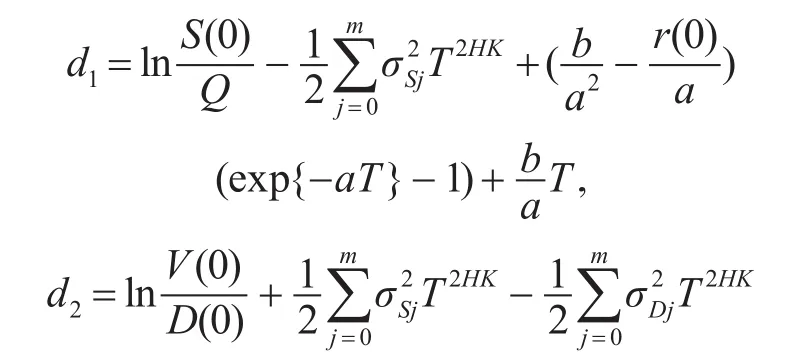
证明

令A1=

则

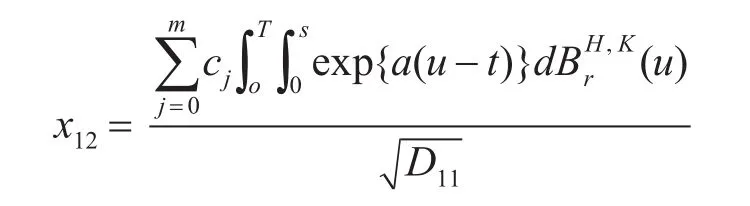
即A1=

令

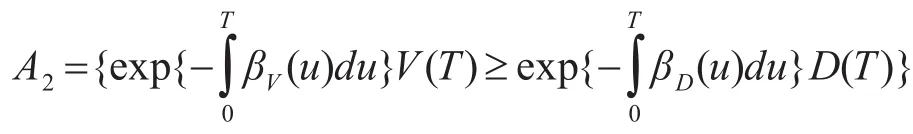
则

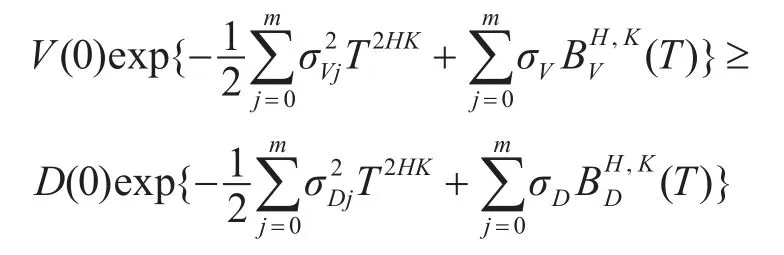
记 D21=

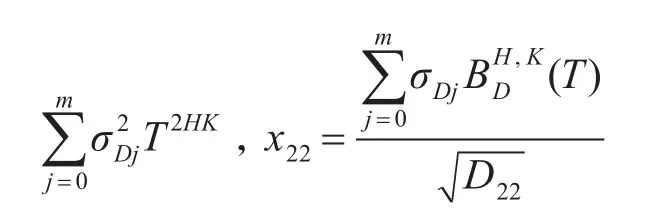
则A2=

从而

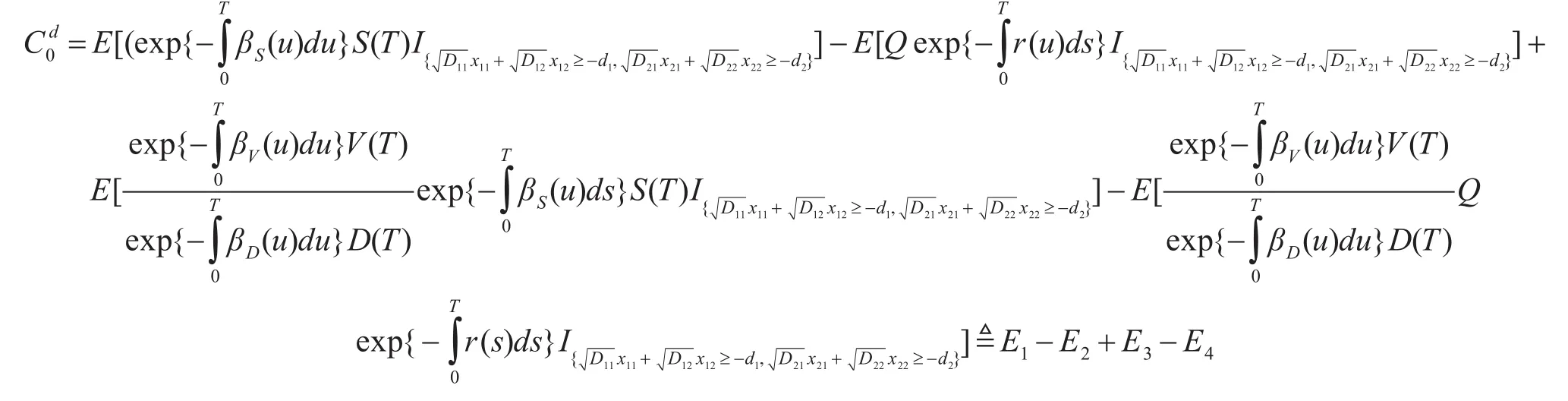
其中

推论当K=1时，可得分数布朗运动环境下具有随机利率的欧式脆弱期权定价公式。特别地，当 b=0，c=0，a→0且 σD→0时，可得分数布朗运动环境下脆弱期权定价公式（见文献［20］）。

4 结语

本文假设利率满足双分数Vasicek利率模型，借助双分数布朗运动随机分析理论，利用保险精算方法推导出脆弱期权的定价公式，特别地，当K=1时，得到分数布朗运动环境下具有随机利率的的欧式脆弱期权定价公式。