强震作用下巨型网格结构的抗倒塌性能研究

李 峰，王泽菡，宁尧尧

(西安建筑科技大学 土木工程学院，陕西 西安710055)

随着科技的进步以及人们对空间需求的不断增大，当代建筑的结构形式趋向于超高层、大跨度等方面发展.新型的空间网格结构由于能够满足大跨度的要求，同时还具有受力合理、自重较轻等优点成为大跨度结构中的主要形式[1].

空间巨型网格结构由主体结构和子结构组成.其中主体结构由拱向与纵向立体桁架交叉而成的大网格，承担整个结构上的荷载并将其传递至支撑结构；子结构可采用单层或双层普通网壳结构，布置于主体结构的大网格中，承担大网格范围内的屋面载荷并将它们传递至主体结构，从而形成大网格套小网格的一种结构形式[2].圆柱面巨型网格结构传力路线明确、形式多样、施工方便，是一种较为理想的巨型网格形式.

目前，国内外针对框架结构连续性倒塌事故的研究已比较成熟，形成了统一的设计思想和相应的规范[3-7].但针对大跨度空间结构连续性倒塌的研究尚处于起步阶段.因此，本文从定量的角度研究圆柱面巨型网格结构的倒塌性能和节点刚度对结构抗倒塌性能的影响.从而为圆柱面巨型网格结构抗连续倒塌设计提供参考.

1 倒塌分析方法与结构计算模型

采用有限元ANSYS/LS-DYNA分析软件建立圆柱面巨型网格结构模型，通过输入一系列经过调幅的地震波对圆柱面巨型网格结构进行倒塌仿真分析，得到结构倒塌时的临界荷载和失效模式.

1.1 倒塌分析方法

采用增量动力分析法对圆柱面巨型网格结构进行强震作用下倒塌性能的研究.增量动力分析法(Incremental Dynamic Analysis，简称IDA法)是通过对一条地震动记录(或多条地震动记录)递增式地调整其强度幅值，生成一组或多组具有递增强度的地震动记录，针对每一强度的地震动记录进行一次非线性动力时程分析，直至结构倒塌.将地震动的强度参数与其对应的结构反应参数形成的一系列点连接起来的曲线，称为“IDA曲线”.通过曲线可以确定结构的抗震需求或抗震能力[8].

1.2 结构计算模型

通过初步静力计算设计，圆柱面巨型网格结构采用跨度S为90 m，大网格数为6×6，矢跨比为1/6，立体桁架梁高度h1为3.0 m，纵向立体桁架梁高度h2为2.9 m，梁段内网格数n为7.主体结构采用倒放四角锥形式，且在四角锥底面布置对角撑杆即斜杆以保证构件内部几何不变，主体结构以纵向两端上下弦固定铰支于支承结构上，结构布置如下图1所示.结构的构件均采用圆钢管，屈服强度为345 MPa.杆件截面为Φ180×10.

图1 圆柱面巨型网格结构Fig.1 Cylindrical reticulated mega-structure

钢材的本构关系采用塑性随动强化模型，该模型与应变率相关，可以考虑杆件失效，是各向同性、随动硬化或各向同性和随动硬化的混合模型.通过调整硬化参数β来控制硬化状态，若β=0，则表示仅随动硬化；若β=1，表示仅各向同性硬化；若0<β<1，则表示混合硬化模型.应变率用Cowper-Symonds模型来考虑，用与应变率有关的因数表示屈服应力[9]：

(1)

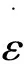
(2)

选取的本构模型中应变率参数C、P取为零，材料的失效应变为0.05，切线模量取为6.1×103MPa，应力-应变关系图如图2所示.

图2 强化模型应力-应变关系图Fig.2 Stress-strain of the strengthened model

根据《建筑结构荷载规范》(GB50009-2012)[10]选取结构的设计荷载：屋面恒载为800 N/m2，屋面活载为500 N/m2，雪荷载为350 N/m2，按荷载效应组合计算出设计荷载为975 N/m2.

2 倒塌破坏模式及机理的研究

2.1 三向地震作用

选取El Centro波[11]，对圆柱面巨型网格结构在三向地震作用下进行倒塌破坏分析.以8度罕遇地震下的地震波为调幅基础，其峰值加速度为4 m/s2(即400 Gal).利用hunt&fill算法[12]对地震波的峰值加速度PGA进行调幅，调幅步长取2.0 m/s2，步长增量为0.1 m/s2.IDA曲线中选取峰值加速度PGA作为地震动强度参数IM，结构最大节点位移和结构失效杆件的数量作为结构响应参数DM.

将经过地震波调幅后的有效分析结果的峰值加速度和结构响应绘制于表1.从表中可以看出圆柱面巨型网格结构在峰值加速度达到20.10 m/s2时结构杆件出现失效，节点最大位移为1.08 m.

表1 结构响应

从地震的时程响应可以看出结构在强震作用下的全过程响应，如图3所示.对比结构的位移-时间曲线和速度-时间曲线可以看出，当峰值加速度达到22.80 m/s2时，结构节点的最大位移在11.82 s时偏离了平衡位置，但随后又保持稳定振动.当峰值加速度达到23.11 m/s2时，在16.62 s时结构的最大节点位移发散，位移最大值为11.97 m.由速度-时间曲线可知，节点速度在16.62 s时偏离平衡位置，不再围绕原点振动.因此，尽管节点位移未达到15 m，但是位移后续也不可能趋于稳定.则判定结构发生倒塌破坏的极限峰值加速度为23.11 m/s2.

图3 地震时程响应Fig.3 Earthquake time response

从节点位移IDA曲线和结构失效杆件数量IDA曲线，即图4所示，同样可以看出结构在峰值加速度达到23.11 m/s2时，结构的位移开始发散，杆件数量急剧增大.因此可以将峰值加速度为23.11 m/s2作为结构的极限荷载.

图4 三向地震作用下的IDA曲线Fig.4 The IDA curve under action of three earthquakes

通过结构在极限荷载作用下圆柱面巨型网格结构的变形图及失效杆件分布图可以看出结构在倒塌破坏时的破坏模态和失效杆件分布区域，如图5所示.从(a)图中可以看出圆柱面巨型网格结构的屈曲现象为拱向桁架和纵向桁架均发生了较大的平行位移，越靠近结构中心节点位移越大；纵向桁架与拱向桁架均发生了以结构顶点为中心的下凹屈曲.图(b)中可以看出结构整体的失效杆件主要分布在支座处，且失效杆件往结构中间发展，尤其是位于纵向桁架与拱向桁架相交节点处.

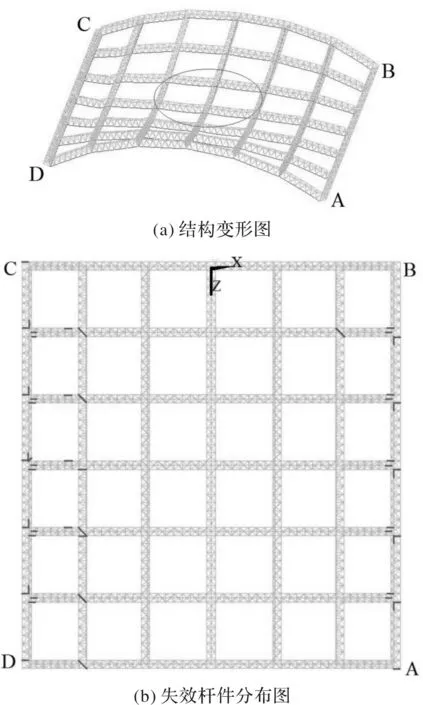
图5 峰值加速度为23.11 m/s2时结构变形图和失效杆分布图Fig.5 Frame deformation and failure rod distribution with pake acceleration at 23.11 m/s2 time

分析峰值加速度为23.11 m/s2时结构中最先失效单元3 327的应变时程曲线，如图6所示.从图中可以看出单元的最大应变为0.041未达到材料的失效应变.对比图5中失效杆件的数量可知，失效杆件的数量仅占整体结构杆件数量的0.98%(即56/5 733)，因此认为结构在强震作用下的倒塌是由几何非线性引起的动力失稳.

图6 单元3327的应变时程曲线图Fig.6 The time path of element 3 327

2.2 加强模型在三向地震作用下

根据上节的分析结果可知，在El Centro波三向作用下对于圆柱面巨型网格结构的倒塌破坏是先从支座处节点的弦杆发生失效.为了避免由于支座杆件设计的不合理而导致结构倒塌，在下面分析中加强支座处杆件规格.取支座节点处杆件为Φ203×10，如图7所示，分析结构在强震作用下的倒塌性能.

图7 加强模型示意图Fig.7 The strengthened model

将经过地震调幅后有效分析结果的峰值加速度和结构响应绘制于表2.从表中可以看出圆柱面巨型网格结构在峰值加速度达到20.10 m/s2时结构杆件出现失效，节点最大位移为1.15 m.

表2 结构响应

对比结构的位移-时间曲线和速度-时间曲线，如图8所示，可以看出，加强后的模型当峰值加速度达到24.9 m/s2时，结构的最大节点位移直接在15.82 s发生发散，位移最大值为7.61 m.由速度-时间曲线可知，此时速度也偏离平衡位置，不再围绕原点振动.因此判定结构发生倒塌破坏的极限峰值加速度为24.9 m/s2.对比原结构模型位移变化过程可知，原模型发生破坏之前位移发生了两次突中间有一段处于稳定的状态，而加强后的模型位移直接迅速增大.由此可知虽然加强后的模型极限荷载提高了但结构的延性降低.

图8 地震时程响应Fig.8 Earthquake time response

加强后的圆柱面矩形网格结构经过调幅分析后，将结构响应与原模型的结构响应绘制于同一坐标系中进行对比分析，如图9所示.从图中可以看出，加强后的圆柱面巨型网格结构的IDA曲线的变化趋势相同，但是加强后的拐点推迟，即倒塌临界荷载增大到24.9 m/s2.临界荷载比原模型结构提高了7.7%.

图9 三向地震作用下的IDA曲线Fig.9 The IDA curve under action of three earthquakes

对比加强后临界荷载作用下结构的变形图和失效杆件分布图，如图10所示.从图(a)可以看出加强后的变形图不同于原模型，而呈现出拱向桁架与第二纵向桁架相交处出现凹陷现象.失效杆件从第二纵向桁架与拱向桁架相交节点处开始，杆件失效的扩展路径是向已破坏节点周围延伸.由此可见，加强模型破坏时与原结构破坏方式相同均是位移和失效杆件突然发散导致结构倒塌.因此加强后的圆柱面巨型网格结构仍为由几何非线性引起的动力失稳倒塌.

图10 峰值加速度为24.90 m/s2时加强模型变形图和失效杆件分布图Fig.10 Frame deformation and failure rod distribution with peak acceleration at 24.90 m/s2 time

3 节点刚度对倒塌性能的研究

采用梁单元建模可在ANSYS有限元建模中实现结构刚接，结构单元类型采用BEAM161单元.将地震调幅后的有效分析的峰值加速度和结构响应绘制于表3.从表中可以看出圆柱面巨型网格结构在峰值加速度达到15.00 m/s2时结构中出现失效杆件，最大节点位移为0.249 m.

表3 结构响应

提取有效分析结果的位移-时间曲线和速度-时间曲线，如图11所示.从图中可以看出，当峰值加速度达到25.60 m/s2时结构的节点位移发散.对比速度-时间曲线可知，节点速度也偏离了平衡位置.因此判定结构发生倒塌破坏的极限峰值加速度为25.60 m/s2.

对比圆柱面巨型网格结构在节点刚接和铰接两种情况下的IDA曲线，如图12所示.从图中可以看出不管节点为刚接还是铰接圆柱面巨型网格结构的IDA曲线的变化趋势相同，但是节点为刚接时曲线的拐点推迟，即倒塌临界荷载增大到25.60 m/s2.临界荷载比节点铰接时提高了12.78%.

图11 地震时程响应Fig.11 Earthquake time response

图12 在三向地震作用下的IDA曲线Fig.12 The IDA curve under action of three earthquakes

节点刚接时临界荷载作用下结构的变形图和失效杆件分布图，如图13所示.从图(a)可以看出节点刚接的变形图不同于节点铰接的变形图，节点刚接的变形图中与纵向边桁架相连的拱向桁架杆件出现了消失，由于杆件失效，ANSYS/LS-DYNA软件将其剔除.因此结构杆件刚接时，失效杆件首先发生在纵向边桁架与拱向桁架相交处.而结构整体变形未出现凹陷.失效杆件的扩展路径是向结构中心延伸.节点刚接模型破坏与节点铰接模型破坏均是位移和失效杆件突然发散导致的.因此节点刚接的圆柱面巨型网格结构与节点铰接的倒塌破坏均是由几何非线性引起的动力失稳.

图13 峰值加速度为25.60 m/s2时结构变形图和失效杆件分布图Fig.13 Frame deformation and failure rod distribution with peak acceleration at 25.60 m/s2 time

4 结论

(1)圆柱面巨型网格结构在强震作用下的倒塌是由几何非线性引起的动力失稳，即在结构倒塌时几何非线性的作用明显强于结构塑性发展导致的强度破坏，但是在结构倒塌过程中也伴随着强度破坏.

(2)在El Centro波三向作用下，圆柱面巨型网格结构发生倒塌破坏时，支座处杆件最先发生失效，然后失效杆件向周围扩展.在扩展过程中，主要为纵向与拱向桁架相交处网格的杆件发生失效.加强支座杆件后结构的抗倒塌能力比原结构模型提高了7.7%，但结构的延性降低了.加强后结构倒塌时最先失效的杆件是与支座相邻的拱向与纵向桁架相交处的杆件.

(3)节点为刚接时圆柱面巨型网格结构结构的倒塌破坏仍为失稳破坏，结构的抗倒塌能力比节点铰接时提高了12.78%，不算太大，为了考虑施工方便，因此按照铰接节点设计是偏保守且合理的.